7.E: Electricity (Exercise)
- Page ID
- 101249
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
10.1: Static Electricity and Charge- Conservation of Charge
1. There are very large numbers of charged particles in most objects. Why, then, don’t most objects exhibit static electricity?
2. Why do most objects tend to contain nearly equal numbers of positive and negative charges?
10.2: Coulomb’s Law
3. Figure \(\PageIndex{1}\) shows the charge distribution in a water molecule, which is called a polar molecule because it has an inherent separation of charge. Given water’s polar character, explain what effect humidity has on removing excess charge from objects.
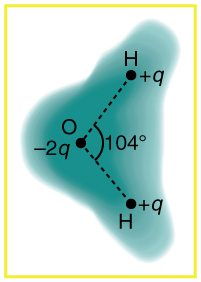
4. Using Figure \(\PageIndex{1}\), explain, in terms of Coulomb’s law, why a polar molecule (such as in Figure \(\PageIndex{1}\)) is attracted by both positive and negative charges.
5. Given the polar character of water molecules, explain how ions in the air form nucleation centers for rain droplets.
10.3: Electric Field- Concept of a Field Revisited
6. Why must the test charge \(q\) in the definition of the electric field be vanishingly small?
7. Are the direction and magnitude of the Coulomb force unique at a given point in space? What about the electric field?
10.4: Electric Field Lines
8. Compare and contrast the Coulomb force field and the electric field. To do this, make a list of five properties for the Coulomb force field analogous to the five properties listed for electric field lines. Compare each item in your list of Coulomb force field properties with those of the electric field—are they the same or different? (For example, electric field lines cannot cross. Is the same true for Coulomb field lines?)
10.5: Electric Potential and Potential Energy
9. Voltage is the common word for potential difference. Which term is more descriptive, voltage or potential difference?
10. If the voltage between two points is zero, can a test charge be moved between them with zero net work being done? Can this necessarily be done without exerting a force? Explain.
11. What is the relationship between voltage and energy? More precisely, what is the relationship between potential difference and electric potential energy?
12. Voltages are always measured between two points. Why?
13. How are units of volts and electron volts related? How do they differ?
10.6: Conductors and Applications of Electrostatics
14. Is the object in Figure \(\PageIndex{2}\) a conductor or an insulator? Justify your answer.
Figure \(\PageIndex{2}\)
15. If the electric field lines in the figure above were perpendicular to the object, would it necessarily be a conductor? Explain.
16. The discussion of the electric field between two parallel conducting plates, in this module states that edge effects are less important if the plates are close together. What does close mean? That is, is the actual plate separation crucial, or is the ratio of plate separation to plate area crucial?
17. Would the self-created electric field at the end of a pointed conductor, such as a lightning rod, remove positive or negative charge from the conductor? Would the same sign charge be removed from a neutral pointed conductor by the application of a similar externally created electric field? (The answers to both questions have implications for charge transfer utilizing points.)
18. Why is a golfer with a metal club over her shoulder vulnerable to lightning in an open fairway? Would she be any safer under a tree?
19. Can the belt of a Van de Graaff accelerator be a conductor? Explain.
20. Are you relatively safe from lightning inside an automobile? Give two reasons.
21. Discuss pros and cons of a lightning rod being grounded versus simply being attached to a building.
22. Using the symmetry of the arrangement, show that the net Coulomb force on the charge \(q\) at the center of the square below (Figure \(\PageIndex{3}\)) is zero if the charges on the four corners are exactly equal.
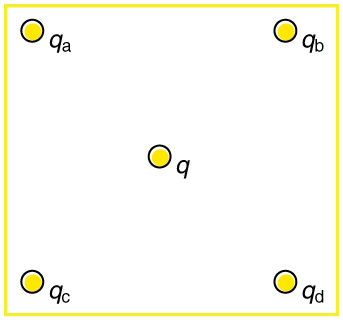
23. (a) Using the symmetry of the arrangement, show that the electric field at the center of the square in Figure \(\PageIndex{3}\) is zero if the charges on the four corners are exactly equal.
(b) Show that this is also true for any combination of charges in which \(q_{a}=q_{d}\) and \(q_{b}=q_{c}\)
24. (a) What is the direction of the total Coulomb force on \(q\) in Figure \(\PageIndex{3}\) if \(q\) is negative, \(q_{a}=q_{c}\) and both are negative, and \(q_{b}=q_{c}\) and both are positive?
(b) What is the direction of the electric field at the center of the square in this situation?
25. Considering Figure \(\PageIndex{3}\), suppose that \(q_{a}=q_{d}\) and \(q_{b}=q_{c}\). First show that \(q\) is in static equilibrium. (You may neglect the gravitational force.) Then discuss whether the equilibrium is stable or unstable, noting that this may depend on the signs of the charges and the direction of displacement of \(q\) from the center of the square.
26. If \(q_{a}=0\) in Figure \(\PageIndex{3}\), under what conditions will there be no net Coulomb force on \(q\)?
27. In regions of low humidity, one develops a special “grip” when opening car doors, or touching metal door knobs. This involves placing as much of the hand on the device as possible, not just the ends of one’s fingers. Discuss the induced charge and explain why this is done.
28. Tollbooth stations on roadways and bridges usually have a piece of wire stuck in the pavement before them that will touch a car as it approaches. Why is this done?
29. Suppose a woman carries an excess charge. To maintain her charged status can she be standing on ground wearing just any pair of shoes? How would you discharge her? What are the consequences if she simply walks away?
10.7: Current
30. Can a wire carry a current and still be neutral—that is, have a total charge of zero? Explain.
31. Car batteries are rated in ampere-hours (\(A \cdot h\)). To what physical quantity do ampere-hours correspond (voltage, charge, . . .), and what relationship do ampere-hours have to energy content?
32. Why are two conducting paths from a voltage source to an electrical device needed to operate the device?
33. In cars, one battery terminal is connected to the metal body. How does this allow a single wire to supply current to electrical devices rather than two wires?
34. Why isn’t a bird sitting on a high-voltage power line electrocuted? Contrast this with the situation in which a large bird hits two wires simultaneously with its wings.
10.8: Ohm’s Law- Resistance and Simple Circuits
35. The \(IR\) drop across a resistor means that there is a change in potential or voltage across the resistor. Is there any change in current as it passes through a resistor? Explain.
36. How is the \(IR\) drop in a resistor similar to the pressure drop in a fluid flowing through a pipe?
10.9: Electric Power and Energy
37. Why do incandescent lightbulbs grow dim late in their lives, particularly just before their filaments break?
38. The power dissipated in a resistor is given by \(P=V^{2} / R\), which means power decreases if resistance increases. Yet this power is also given by \(P=I^{2} R\), which means power increases if resistance increases. Explain why there is no contradiction here.
10.10: Resistors in Series and Parallel
39. A switch has a variable resistance that is nearly zero when closed and extremely large when open, and it is placed in series with the device it controls. Explain the effect the switch in Figure \(\PageIndex{4}\) has on current when open and when closed.
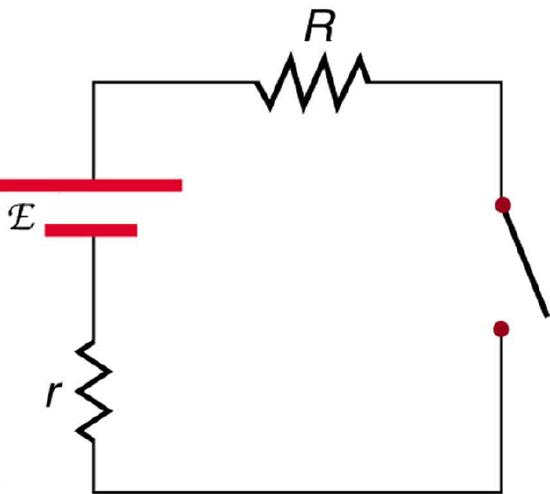
40. What is the voltage across the open switch in Figure \(\PageIndex{4}\)?
41. There is a voltage across an open switch, such as in Figure \(\PageIndex{4}\). Why, then, is the power dissipated by the open switch small?
42. Why is the power dissipated by a closed switch, such as in Figure \(\PageIndex{4}\), small?
43. A student in a physics lab mistakenly wired a light bulb, battery, and switch as shown in Figure \(\PageIndex{5}\). Explain why the bulb is on when the switch is open, and off when the switch is closed. (Do not try this—it is hard on the battery!)
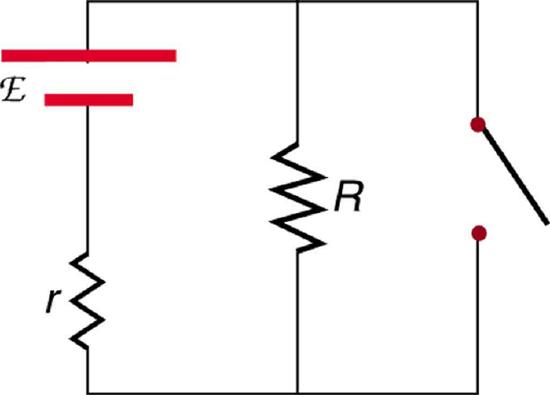
44. Knowing that the severity of a shock depends on the magnitude of the current through your body, would you prefer to be in series or parallel with a resistance, such as the heating element of a toaster, if shocked by it? Explain.
45. Would your headlights dim when you start your car’s engine if the wires in your automobile were superconductors? (Do not neglect the battery’s internal resistance.) Explain.
46. Some strings of holiday lights are wired in series to save wiring costs. An old version utilized bulbs that break the electrical connection, like an open switch, when they burn out. If one such bulb burns out, what happens to the others? If such a string operates on 120 V and has 40 identical bulbs, what is the normal operating voltage of each? Newer versions use bulbs that short circuit, like a closed switch, when they burn out. If one such bulb burns out, what happens to the others? If such a string operates on 120 V and has 39 remaining identical bulbs, what is then the operating voltage of each?
47. If two household lightbulbs rated 60 W and 100 W are connected in series to household power, which will be brighter? Explain.
48. Suppose you are doing a physics lab that asks you to put a resistor into a circuit, but all the resistors supplied have a larger resistance than the requested value. How would you connect the available resistances to attempt to get the smaller value asked for?
49. Before World War II, some radios got power through a “resistance cord” that had a significant resistance. Such a resistance cord reduces the voltage to a desired level for the radio’s tubes and the like, and it saves the expense of a transformer. Explain why resistance cords become warm and waste energy when the radio is on.
50. Some light bulbs have three power settings (not including zero), obtained from multiple filaments that are individually switched and wired in parallel. What is the minimum number of filaments needed for three power settings?
10.11: Electric Hazards and the Human Body
51. Using an ohmmeter, a student measures the resistance between various points on his body. He finds that the resistance between two points on the same finger is about the same as the resistance between two points on opposite hands—both are several hundred thousand ohms. Furthermore, the resistance decreases when more skin is brought into contact with the probes of the ohmmeter. Finally, there is a dramatic drop in resistance (to a few thousand ohms) when the skin is wet. Explain these observations and their implications regarding skin and internal resistance of the human body.
52. What are the two major hazards of electricity?
53. Why isn’t a short circuit a shock hazard?
54. What determines the severity of a shock? Can you say that a certain voltage is hazardous without further information?
55. An electrified needle is used to burn off warts, with the circuit being completed by having the patient sit on a large butt plate. Why is this plate large?
56. Some surgery is performed with high-voltage electricity passing from a metal scalpel through the tissue being cut. Considering the nature of electric fields at the surface of conductors, why would you expect most of the current to flow from the sharp edge of the scalpel? Do you think high- or low-frequency AC is used?
57. Some devices often used in bathrooms, such as hairdryers, often have safety messages saying “Do not use when the bathtub or basin is full of water.” Why is this so?
58. We are often advised to not flick electric switches with wet hands, dry your hand first. We are also advised to never throw water on an electric fire. Why is this so?
59. Before working on a power transmission line, linemen will touch the line with the back of the hand as a final check that the voltage is zero. Why the back of the hand?
60. Why is the resistance of wet skin so much smaller than dry, and why do blood and other bodily fluids have low resistances?
61. Could a person on intravenous infusion (an IV) be microshock sensitive?
62. In view of the small currents that cause shock hazards and the larger currents that circuit breakers and fuses interrupt, how do they play a role in preventing shock hazards?
Problems & Exercises
10.1: Static Electricity and Charge- Conservation of Charge
63. Common static electricity involves charges ranging from nanocoulombs to microcoulombs.
(a) How many electrons are needed to form a charge of –2.00 nC
(b) How many electrons must be removed from a neutral object to leave a net charge of \(0.500 \ \mu \mathrm{C}\)?
Solution
(a) 1.25×1010
(b) 3.13×1012
64. If 1.80×1020 electrons move through a pocket calculator during a full day’s operation, how many coulombs of charge moved through it?
65. To start a car engine, the car battery moves 3.75×1021 electrons through the starter motor. How many coulombs of charge were moved?
Solution
-600 C
66. A certain lightning bolt moves 40.0 C of charge. How many fundamental units of charge \(\left|q_{e}\right|\) is this?
10.2: Coulomb’s Law
67. What is the repulsive force between two pith balls that are 8.00 cm apart and have equal charges of – 30.0 nC?
68. (a) How strong is the attractive force between a glass rod with a \(0.700 \ \mu \mathrm{C}\) charge and a silk cloth with a \(-0.600 \ \mu \mathrm{C}\) charge, which are 12.0 cm apart, using the approximation that they act like point charges?
(b) Discuss how the answer to this problem might be affected if the charges are distributed over some area and do not act like point charges.
Solution
(a) 0.263 N
(b) If the charges are distributed over some area, there will be a concentration of charge along the side closest to the oppositely charged object. This effect will increase the net force.
69. Two point charges exert a 5.00 N force on each other. What will the force become if the distance between them is increased by a factor of three?
70. Two point charges are brought closer together, increasing the force between them by a factor of 25. By what factor was their separation decreased?
Solution
The separation decreased by a factor of 5.
71. How far apart must two point charges of 75.0 nC (typical of static electricity) be to have a force of 1.00 N between them?
72. If two equal charges each of 1 C each are separated in air by a distance of 1 km, what is the magnitude of the force acting between them? You will see that even at a distance as large as 1 km, the repulsive force is substantial because 1 C is a very significant amount of charge.
73. Bare free charges do not remain stationary when close together. To illustrate this, calculate the acceleration of two isolated protons separated by 2.00 nm (a typical distance between gas atoms).
Solution
\(\begin{aligned}
F &=k \frac{\left|q_{1} q_{2}\right|}{r^{2}}=m a \Rightarrow a=\frac{k q^{2}}{m r^{2}} \\
&=\frac{\left(9.00 \times 10^{9} \mathrm{~N} \cdot \mathrm{m}^{2} / \mathrm{C}^{2}\right)\left(1.60 \times 10^{-19} \mathrm{~m}\right)^{2}}{\left(1.67 \times 10^{-27} \mathrm{~kg}\right)\left(2.00 \times 10^{-9} \mathrm{~m}\right)^{2}} \\
&=3.45 \times 10^{16} \mathrm{~m} / \mathrm{s}^{2}
\end{aligned}\)
74. (a) By what factor must you change the distance between two point charges to change the force between them by a factor of 10?
(b) Explain how the distance can either increase or decrease by this factor and still cause a factor of 10 change in the force.
Solution
(a) 3.2
(b) If the distance increases by 3.2, then the force will decrease by a factor of 10 ; if the distance decreases by 3.2, then the force will increase by a factor of 10. Either way, the force changes by a factor of 10.
75. Suppose you have a total charge \(q_{\text {tot }}\) that you can split in any manner. Once split, the separation distance is fixed. How do you split the charge to achieve the greatest force?
76. (a) Common transparent tape becomes charged when pulled from a dispenser. If one piece is placed above another, the repulsive force can be great enough to support the top piece’s weight. Assuming equal point charges (only an approximation), calculate the magnitude of the charge if electrostatic force is great enough to support the weight of a 10.0 mg piece of tape held 1.00 cm above another.
(b) Discuss whether the magnitude of this charge is consistent with what is typical of static electricity.
Solution
(a) 1.04×10−9 C
(b) This charge is approximately 1 nC, which is consistent with the magnitude of charge typical for static electricity
77. (a) Find the ratio of the electrostatic to gravitational force between two electrons.
(b) What is this ratio for two protons?
(c) Why is the ratio different for electrons and protons?
78. At what distance is the electrostatic force between two protons equal to the weight of one proton?
79. A certain five cent coin contains 5.00 g of nickel. What fraction of the nickel atoms’ electrons, removed and placed 1.00 m above it, would support the weight of this coin? The atomic mass of nickel is 58.7, and each nickel atom contains 28 electrons and 28 protons.
Solution
1.02×10−11
80. (a) Two point charges totaling \(8.00 \ \mu \mathrm{C}\) exert a repulsive force of 0.150 N on one another when separated by 0.500 m. What is the charge on each?
(b) What is the charge on each if the force is attractive?
10.3: Electric Field- Concept of a Field Revisited
81. What is the magnitude and direction of an electric field that exerts a 2.00×10−5 N upward force on a \(-1.75 \ \mu \mathrm{C}\) charge?
82. What is the magnitude and direction of the force exerted on a \(3.50 \ \mu \mathrm{C}\) charge by a 250 N/C electric field that points due east?
Solution
8.75×10−4 N
83. Calculate the magnitude of the electric field 2.00 m from a point charge of 5.00 mC (such as found on the terminal of a Van de Graaff).
84. (a) What magnitude point charge creates a 10,000 N/C electric field at a distance of 0.250 m?
(b) How large is the field at 10.0 m?
Solution
(a) 6.94×10−8 C
(b) 6.25 N/C
85. Calculate the initial (from rest) acceleration of a proton in a 5.00×106 N/C electric field (such as created by a research Van de Graaff). Explicitly show how you follow the steps in the Problem-Solving Strategy for electrostatics.
86. (a) Find the direction and magnitude of an electric field that exerts a 4.80×10−17 N westward force on an electron.
(b) What magnitude and direction force does this field exert on a proton?
Solution
(a) 300 N/C (east)
(b) 4.80×10−17 N (east)
10.4: Electric Field Lines
87. (a) Sketch the electric field lines near a point charge \(+q\). (b) Do the same for a point charge \(-3.00 q\).
88. Sketch the electric field lines a long distance from the charge distributions shown in Figure 10.4.4 (a) and (b)
89. Figure \(\PageIndex{6}\) shows the electric field lines near two charges \(q_{1}\) and \(q_{2}\). What is the ratio of their magnitudes? (b) Sketch the electric field lines a long distance from the charges shown in the figure.
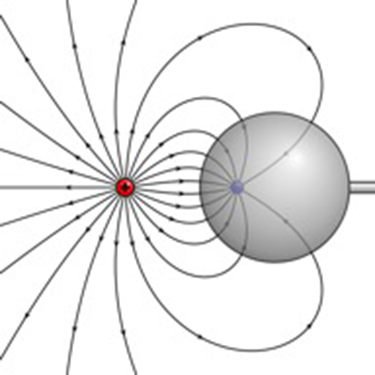
90. Sketch the electric field lines in the vicinity of two opposite charges, where the negative charge is three times greater in magnitude than the positive. (See Figure \(\PageIndex{6}\) for a similar situation).
10.5: Electric Potential and Potential Energy
91. Find the ratio of speeds of an electron and a negative hydrogen ion (one having an extra electron) accelerated through the same voltage, assuming non-relativistic final speeds. Take the mass of the hydrogen ion to be \(1.67 \times 10^{-27} \mathrm{~kg}\).
Solution
42.8
92. An evacuated tube uses an accelerating voltage of 40 kV to accelerate electrons to hit a copper plate and produce X-rays. Non-relativistically, what would be the maximum speed of these electrons?
93. A bare helium nucleus has two positive charges and a mass of \(6.64 \times 10^{-27} \mathrm{~kg}\)
(a) Calculate its kinetic energy in joules at 2.00% of the speed of light.
(b) What is this in electron volts?
(c) What voltage would be needed to obtain this energy?
Integrated Concepts
94. Singly charged gas ions are accelerated from rest through a voltage of 13.0 V. At what temperature will the average kinetic energy of gas molecules be the same as that given these ions?
Solution
\(1.00 \times 10^{5} \mathrm{~K}\)
Integrated Concepts
95. The temperature near the center of the Sun is thought to be 15 million degrees Celsius \(\left(1.5 \times 10^{7}{ }^{\circ} \mathrm{C}\right)\). Through what voltage must a singly charged ion be accelerated to have the same energy as the average kinetic energy of ions at this temperature?
Integrated Concepts
96. (a) What is the average power output of a heart defibrillator that dissipates 400 J of energy in 10.0 ms?
(b) Considering the high-power output, why doesn’t the defibrillator produce serious burns?
Solution
(a) \(4 \times 10^{4} \mathrm{~W}\)
(b) A defibrillator does not cause serious burns because the skin conducts electricity well at high voltages, like those used in defibrillators. The gel used aids in the transfer of energy to the body, and the skin doesn’t absorb the energy, but rather lets it pass through to the heart.
Integrated Concepts
97. A lightning bolt strikes a tree, moving 20.0 C of charge through a potential difference of \(1.00 \times 10^{2} \ \mathrm{MV}\).
(a) What energy was dissipated?
(b) What mass of water could be raised from \(15^{\circ} \mathrm{C}\) to the boiling point and then boiled by this energy?
(c) Discuss the damage that could be caused to the tree by the expansion of the boiling steam.
Integrated Concepts
98. A 12.0 V battery-operated bottle warmer heats 50.0 g of glass, \(2.50 \times 10^{2} \mathrm{~g}\) of baby formula, and \(2.00 \times 10^{2} \mathrm{~g}\) of aluminum from \(20.0^{\circ} \mathrm{C}\) to \(90.0^{\circ} \mathrm{C}\).
(a) How much charge is moved by the battery?
(b) How many electrons per second flow if it takes 5.00 min to warm the formula? (Hint: Assume that the specific heat of baby formula is about the same as the specific heat of water.)
Solution
(a) \(7.40 \times 10^{3} \mathrm{C}\)
(b) \(1.54 \times 10^{20} \text { electrons per second }\)
Integrated Concepts
99. A battery-operated car utilizes a 12.0 V system. Find the charge the batteries must be able to move in order to accelerate the 750 kg car from rest to 25.0 m/s, make it climb a \(2.00 \times 10^{2} \mathrm{~m}\) high hill, and then cause it to travel at a constant 25.0 m/s by exerting a \(5.00 \times 10^{2} \mathrm{~N}\) force for an hour.
Solution
\(3.89 \times 10^{6} \mathrm{C}\)
Integrated Concepts
100. Fusion probability is greatly enhanced when appropriate nuclei are brought close together, but mutual Coulomb repulsion must be overcome. This can be done using the kinetic energy of high-temperature gas ions or by accelerating the nuclei toward one another.
(a) Calculate the potential energy of two singly charged nuclei separated by \(1.00 \times 10^{-12} \mathrm{~m}\) by finding the voltage of one at that distance and multiplying by the charge of the other.
(b) At what temperature will atoms of a gas have an average kinetic energy equal to this needed electrical potential energy?
10.7: Current
101. What is the current in milliamperes produced by the solar cells of a pocket calculator through which 4.00 C of charge passes in 4.00 h?
Solution
0.278 mA
102. A total of 600 C of charge passes through a flashlight in 0.500 h. What is the average current?
103. What is the current when a typical static charge of \(0.250 \ \mu \mathrm{C}\) moves from your finger to a metal doorknob in \(1.00 \ \mu \mathrm{s} ?\)?
Solution
0.250 A
104. Find the current when 2.00 nC jumps between your comb and hair over a \(0.500-\mu \mathrm{s}\) time interval.
105. A large lightning bolt had a 20,000-A current and moved 30.0 C of charge. What was its duration?
Solution
1.50ms
106. The 200-A current through a spark plug moves 0.300 mC of charge. How long does the spark last?
107. (a) A defibrillator passes 12.0 A of current through the torso of a person for 0.0100 s. How much charge moves?
(b) How many electrons pass through the wires connected to the patient? (See figure two problems earlier.)
Solution
(a) 0.120 C
(b) \(7.50 \times 10^{17} \text { electrons }\)
108. A clock battery wears out after moving 10,000 C of charge through the clock at a rate of 0.500 mA.
(a) How long did the clock run?
(b) How many electrons per second flowed?
109. The batteries of a submerged non-nuclear submarine supply 1000 A at full speed ahead. How long does it take to move Avogadro’s number (\(6.02 \times 10^{23}\)) of electrons at this rate?
Solution
96.3 s
110. Electron guns are used in X-ray tubes. The electrons are accelerated through a relatively large voltage and directed onto a metal target, producing X-rays.
(a) How many electrons per second strike the target if the current is 0.500 mA?
(b) What charge strikes the target in 0.750 s?
112. A large cyclotron directs a beam of \(\mathrm{He}^{++}\) nuclei onto a target with a beam current of 0.250 mA.
(a) How many \(\mathrm{He}^{++}\) nuclei per second is this?
(b) How long does it take for 1.00 C to strike the target?
(c) How long before 1.00 mol of \(\mathrm{He}^{++}\) nuclei strike the target?
Solution
(a) \(7.81 \times 10^{14} \ \mathrm{He}^{++} \text {nuclei/s }\)
(b) \(4.00 \times 10^{3} \mathrm{~s}\)
(c) \(7.71 \times 10^{8} \mathrm{~s}\)
10.8: Ohm’s Law- Resistance and Simple Circuits
113. What current flows through the bulb of a 3.00-V flashlight when its hot resistance is \(3.60 \ \Omega\)?
Solution
0.833 A
114. Calculate the effective resistance of a pocket calculator that has a 1.35-V battery and through which 0.200 mA flows.
115. What is the effective resistance of a car’s starter motor when 150 A flows through it as the car battery applies 11.0 V to the motor?
Solution
\[7.33 \times 10^{-2} \ \Omega \nonumber\]
116. How many volts are supplied to operate an indicator light on a DVD player that has a resistance of \(140 \ \Omega\), given that 25.0 mA passes through it?
117. (a) Find the voltage drop in an extension cord having a \(0.0600-\Omega\) resistance and through which 5.00 A is flowing.
(b) A cheaper cord utilizes thinner wire and has a resistance of \(0.300 \ \Omega\). What is the voltage drop in it when 5.00 A flows?
(c) Why is the voltage to whatever appliance is being used reduced by this amount? What is the effect on the appliance?
Solution
(a) 0.300 V
(b) 1.50 V
(c) The voltage supplied to whatever appliance is being used is reduced because the total voltage drop from the wall to the final output of the appliance is fixed. Thus, if the voltage drop across the extension cord is large, the voltage drop across the appliance is significantly decreased, so the power output by the appliance can be significantly decreased, reducing the ability of the appliance to work properly.
118. A power transmission line is hung from metal towers with glass insulators having a resistance of \(1.00 \times 10^{9} \ \Omega\) What current flows through the insulator if the voltage is 200 kV? (Some high-voltage lines are DC.)
10.9: Electric Power and Energy
119. What is the power of a \(1.00 \ \times 10^{2} \mathrm{MV}\) lightning bolt having a current of \(2.00 \times 10^{4} \mathrm{~A}\)?
Solution
\(2.00 \times 10^{12} \mathrm{~W}\)
120. What power is supplied to the starter motor of a large truck that draws 250 A of current from a 24.0-V battery hookup?
121. A charge of 4.00 C of charge passes through a pocket calculator’s solar cells in 4.00 h. What is the power output, given the calculator’s voltage output is 3.00 V? (See Figure \(\PageIndex{7}\).)
122. How many watts does a flashlight that has \(6.00 \times 10^{2} \ \mathrm{C}\) pass through it in 0.500 h use if its voltage is 3.00 V?
123. Find the power dissipated in each of these extension cords:
(a) an extension cord having a \(0.0600-\Omega\) resistance and through which 5.00 A is flowing;
(b) a cheaper cord utilizing thinner wire and with a resistance of \(0.300 \ \Omega \).
Solution
(a) 1.50 W
(b) 7.50 W
124. Verify that the units of a volt-ampere are watts, as implied by the equation \(P=I V\).
125. Show that the units \(1 \mathrm{~V}^{2} / \Omega=1 \mathrm{~W}\), as implied by the equation \(P=V^{2} / R\).
Solution
\(\frac{\mathrm{V}^{2}}{\Omega}=\frac{\mathrm{V}^{2}}{\mathrm{~V} / \mathrm{A}}=\mathrm{AV}=\left(\frac{\mathrm{C}}{\mathrm{s}}\right)\left(\frac{\mathrm{J}}{\mathrm{C}}\right)=\frac{\mathrm{J}}{\mathrm{s}}=1 \mathrm{~W}\)
126. Show that the units \(1 \mathrm{~A}^{2} \cdot \Omega=1 \mathrm{~W}\), as implied by the equation \(P=I^{2} R\).
127. Verify the energy unit equivalence that \(1 \mathrm{~kW} \cdot \mathrm{h}=3.60 \times 10^{6} \mathrm{~J}\).
Solution
\(1 \mathrm{~kW} \cdot \mathrm{h}=\left(\frac{1 \times 10^{3} \mathrm{~J}}{1 \mathrm{~s}}\right)(1 \mathrm{~h})\left(\frac{3600 \mathrm{~s}}{1 \mathrm{~h}}\right)=3.60 \times 10^{6} \mathrm{~J}\)
128. Electrons in an X-ray tube are accelerated through \(1.00 \times 10^{2} \ \mathrm{kV}\) and directed toward a target to produce X-rays. Calculate the power of the electron beam in this tube if it has a current of 15.0 mA.
129. An electric water heater consumes 5.00 kW for 2.00 h per day. What is the cost of running it for one year if electricity costs \(12.0 \text { cents } / \mathrm{kW} \cdot \mathrm{h}\)? See Figure \(\PageIndex{8}\).
Solution
$438/y
130. With a 1200-W toaster, how much electrical energy is needed to make a slice of toast (cooking time = 1 minute)? At \(9.0 \text { cents } / \mathrm{kW} \cdot \mathrm{h}\), how much does this cost?
131. Some makes of older cars have 6.00-V electrical systems.
(a) What is the hot resistance of a 30.0-W headlight in such a car?
(b) What current flows through it?
132. Alkaline batteries have the advantage of putting out constant voltage until very nearly the end of their life. How long will an alkaline battery rated at \(1.00 \mathrm{~A} \cdot \mathrm{h}\) and 1.58 V keep a 1.00-W flashlight bulb burning?
Solution
1.58 h
133. A cauterizer, used to stop bleeding in surgery, puts out 2.00 mA at 15.0 kV.
(a) What is its power output?
(b) What is the resistance of the path?
134. The average television is said to be on 6 hours per day. Estimate the yearly cost of electricity to operate 100 million TVs, assuming their power consumption averages 150 W and the cost of electricity averages \(12.0 \text { cents} / \mathrm{kW} \cdot \mathrm{h}\).
Solution
$3.94 billion/year
10.10: Resistors in Series and Parallel
Note: Data taken from figures can be assumed to be accurate to three significant digits.
135. (a) What is the resistance of ten \(275-\Omega\) resistors connected in series?
(b) In parallel?
Solution
(a) \(2.75 ~\mathrm{k} \Omega\)
(b) \(27.5 ~\Omega\)
136. (a) What is the resistance of a \(1.00 \times 10^{2}-\Omega\), a \(2.50-\mathrm{k} ~\Omega\), and a \(4.00-\mathrm{k} ~\Omega\) resistor connected in series?
(b) In parallel?
137. What are the largest and smallest resistances you can obtain by connecting a \(36.0-\Omega\), a \(50.0-\Omega\), and a \(700-\Omega\) resistor together?
Solution
(a) \(786 ~\Omega\)
(b) \(20.3 ~\Omega\)
138. An 1800-W toaster, a 1400-W electric frying pan, and a 75-W lamp are plugged into the same outlet in a 15-A, 120-V circuit. (The three devices are in parallel when plugged into the same socket.).
(a) What current is drawn by each device?
(b) Will this combination blow the 15-A fuse?
139. Your car’s 30.0-W headlight and 2.40-kW starter are ordinarily connected in parallel in a 12.0-V system. What power would one headlight and the starter consume if connected in series to a 12.0-V battery? (Neglect any other resistance in the circuit and any change in resistance in the two devices.)
Solution
\(29.6 \mathrm{~W}\)
140. (a) Given a 48.0-V battery and \(24.0-\Omega\) and \(96.0-\Omega\) resistors, find the current and power for each when connected in series.
(b) Repeat when the resistances are in parallel.
141. Referring to the example combining series and parallel circuits and Figure 10.10.5, calculate \(I_{3}\) in the following two different ways: (a) from the known values of \(I\) and \(I_{2}\); (b) using Ohm’s law for \(R_{3}\). In both parts explicitly show how you follow the steps in the Problem-Solving Strategies for Series and Parallel Resistors.
Solution
(a) 0.74 A
(b) 0.742 A
142. Referring to Figure: 10.10.5(a) Calculate \(P_{3}\) and note how it compares with \(P_{3}\) found in the first two example problems in this module. (b) Find the total power supplied by the source and compare it with the sum of the powers dissipated by the resistors.
143. Refer to Figure 10.10.6 and the discussion of lights dimming when a heavy appliance comes on. (a) Given the voltage source is 120 V, the wire resistance is \(0.400 ~\Omega\), and the bulb is nominally 75.0 W, what power will the bulb dissipate if a total of 15.0 A passes through the wires when the motor comes on? Assume negligible change in bulb resistance. (b) What power is consumed by the motor?
Solution
(a) 60.8 W
(b) 3.18 kW
144. A 240-kV power transmission line carrying \(5.00 \times 10^{2} \mathrm{~A}\) is hung from grounded metal towers by ceramic insulators, each having a \(1.00 \times 10^{9}-\Omega\) resistance. Figure \(\PageIndex{9}\). (a) What is the resistance to ground of 100 of these insulators? (b) Calculate the power dissipated by 100 of them. (c) What fraction of the power carried by the line is this? Explicitly show how you follow the steps in the Problem-Solving Strategies for Series and Parallel Resistors.
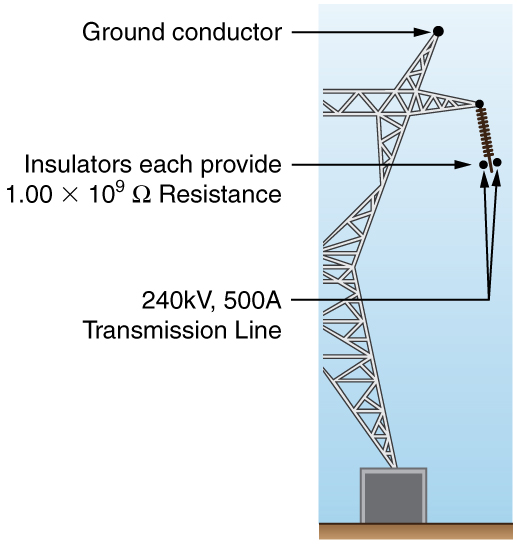
145. Show that if two resistors \(R_{1}\) and \(R_{2}\) are combined and one is much greater than the other \(\left(R_{1}>>R_{2}\right)\):
(a) Their series resistance is very nearly equal to the greater resistance \(R_{1}\).
(b) Their parallel resistance is very nearly equal to smaller resistance \(R_{2}\).
Solution
(a) \(\begin{gathered}
R_{\mathrm{s}}=R_{1}+R_{2} \\
\Rightarrow R_{\mathrm{s}} \approx R_{1}\left(R_{1}>>R_{2}\right)
\end{gathered}\)
(b) \(\frac{1}{R_{\mathrm{p}}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}=\frac{R_{1}+R_{2}}{R_{1} R_{2}}, \)
so that
\(R_{\mathrm{p}}=\frac{R_{1} R_{2}}{R_{1}+R_{2}} \approx \frac{R_{1} R_{2}}{R_{1}}=R_{2}\left(R_{1}>>R_{2}\right)\).
Unreasonable Results
146. Two resistors, one having a resistance of \(145 ~\Omega\), are connected in parallel to produce a total resistance of \(150 ~\Omega\).
(a) What is the value of the second resistance?
(b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Unreasonable Results
147. Two resistors, one having a resistance of \(900 ~\mathrm{k} \Omega\), are connected in series to produce a total resistance of \(0.500 \mathrm{M} ~\Omega\).
(a) What is the value of the second resistance?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
Solution
(a) \(-400 ~\mathrm{k} \Omega\)
(b) Resistance cannot be negative.
(c) Series resistance is said to be less than one of the resistors, but it must be greater than any of the resistors.
10.11: Electric Hazards and the Human Body
148. (a) How much power is dissipated in a short circuit of 240-V AC through a resistance of \(0.250 ~\Omega\)?
(b) What current flows?
Solution
(a) 230 kW
(b) 960 A
149. What voltage is involved in a 1.44-kW short circuit through a \(0.100-\Omega\) resistance?
150. Find the current through a person and identify the likely effect on her if she touches a 120-V AC source:
(a) if she is standing on a rubber mat and offers a total resistance of \(300 ~\mathrm{k} \Omega\);
(b) if she is standing barefoot on wet grass and has a resistance of only \(4000 ~\mathrm{k} \Omega\).
Solution
(a) 0.400 mA, no effect
(b) 26.7 mA, muscular contraction for duration of the shock (can't let go)
151. While taking a bath, a person touches the metal case of a radio. The path through the person to the drainpipe and ground has a resistance of \(4000 ~\Omega\). What is the smallest voltage on the case of the radio that could cause ventricular fibrillation?
152. Foolishly trying to fish a burning piece of bread from a toaster with a metal butter knife, a man comes into contact with 120-V AC. He does not even feel it since, luckily, he is wearing rubber-soled shoes. What is the minimum resistance of the path the current follows through the person?
Solution
\(1.20 \times 10^{5} ~\Omega\)
153. (a) During surgery, a current as small as \(20.0 \mu \mathrm{A}\) applied directly to the heart may cause ventricular fibrillation. If the resistance of the exposed heart is \(300 ~\Omega\), what is the smallest voltage that poses this danger?
(b) Does your answer imply that special electrical safety precautions are needed?
154. (a) What is the resistance of a 220-V AC short circuit that generates a peak power of 96.8 kW?
(b) What would the average power be if the voltage was 120 V AC?
Solution
(a) \(1.00 ~\Omega\)
(b) 14.4 kW
155. A heart defibrillator passes 10.0 A through a patient’s torso for 5.00 ms in an attempt to restore normal beating.
(a) How much charge passed?
(b) What voltage was applied if 500 J of energy was dissipated?
(c) What was the path’s resistance?
(d) Find the temperature increase caused in the 8.00 kg of affected tissue.
Integrated Concepts
156. A short circuit in a 120-V appliance cord has a \(0.500-\Omega\) resistance. Calculate the temperature rise of the 2.00 g of surrounding materials, assuming their specific heat capacity is \(0.200 \mathrm{cal} / \mathrm{g} \cdot{ }^{\circ} \mathrm{C}\) and that it takes 0.0500 s for a circuit breaker to interrupt the current. Is this likely to be damaging?
Solution
Temperature increases \(860^{\circ} ~\mathrm{C}\). It is very likely to be damaging.
Construct Your Own Problem
157. Consider a person working in an environment where electric currents might pass through her body. Construct a problem in which you calculate the resistance of insulation needed to protect the person from harm. Among the things to be considered are the voltage to which the person might be exposed, likely body resistance (dry, wet, …), and acceptable currents (safe but sensed, safe and unfelt, …).