1.4: Thermal Expansion
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Answer qualitative questions about the effects of thermal expansion
- Solve problems involving thermal expansion, including those involving thermal stress
The expansion of alcohol in a thermometer is one of many commonly encountered examples of thermal expansion, which is the change in size or volume of a given system as its temperature changes. The most visible example is the expansion of hot air. When air is heated, it expands and becomes less dense than the surrounding air, which then exerts an (upward) force on the hot air and makes steam and smoke rise, hot air balloons float, and so forth. The same behavior happens in all liquids and gases, driving natural heat transfer upward in homes, oceans, and weather systems, as we will discuss in an upcoming section. Solids also undergo thermal expansion. Railroad tracks and bridges, for example, have expansion joints to allow them to freely expand and contract with temperature changes, as shown in Figure 1.4.1.

What is the underlying cause of thermal expansion? As previously mentioned, an increase in temperature means an increase in the kinetic energy of individual atoms. In a solid, unlike in a gas, the molecules are held in place by forces from neighboring molecules; as we saw in Oscillations, the forces can be modeled as in harmonic springs described by the Lennard-Jones potential. Energy in Simple Harmonic Motion shows that such potentials are asymmetrical in that the potential energy increases more steeply when the molecules get closer to each other than when they get farther away. Thus, at a given kinetic energy, the distance moved is greater when neighbors move away from each other than when they move toward each other. The result is that increased kinetic energy (increased temperature) increases the average distance between molecules—the substance expands.
For most substances under ordinary conditions, it is an excellent approximation that there is no preferred direction (that is, the solid is “isotropic”), and an increase in temperature increases the solid’s size by a certain fraction in each dimension. Therefore, if the solid is free to expand or contract, its proportions stay the same; only its overall size changes.
According to experiments, the dependence of thermal expansion on temperature, substance, and original length is summarized in the equation
dLdT=αL
where L is the original length dLdT is the change in length with respect to temperature, and α is the coefficient of linear expansion, a material property that varies slightly with temperature. As α is nearly constant and also very small, for practical purposes, we use the linear approximation:
ΔL≈αLΔT.
Table 1.4.1 lists representative values of the coefficient of linear expansion. As noted earlier, ΔT is the same whether it is expressed in units of degrees Celsius or kelvins; thus, α may have units of 1/oC or 1/K with the same value in either case. Approximating α as a constant is quite accurate for small changes in temperature and sufficient for most practical purposes, even for large changes in temperature. We examine this approximation more closely in the next example.
| Material | Coefficient of Linear Expansion α(1/oC) | Coefficient of Volume Expansion β(1/oC) |
|---|---|---|
| Solids | ||
| Aluminum | 25×10−6 | 75×10−6 |
| Brass | 19×10−6 | 56×10−6 |
| Copper | 17×10−6 | 51×10−6 |
| Gold | 14×10−6 | 42×10−6 |
| Iron or steel | 12×10−6 | 35×10−6 |
| Invar (nickel-iron alloy) | 0.9×10−6 | 2.7×10−6 |
| Lead | 29×10−6 | 87×10−6 |
| Silver | 18×10−6 | 54×10−6 |
| Glass (ordinary) | 9×10−6 | 27×10−6 |
| Glass (Pyrex®) | 3×10−6 | 9×10−6 |
| Quartz | 0.4×10−6 | 1×10−6 |
| Concrete, brick | −12×10−6 | −36×10−6 |
| Marble (average) | 2.5×10−6 | 7.5×10−6 |
| Liquids | ||
| Ether | 1650×10−6 | |
| Ethyl alcohol | 1100×10−6 | |
| Gasoline | 950×10−6 | |
| Glycerin | 500×10−6 | |
| Mercury | 180×10−6 | |
| Water | 210×10−6 | |
| Gases | ||
| Air and most other gases at atmospheric pressure | 3400×10−6 | |
Thermal expansion is exploited in the bimetallic strip (Figure 1.4.2). This device can be used as a thermometer if the curving strip is attached to a pointer on a scale. It can also be used to automatically close or open a switch at a certain temperature, as in older or analog thermostats.

The main span of San Francisco’s Golden Gate Bridge is 1275 m long at its coldest. The bridge is exposed to temperatures ranging from −15oC to 40oC. What is its change in length between these temperatures? Assume that the bridge is made entirely of steel.
Strategy
Use the equation for linear thermal expansion ΔL=αLΔT to calculate the change in length, ΔL. Use the coefficient of linear expansion α for steel from Table 1.4.1, and note that the change in temperature ΔT is 55oC.
Solution
Substitute all of the known values into the equation to solve for ΔL:
ΔL=αLΔT=(12×10−6oC)(1275m)(55oC)=0.84m.
Significance
Although not large compared with the length of the bridge, this change in length is observable. It is generally spread over many expansion joints so that the expansion at each joint is small.
Thermal Expansion in Two and Three Dimensions
Unconstrained objects expand in all dimensions, as illustrated in Figure 1.4.3. That is, their areas and volumes, as well as their lengths, increase with temperature. Because the proportions stay the same, holes and container volumes also get larger with temperature. If you cut a hole in a metal plate, the remaining material will expand exactly as it would if the piece you removed were still in place. The piece would get bigger, so the hole must get bigger too.
For small temperature changes, the change in area ΔA is given by
ΔA=2αAΔT
where ΔA is the range area A, ΔT is the change in temperature, and α is the coefficient of linear expansion, which varies slightly with temperature.
The relationship between volume and temperature dVdT is given by dVdT=βVΔT, where β is the coefficient of volume expansion. As you can show in Exercise, β=3α. This equation is usually written as
ΔV=βVΔT.
Note that the values of β in Table 1.4.1 are equal to 3α except for rounding.
Volume expansion is defined for liquids, but linear and area expansion are not, as a liquid’s changes in linear dimensions and area depend on the shape of its container. Thus, Table 1.4.1 shows liquids’ values of β but not α.
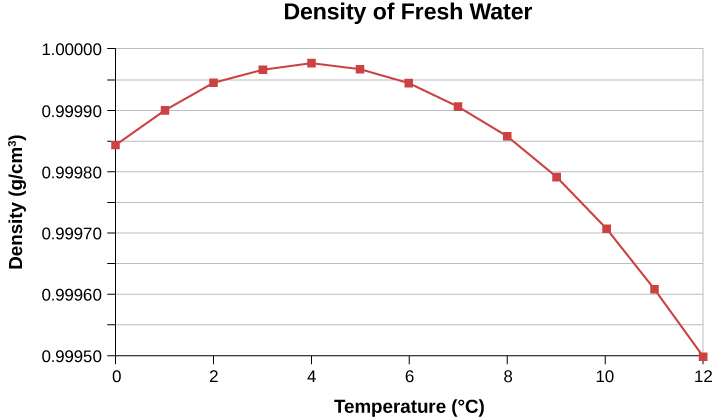
In general, objects expand with increasing temperature. Water is the most important exception to this rule. Water does expand with increasing temperature (its density decreases) at temperatures greater than 4oC(40oF). However, it is densest at +4oC and expands with decreasing temperature between +4oC and 0oC (40oFto32oF), as shown in Figure 1.4.4. A striking effect of this phenomenon is the freezing of water in a pond. When water near the surface cools down to 4oC, it is denser than the remaining water and thus sinks to the bottom. This “turnover” leaves a layer of warmer water near the surface, which is then cooled. However, if the temperature in the surface layer drops below 4oC, that water is less dense than the water below, and thus stays near the top. As a result, the pond surface can freeze over. The layer of ice insulates the liquid water below it from low air temperatures. Fish and other aquatic life can survive in 4oC water beneath ice, due to this unusual characteristic of water.
Suppose your 60.0-L (15.9-gal) steel gasoline tank is full of gas that is cool because it has just been pumped from an underground reservoir. Now, both the tank and the gasoline have a temperature of 15.0oC. How much gasoline has spilled by the time they warm to 35.0oC?
Strategy
The tank and gasoline increase in volume, but the gasoline increases more, so the amount spilled is the difference in their volume changes. We can use the equation for volume expansion to calculate the change in volume of the gasoline and of the tank. (The gasoline tank can be treated as solid steel.)
Solution
- Use the equation for volume expansion to calculate the increase in volume of the steel tank: ΔVs=βsVsΔT.
- The increase in volume of the gasoline is given by this equation: ΔVgas=βgasVgasΔT.
- Find the difference in volume to determine the amount spilled as Vspill=ΔVgas−ΔVs.
Alternatively, we can combine these three equations into a single equation. (Note that the original volumes are equal.)
Vspill=(βgas−βs)VΔT=[(950−35)×10−6/oC](60.0L)(20.0oC)=1.10L.
Significance
This amount is significant, particularly for a 60.0-L tank. The effect is so striking because the gasoline and steel expand quickly. The rate of change in thermal properties is discussed later in this chapter.
If you try to cap the tank tightly to prevent overflow, you will find that it leaks anyway, either around the cap or by bursting the tank. Tightly constricting the expanding gas is equivalent to compressing it, and both liquids and solids resist compression with extremely large forces. To avoid rupturing rigid containers, these containers have air gaps, which allow them to expand and contract without stressing them.
Does a given reading on a gasoline gauge indicate more gasoline in cold weather or in hot weather, or does the temperature not matter?
- Answer
-
The actual amount (mass) of gasoline left in the tank when the gauge hits “empty” is less in the summer than in the winter. The gasoline has the same volume as it does in the winter when the “add fuel” light goes on, but because the gasoline has expanded, there is less mass.
Thermal Stress
If you change the temperature of an object while preventing it from expanding or contracting, the object is subjected to stress that is compressive if the object would expand in the absence of constraint and tensile if it would contract. This stress resulting from temperature changes is known as thermal stress. It can be quite large and can cause damage.
To avoid this stress, engineers may design components so they can expand and contract freely. For instance, in highways, gaps are deliberately left between blocks to prevent thermal stress from developing. When no gaps can be left, engineers must consider thermal stress in their designs. Thus, the reinforcing rods in concrete are made of steel because steel’s coefficient of linear expansion is nearly equal to that of concrete.
To calculate the thermal stress in a rod whose ends are both fixed rigidly, we can think of the stress as developing in two steps. First, let the ends be free to expand (or contract) and find the expansion (or contraction). Second, find the stress necessary to compress (or extend) the rod to its original length by the methods you studied in Static Equilibrium and Elasticity on static equilibrium and elasticity. In other words, the ΔL of the thermal expansion equals the ΔL of the elastic distortion (except that the signs are opposite).
Concrete blocks are laid out next to each other on a highway without any space between them, so they cannot expand. The construction crew did the work on a winter day when the temperature was 5oC. Find the stress in the blocks on a hot summer day when the temperature is 38oC. The compressive Young’s modulus of concrete is Y=20×109N/m2.
Strategy
According to the chapter on static equilibrium and elasticity, the stress F/A is given by
FA=YΔLL0,
where Y is the Young’s modulus of the material—concrete, in this case. In thermal expansion, ΔL=αL0δT. We combine these two equations by noting that the two ΔL's are equal, as stated above. Because we are not given L0 or A, we can obtain a numerical answer only if they both cancel out.
Solution
We substitute the thermal-expansion equation into the elasticity equation to get
FA=YαL0ΔTL0=YαΔT,
and as we hoped, L0 has canceled and A appears only in F/A, the notation for the quantity we are calculating.
Now we need only insert the numbers:
FA=(20×106N/m2)(12×10−6/oC)(38oC−5oC)=7.9×106N/m2.
Significance The ultimate compressive strength of concrete is 20×106N/m2, so the blocks are unlikely to break. However, the ultimate shear strength of concrete is only 2×106N/m2, so some might chip off.
Two objects A and B have the same dimensions and are constrained identically. A is made of a material with a higher thermal expansion coefficient than B. If the objects are heated identically, will A feel a greater stress than B?
- Answer
-
Not necessarily, as the thermal stress is also proportional to Young’s modulus.


