23.2: Simple Harmonic Motion- Analytic
- Page ID
- 25891
Our first example of a system that demonstrates simple harmonic motion is a springobject system on a frictionless surface, shown in Figure 23.2
The object is attached to one end of a spring. The other end of the spring is attached to a wall at the left in Figure 23.2. Assume that the object undergoes one-dimensional motion. The spring has a spring constant k and equilibrium length \(l_{e q}\) Choose the origin at the equilibrium position and choose the positive x -direction to the right in the Figure 23.2. In the figure, \(x>0\) corresponds to an extended spring, and \(x<0\) to a compressed spring. Define x(t) to be the position of the object with respect to the equilibrium position. The force acting on the spring is a linear restoring force, \(F_{x}=-k x\) (Figure 23.3). The initial conditions are as follows. The spring is initially stretched a distance \(l_{0}\) and given some initial speed \(v_{0}\) to the right away from the equilibrium position. The initial position of the stretched spring from the equilibrium position (our choice of origin) is \(x_{0}=\left(l_{0}-l_{e q}\right)>0\) and its initial x -component of the velocity is \(v_{x, 0}=v_{0}>0\).
Newton’s Second law in the x -direction becomes
\[-k x=m \frac{d^{2} x}{d t^{2}} \nonumber \]
This equation of motion, Equation (23.2.1), is called the simple harmonic oscillator equation (SHO). Because the spring force depends on the distance x , the acceleration is not constant. Equation (23.2.1) is a second order linear differential equation, in which the second derivative of the dependent variable is proportional to the negative of the dependent variable,
\[\frac{d^{2} x}{d t^{2}}=-\frac{k}{m} x \nonumber \]
In this case, the constant of proportionality is k/m.
Equation (23.2.2) can be solved from energy considerations or other advanced techniques but instead we shall first guess the solution and then verify that the guess satisfies the SHO differential equation (see Appendix 22.3.A for a derivation of the solution).
We are looking for a position function x(t) such that the second time derivative position function is proportional to the negative of the position function. Since the sine and cosine functions both satisfy this property, we make a preliminary ansatz (educated guess) that our position function is given by
\[x(t)=A \cos ((2 \pi / T) t)=A \cos \left(\omega_{0} t\right) \nonumber \]
where \(\omega_{0}\) is the angular frequency (as of yet, undetermined).
We shall now find the condition that the angular frequency \(\omega_{0}\) must satisfy in order to insure that the function in Equation (23.2.3) solves the simple harmonic oscillator equation, Equation (23.2.1). The first and second derivatives of the position function are given by
\[\begin{array}{l}
\frac{d x}{d t}=-\omega_{0} A \sin \left(\omega_{0} t\right) \\
\frac{d^{2} x}{d t^{2}}=-\omega_{0}^{2} A \cos \left(\omega_{0} t\right)=-\omega_{0}^{2} x
\end{array} \nonumber \]
Substitute the second derivative, the second expression in Equation (23.2.4), and the position function, Equation (23.2.3), into the SHO Equation (23.2.1), yielding
\[-\omega_{0}^{2} A \cos \left(\omega_{0} t\right)=-\frac{k}{m} A \cos \left(\omega_{0} t\right) \nonumber \]
Equation (23.2.5) is valid for all times provided that
\[\omega_{0}=\sqrt{\frac{k}{m}} \nonumber \]
The period of oscillation is then
\[T=\frac{2 \pi}{\omega_{0}}=2 \pi \sqrt{\frac{m}{k}} \nonumber \]
One possible solution for the position of the block is
\[x(t)=A \cos (\sqrt{\frac{k}{m}} t) \nonumber \]
and therefore by differentiation, the x -component of the velocity of the block is
\[v_{x}(t)=-\sqrt{\frac{k}{m}} A \sin (\sqrt{\frac{k}{m}} t) \nonumber \]
Note that at \(t=0\), the position of the object is \(x_{0} \equiv x(t=0)=A\) since \(\cos (0)=1\) and the velocity is \(v_{x, 0} \equiv v_{x}(t=0)=0\) since \(\sin (0)=0\). The solution in (23.2.8) describes an object that is released from rest at an initial position \(A=x_{0}\), but does not satisfy the initial velocity condition, \(v_{x}(t=0)=v_{x, 0} \neq 0\). We can try a sine function as another possible solution,
\[x(t)=B \sin (\sqrt{\frac{k}{m}} t) \nonumber \]
This function also satisfies the simple harmonic oscillator equation because
\[\frac{d^{2} x}{d t^{2}}=-\frac{k}{m} B \sin (\sqrt{\frac{k}{m}} t)=-\omega_{0}^{2} x \nonumber \]
where \(\omega_{0}=\sqrt{k / m}\). The x -component of the velocity associated with Equation (23.2.10) is
\[v_{x}(t)=\frac{d x}{d t}=\sqrt{\frac{k}{m}} B \cos (\sqrt{\frac{k}{m}} t) \nonumber \]
The proposed solution in Equation (23.2.10) has initial conditions \(x_{0} \equiv x(t=0)=0\) and \(v_{x, 0} \equiv v_{x}(t=0)=(\sqrt{k / m}) B\), thus \(B=v_{x, 0} / \sqrt{k / m}\) This solution describes an object that is initially at the equilibrium position but has an initial non-zero x -component of the velocity, \(v_{x, 0} \neq 0\)
General Solution of Simple Harmonic Oscillator Equation
Suppose \(x_{1}(t)\) and \(x_{2}(t)\) are both solutions of the simple harmonic oscillator equation,
\[\begin{array}{l}
\frac{d^{2}}{d t^{2}} x_{1}(t)=-\frac{k}{m} x_{1}(t) \\
\frac{d^{2}}{d t^{2}} x_{2}(t)=-\frac{k}{m} x_{2}(t)
\end{array} \nonumber \]
Then the sum \(x(t)=x_{1}(t)+x_{2}(t)\) of the two solutions is also a solution. To see this, consider
\[\frac{d^{2} x(t)}{d t^{2}}=\frac{d^{2}}{d t^{2}}\left(x_{1}(t)+x_{2}(t)\right)=\frac{d^{2} x_{1}(t)}{d t^{2}}+\frac{d^{2} x_{2}(t)}{d t^{2}} \nonumber \]
Using the fact that \(x_{1}(t)\) and \(x_{2}(t)\) both solve the simple harmonic oscillator equation (23.2.13), we see that
\[\begin{aligned}
\frac{d^{2}}{d t^{2}} x(t) &=-\frac{k}{m} x_{1}(t)+-\frac{k}{m} x_{2}(t)=-\frac{k}{m}\left(x_{1}(t)+x_{2}(t)\right) \\
&=-\frac{k}{m} x(t)
\end{aligned} \nonumber \]
Thus the linear combination \(x(t)=x_{1}(t)+x_{2}(t)\) is also a solution of the SHO equation, Equation (23.2.1). Therefore the sum of the sine and cosine solutions is the general solution,
\[x(t)=C \cos \left(\omega_{0} t\right)+D \sin \left(\omega_{0} t\right) \nonumber \]
where the constant coefficients C and D depend on a given set of initial conditions \(x_{0} \equiv x(t=0) \text { and } v_{x, 0} \equiv v_{x}(t=0)\) where \(x_{0}\) and \(v_{x, 0}\) are constants. For this general solution, the x -component of the velocity of the object at time t is then obtained by differentiating the position function,
\[v_{x}(t)=\frac{d x}{d t}=-\omega_{0} C \sin \left(\omega_{0} t\right)+\omega_{0} D \cos \left(\omega_{0} t\right) \nonumber \]
To find the constants C and D , substitute t = 0 into the Equations (23.2.16) and (23.2.17). Because \(\cos (0)=1 \text { and } \sin (0)=0\), the initial position at time t = 0 is
\[x_{0} \equiv x(t=0)=C \nonumber \]
The x -component of the velocity at time t = 0 is
\[v_{x, 0}=v_{x}(t=0)=-\omega_{0} C \sin (0)+\omega_{0} D \cos (0)=\omega_{0} D \nonumber \]
Thus
\[C=x_{0} \text { and } D=\frac{v_{x, 0}}{\omega_{0}} \nonumber \]
and the x -component of the velocity of the object-spring system is
\[v_{x}(t)=-\sqrt{\frac{k}{m}} x_{0} \sin (\sqrt{\frac{k}{m}} t)+v_{x, 0} \cos (\sqrt{\frac{k}{m}} t) \nonumber \]
Although we had previously specified \(x_{0}>0 \text { and } v_{x, 0}>0\), Equation (23.2.21) is seen to be a valid solution of the SHO equation for any values of \(x_{0}\) and \(v_{x, 0}\).
Example 23.1: Phase and Amplitude
Show that \(x(t)=C \cos \omega_{0} t+D \sin \omega_{0} t=A \cos \left(\omega_{0} t+\phi\right)\), where \(A=\left(C^{2}+D^{2}\right)^{1 / 2}>0\) and \(\phi=\tan ^{-1}(-D / C)\)
Solution: Use the identity \(A \cos \left(\omega_{0} t+\phi\right)=A \cos \left(\omega_{0} t\right) \cos (\phi)-A \sin \left(\omega_{0} t\right) \sin (\phi)\). Thus \(C \cos \left(\omega_{0} t\right)+D \sin \left(\omega_{0} t\right)=A \cos \left(\omega_{0} t\right) \cos (\phi)-A \sin \left(\omega_{0} t\right) \sin (\phi)\) Comparing coefficients we see that \(C=A \cos \phi \text { and } D=-A \sin \phi\). Therefore
\[\left(C^{2}+D^{2}\right)^{1 / 2}=A^{2}\left(\cos ^{2} \phi+\sin ^{2} \phi\right)=A^{2} \nonumber \]
We choose the positive square root to ensure that \(A>0\), and thus
\[\begin{array}{c}
A=\left(C^{2}+D^{2}\right)^{1 / 2} \\
\tan \phi=\frac{\sin \phi}{\cos \phi}=\frac{-D / A}{C / A}=-\frac{D}{C}
\end{array} \nonumber \]
\[\phi=\tan ^{-1}(-D / C) \nonumber \]
Thus the position as a function of time can be written as
\[x(t)=A \cos \left(\omega_{0} t+\phi\right) \nonumber \]
In Equation (23.2.25) the quantity \(\omega_{0} t+\phi\) is called the phase, and \(\phi\) is called the phase constant. Because \(\cos \left(\omega_{0} t+\phi\right)\) varies between +1 and −1 , and \(A>0\) A is the amplitude defined earlier. We now substitute Equation (23.2.20) into Equation (23.2.23) and find that the amplitude of the motion described in Equation (23.2.21), that is, the maximum value of x(t), and the phase are given by
\[A=\sqrt{x_{0}^{2}+\left(v_{x, 0} / \omega_{0}\right)^{2}} \nonumber \]
\[\phi=\tan ^{-1}\left(-v_{x, 0} / \omega_{0} x_{0}\right) \nonumber \]
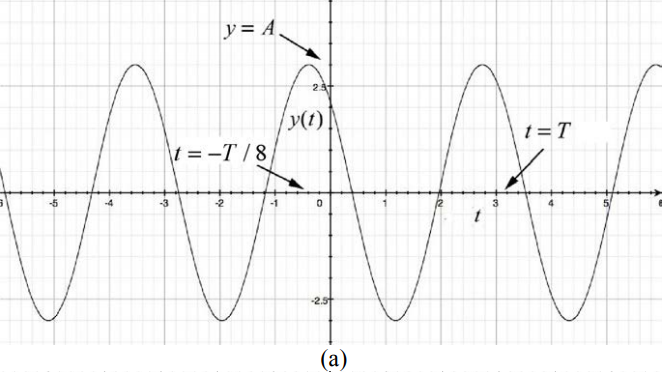
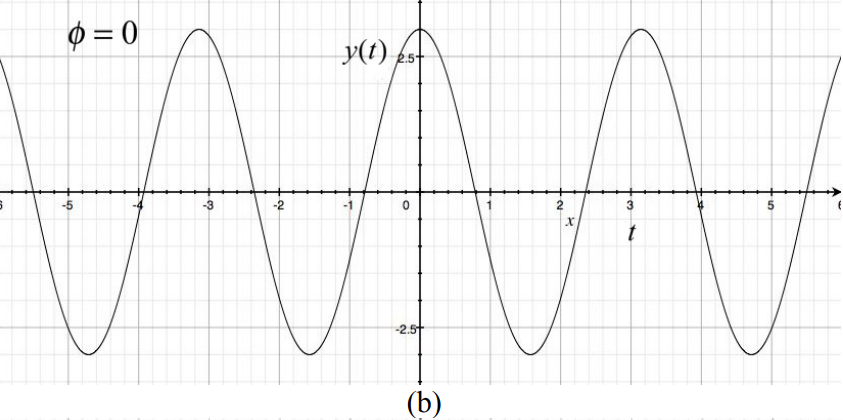
A plot of x t( ) vs. t is shown in Figure 23.4a with the values \(A=3, T=\pi\) and \(\phi=\pi / 4\). Note that \(x(t)=A \cos \left(\omega_{0} t+\phi\right)\) takes on its maximum value when \(\cos \left(\omega_{0} t+\phi\right)=1\). This occurs when \(\omega_{0} t+\phi=2 \pi n\) where \(n=0,\pm 1,\pm 2, \cdots\) The maximum value associated with n = 0 occurs when \(\omega_{0} t+\phi=0 \text { or } t=-\phi / \omega_{0}\). For the case shown in Figure 23.4a where \(\phi=\pi / 4\) this maximum occurs at the instant \(t=-T / 8\) Let’s plot \(x(t)=A \cos \left(\omega_{0} t+\phi\right)\) vs. t . Notice that when \(\phi>0, x(t)\) is shifted to the left compared with the case \(\phi=0\) (compare Figures 23.4a with 23.4b). The function \(x(t)=A \cos \left(\omega_{0} t+\phi\right)\) with \(\phi>0\) reaches its maximum value at an earlier time than the function \(x(t)=A \cos \left(\omega_{0} t\right)\). The difference in phases for these two cases is \(\left(\omega_{0} t+\phi\right)-\omega_{0} t=\phi\) and \(\phi\) is sometimes referred to as the phase shift. When \(\phi<0\) the, function \(x(t)=A \cos \left(\omega_{0} t+\phi\right)\) reaches its maximum value at a later time \(t=T / 8\) than the function \(x(t)=A \cos \left(\omega_{0} t\right)\) as shown in Figure 23.4c.
Example 23.2: Block-Spring System
A block of mass m is attached to a spring with spring constant k and is free to slide along a horizontal frictionless surface. At t = 0 , the block-spring system is stretched an amount \(x_{0}>0\) from the equilibrium position and is released from rest, \(v_{x, 0}=0\). What is the period of oscillation of the block? What is the velocity of the block when it first comes back to the equilibrium position?
Solution: The position of the block can be determined from Equation (23.2.21) by substituting the initial conditions \(x_{0}>0, \text { and } v_{x, 0}=0\) yielding
\[x(t)=x_{0} \cos (\sqrt{\frac{k}{m}} t) \nonumber \]
and the x -component of its velocity is given by Equation (23.2.22),
\[v_{x}(t)=-\sqrt{\frac{k}{m}} x_{0} \sin (\sqrt{\frac{k}{m}} t) \nonumber \]
The angular frequency of oscillation is \(\omega_{0}=\sqrt{k / m}\) and the period is given by Equation (23.2.7),
\[T=\frac{2 \pi}{\omega_{0}}=2 \pi \sqrt{\frac{m}{k}} \nonumber \]
The block first reaches equilibrium when the position function first reaches zero. This occurs at time \(t_{1}\) satisfying
\[\sqrt{\frac{k}{m}} t_{1}=\frac{\pi}{2}, \quad t_{1}=\frac{\pi}{2} \sqrt{\frac{m}{k}}=\frac{T}{4} \nonumber \]
The x -component of the velocity at time \(t_{1}\) is then
\[v_{x}\left(t_{1}\right)=-\sqrt{\frac{k}{m}} x_{0} \sin \left(\sqrt{\frac{k}{m}} t_{1}\right)=-\sqrt{\frac{k}{m}} x_{0} \sin (\pi / 2)=-\sqrt{\frac{k}{m}} x_{0}=-\omega_{0} x_{0} \nonumber \]
Note that the block is moving in the negative x -direction at time \(t_{1}\); the block has moved from a positive initial position to the equilibrium position (Figure 23.4(b)).