23.5: Damped Oscillatory Motion

Let’s now consider our spring-block system moving on a horizontal frictionless surface but now the block is attached to a damper that resists the motion of the block due to viscous friction. This damper, commonly called a dashpot, is shown in Figure 23.13. The viscous force arises when objects move through fluids at speeds slow enough so that there is no turbulence. When the viscous force opposes the motion and is proportional to the velocity, so that

\[\overrightarrow{\mathbf{f}}_{\mathrm{vis}}=-b \overrightarrow{\mathbf{v}} \nonumber \]

the dashpot is referred to as a linear dashpot. The constant of proportionality b depends on the properties of the dashpot.

Figure 23.12 Spring-block system connected to a linear dashpot

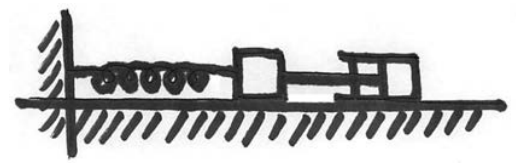
Choose the origin at the equilibrium position and choose the positive x -direction to the right in the Figure 23.13. Define \(x(t)\) to be the position of the object with respect to the equilibrium position. The x -component of the total force acting on the spring is the sum of the linear restoring spring force, and the viscous friction force (Figure 23.13),

\[F_{x}=-k x-b \frac{d x}{d t} \nonumber \]

Figure 23.13 Free-body force diagram for spring-object system with linear dashpot

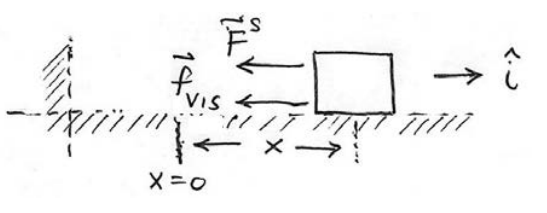
Newton’s Second law in the x -direction becomes

\[-k x-b \frac{d x}{d t}=m \frac{d^{2} x}{d t^{2}} \nonumber \]

We can rewrite Equation (23.5.3) as

\[\frac{d^{2} x}{d t^{2}}+\frac{b}{m} \frac{d x}{d t}+\frac{k}{m} x=0 \nonumber \]

When \((b / m)^{2}<4 k / m\) the oscillator is called underdamped, and the solution to Equation (23.5.4) is given by

\[x(t)=x_{\mathrm{m}} e^{-\alpha t} \cos (\gamma t+\phi) \nonumber \]

where \(\gamma=\left(k / m-(b / 2 m)^{2}\right)^{1 / 2}\) is the angular frequency of oscillation, \(\alpha=b / 2 m\) is a parameter that measured the exponential decay of the oscillations, \(x_{\mathrm{m}}\), is a constant and \(\phi\) is the phase constant. Recall the undamped oscillator has angular frequency \(\omega_{0}=(k / m)^{1 / 2}\), so the angular frequency of the underdamped oscillator can be expressed as

\[\gamma=\left(\omega_{0}^{2}-\alpha^{2}\right)^{1 / 2} \nonumber \]

In Appendix 23B: Complex Numbers, we introduce complex numbers and use them to solve Equation(23.5.4) in Appendix 23C: Solution to the Underdamped Simple Harmonic Oscillator Equation.

The x -component of the velocity of the object is given by

\[v_{x}(t)=d x / d t=\left(-\gamma x_{\mathrm{m}} \sin (\gamma t+\phi)-\alpha x_{\mathrm{m}} \cos (\gamma t+\phi)\right) e^{-\alpha t} \nonumber \]

The position and the x -component of the velocity of the object oscillate but the amplitudes of the oscillations decay exponentially. In Figure 23.14, the position is plotted as a function of time for the underdamped system for the special case \(\phi=0\). For that case

\[x(t)=x_{\mathrm{m}} e^{-\alpha t} \cos (\gamma t) \nonumber \]

and

\[v_{x}(t)=d x / d t=\left(-\gamma x_{\mathrm{m}} \sin (\gamma t)-\alpha x_{\mathrm{m}} \cos (\gamma t)\right) e^{-\alpha t} \nonumber \]

Figure 23.14 Plot of position x(t) of object for underdamped oscillator with φ = 0

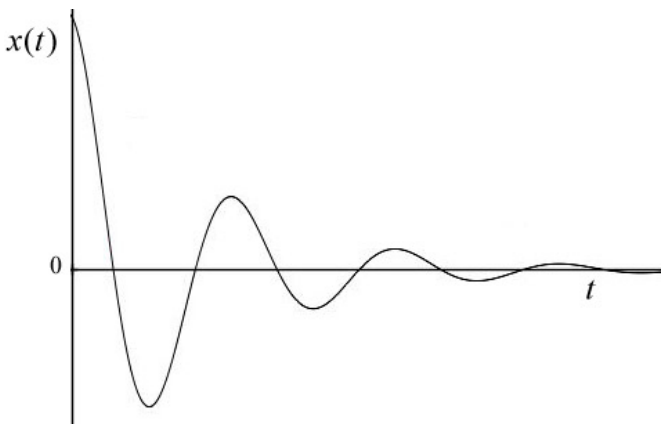
Because the coefficient of exponential decay \(\alpha=b / 2 m\) is proportional to the b, we see that the position will decay more rapidly if the viscous force increases. We can introduce a time constant

\[\tau=1 / \alpha=2 m / b \nonumber \]

When \(t=\tau\), the position is

\[x(t=\tau)=x_{\mathrm{m}} \cos (\gamma \tau) e^{-1} \nonumber \]

The envelope of exponential decay has now decreases by a factor of \(e^{-1}\), i.e. the amplitude can be at most \(x_{\mathrm{m}} e^{-1}\). During this time interval \([0, \tau]\) the position has undergone a number of oscillations. The total number of radians associated with those oscillations is given by

\[\gamma \tau=\left(k / m-(b / 2 m)^{2}\right)^{1 / 2}(2 m / b) \nonumber \]

The closest integral number of cycles is then

\[n=[\gamma \tau / 2 \pi]=\left[\left(k / m-(b / 2 m)^{2}\right)^{1 / 2}(m / \pi b)\right] \nonumber \]

If the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by

\[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \]

where \(\omega_{0}=(k / m)^{1 / 2}\) is the angular frequency of the undamped oscillator.

We define the quality, Q , of this oscillating system to be proportional to the number of integral cycles it takes for the exponential envelope of the position function to fall off by a factor of \(e^{-1}\). The constant of proportionality is chosen to be \(\pi\). Thus

\[Q=n \pi \nonumber \]

For the weakly damped case, we have that

\[Q \simeq \omega_{0}(m / b) \nonumber \]

Energy in the Underdamped Oscillator

For the underdamped oscillator, \((b / m)^{2}<4 k / m, \quad \gamma=\left(k / m-(b / 2 m)^{2}\right)^{1 / 2}\), and \(\alpha=b / 2 m\). Let’s choose \(t=0\) such that the phase shift is zero \(\phi=0\) The stored energy in the system will decay due to the energy loss due to dissipation. The mechanical energy stored in the potential and kinetic energies is then given by

\[E=\frac{1}{2} k x^{2}+\frac{1}{2} m v^{2} \nonumber \]

where the position and the x -component of the velocity are given by Equations (23.5.8) and (23.5.9). The mechanical energy is then

\[E=\frac{1}{2} k x_{\mathrm{m}}^{2} \cos ^{2}(\gamma t) e^{-2 \alpha t}+\frac{1}{2} m\left(-\gamma x_{\mathrm{m}} \sin (\gamma t)-\alpha x_{\mathrm{m}} \cos (\gamma t)\right)^{2} e^{-2 \alpha t} \nonumber \]

Expanding this expression yields

\[E=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \cos ^{2}(\gamma t) e^{-2 \alpha t}+m \gamma \alpha x_{\mathrm{m}}^{2} \sin (\gamma t) \cos (\gamma t) e^{-2 \alpha t}+\frac{1}{2} m \gamma^{2} x_{\mathrm{m}}^{2} \sin ^{2}(\gamma t) e^{-2 \alpha t} \nonumber \]

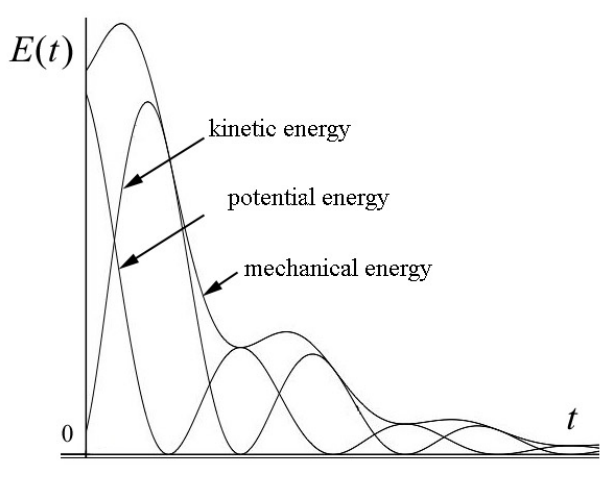
The kinetic energy, potential energy, and mechanical energy are shown in Figure 23.15.

Figure 23.15 Kinetic, potential and mechanical energy for the underdamped oscillator

The stored energy at time t = 0 is

\[E(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \]

The mechanical energy at the conclusion of one cycle, with \(\gamma T=2 \pi\), is

\[E(t=T)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} e^{-2 \alpha T} \nonumber \]

The change in the mechanical energy for one cycle is then

\[E(t=T)-E(t=0)=-\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2}\left(1-e^{-2 \alpha T}\right) \nonumber \]

Recall that \(\alpha^{2}=b^{2} / 4 m^{2}\). Therefore

\[E(t=T)-E(t=0)=-\frac{1}{2}\left(k+b^{2} / 4 m\right) x_{\mathrm{m}}^{2}\left(1-e^{-2 \alpha T}\right) \nonumber \]

We can show (although the calculation is lengthy) that the energy dissipated by the viscous force over one cycle is given by the integral

\[E_{\mathrm{dis}}=\int_{0}^{T} \overrightarrow{\mathbf{F}}_{\mathrm{vis}} \cdot \overrightarrow{\mathbf{v}} d t=-\left(k+\frac{b^{2}}{4 m}\right) \frac{x_{\mathrm{m}}^{2}}{2}\left(1-e^{-2 \alpha t}\right) \nonumber \]

By comparison with Equation (23.5.23), the change in the mechanical energy in the underdamped oscillator during one cycle is equal to the energy dissipated due to the viscous force during one cycle.