23.4: Worked Examples
- Page ID
- 25893
Example 23.3: Rolling Without Slipping Oscillating Cylinder
Attach a solid cylinder of mass M and radius R to a horizontal massless spring with spring constant k so that it can roll without slipping along a horizontal surface. At time t , the center of mass of the cylinder is moving with speed \(V_{c m}\) and the spring is compressed vθ ,1 = ± 2gl(1− cosθ0 ) . a distance x from its equilibrium length. What is the period of simple harmonic motion for the center of mass of the cylinder?
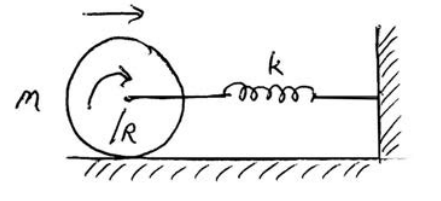
Solution: At time t , the energy of the rolling cylinder and spring system is
\[E=\frac{1}{2} M v_{c m}^{2}+\frac{1}{2} I_{c m}\left(\frac{d \theta}{d t}\right)^{2}+\frac{1}{2} k x^{2} \nonumber \]
where x is the amount the spring has compressed, \(I_{c m}=(1 / 2) M R^{2}\), and because it is rolling without slipping
\[\frac{d \theta}{d t}=\frac{V_{c m}}{R} \nonumber \]
Therefore the energy is
\[E=\frac{1}{2} M V_{c m}^{2}+\frac{1}{4} M R^{2}\left(\frac{V_{c m}}{R}\right)^{2}+\frac{1}{2} k x^{2}=\frac{3}{4} M V_{c m}^{2}+\frac{1}{2} k x^{2} \nonumber \]
The energy is constant (no non-conservative force is doing work on the system) so
\[0=\frac{d E}{d t}=\frac{3}{4} 2 M V_{c m} \frac{d V_{c m}}{d t}+\frac{1}{2} k 2 x \frac{d x}{d t}=V_{c m}\left(\frac{3}{2} M \frac{d^{2} x}{d t^{2}}+k x\right) \nonumber \]
Because \(V_{c m}\) is non-zero most of the time, the displacement of the spring satisfies a simple harmonic oscillator equation
\[\frac{d^{2} x}{d t^{2}}+\frac{2 k}{3 M} x=0 \nonumber \]
Hence the period is
\[T=\frac{2 \pi}{\omega_{0}}=2 \pi \sqrt{\frac{3 M}{2 k}} \nonumber \]
Example 23.4: U-Tube
A U-tube open at both ends is filled with an incompressible fluid of density \(\rho\). The cross-sectional area A of the tube is uniform and the total length of the fluid in the tube is L . A piston is used to depress the height of the liquid column on one side by a distance \(x_{0}\) (raising the other side by the same distance) and then is quickly removed (Figure 23.10). What is the angular frequency of the ensuing simple harmonic motion? Neglect any resistive forces and at the walls of the U-tube.
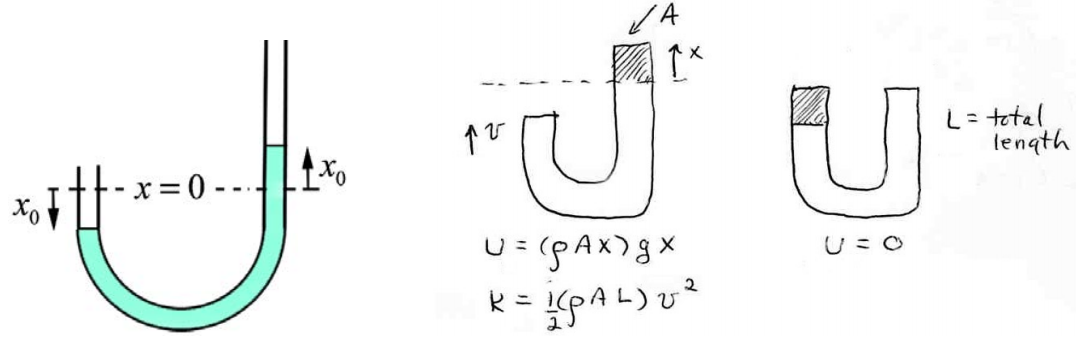
Solution: We shall use conservation of energy. First choose as a zero for gravitational potential energy in the configuration where the water levels are equal on both sides of the tube. When the piston on one side depresses the fluid, it rises on the other. At a given instant in time when a portion of the fluid of mass \(\Delta m=\rho A x\) is a height x above the equilibrium height (Figure 23.11), the potential energy of the fluid is given by
\[U=\Delta m g x=(\rho A x) g x=\rho \operatorname{Ag} x^{2} \nonumber \]
At that same instant the entire fluid of length L and mass \(m=\rho A L\) is moving with speed v , so the kinetic energy is
\[K=\frac{1}{2} m v^{2}=\frac{1}{2} \rho A L v^{2} \nonumber \]
Thus the total energy is
\[E=K+U=\frac{1}{2} \rho A L v^{2}+\rho A g x^{2} \nonumber \]
By neglecting resistive force, the mechanical energy of the fluid is constant. Therefore
\[0=\frac{d E}{d t}=\rho A L v \frac{d v}{d t}+2 \rho \operatorname{Ag} x \frac{d x}{d t} \nonumber \]
If we just consider the top of the fluid above the equilibrium position on the right arm in Figure 23.13, we rewrite Equation (23.4.10) as
\[0=\frac{d E}{d t}=\rho A L v_{x} \frac{d v_{x}}{d t}+2 \rho A g x \frac{d x}{d t} \nonumber \]
where \(v_{x}=d x / d t\). We now rewrite the energy condition using \(d v_{x} / d t=d^{2} x / d t^{2}\) as
\[0=v_{x} \rho A\left(L \frac{d^{2} x}{d t^{2}}+2 g x\right) \nonumber \]
This condition is satisfied when \(v_{x}=0\) i.e. the equilibrium condition or when
\[0=L \frac{d^{2} x}{d t^{2}}+2 g x \nonumber \]
This last condition can be written as
\[\frac{d^{2} x}{d t^{2}}=-\frac{2 g}{L} x \nonumber \]
This last equation is the simple harmonic oscillator equation. Using the same mathematical techniques as we used for the spring-block system, the solution for the height of the fluid above the equilibrium position is given by
\[x(t)=B \cos \left(\omega_{0} t\right)+C \sin \left(\omega_{0} t\right) \nonumber \]
where
\[\omega_{0}=\sqrt{\frac{2 g}{L}} \nonumber \]
is the angular frequency of oscillation. The x -component of the velocity of the fluid on the right-hand side of the U-tube is given by
\[v_{x}(t)=\frac{d x(t)}{d t}=-\omega_{0} B \sin \left(\omega_{0} t\right)+\omega_{0} C \cos \left(\omega_{0} t\right) \nonumber \]
The coefficients B and C are determined by the initial conditions. At \(t=0\) the height of the fluid is \(x(t=0)=B=x_{0}\). At \(t=0\), the speed is zero so \(v_{x}(t=0)=\omega_{0} C=0\), hence \(C=0\). The height of the fluid above the equilibrium position on the right hand-side of the U-tube as a function of time is thus
\[x(t)=x_{0} \cos (\sqrt{\frac{2 g}{L}} t) \nonumber \]