8.7: Exercise Problems

Last updated
Save as PDF

Page ID: 34801

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

8.1. Find the first-order correction to the Pascal equation (6) for a liquid, due to its low but nonzero compressibility, and evaluate this correction for the water at the bottom of the Earth’s oceans.

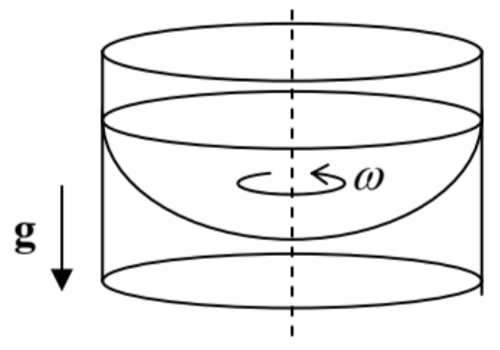
8.2. Find the stationary shape of the open surface of an incompressible, heavy fluid in a container rotated about its vertical axis with a constant angular velocity \(\omega\) - see the figure on the right.

Screen Shot 2022-01-28 at 11.14.23 PM.png

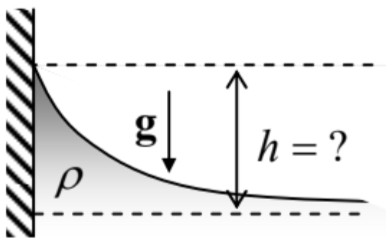
8.3.* Use two different approaches to calculate the stationary shape of the surface of an incompressible fluid of density \(\rho\) near a vertical plane wall, in a uniform gravity field - see the figure on the right. In particular, find the height \(h\) of liquid’s rise at the wall surface as a function of the contact angle \(\theta_{c}\).

Screen Shot 2022-01-28 at 11.15.33 PM.png

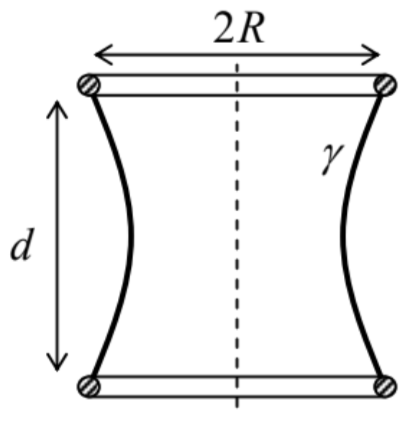
8.4. \(^{*}\) A soap film with surface tension \(\gamma\) is stretched between two similar, coaxial, thin, round rings of radius \(R\), separated by distance \(d\) - see the figure on the right. Neglecting gravity, calculate the equilibrium shape of the film, and the force needed for keeping the rings at the fixed distance.

Screen Shot 2022-01-28 at 11.16.34 PM.png

8.5. A solid sphere of radius \(R\) is kept in a steady, vorticity-free flow of an ideal incompressible fluid, with velocity \(v_{0}\). Find the spatial distribution of velocity and pressure, and in particular their extreme values. Compare the results with those obtained in Sec. 4 for a round cylinder.

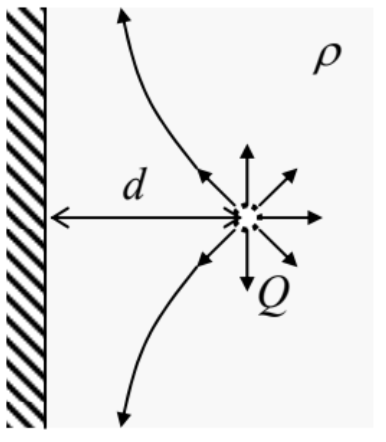
8.6. A small source, located at distance \(d\) from a plane wall of a container filled with an ideal, incompressible fluid of density \(\rho\), injects additional fluid isotropically, at a constant mass current ("discharge") \(Q \equiv d M / d t-\) see the figure on the right. Calculate the fluid’s velocity distribution, and its pressure on the

Hint: Recall the charge image method in electrostatics, \({ }^{51}\) and contemplate its possible analog.

Screen Shot 2022-01-28 at 11.19.07 PM.png

8.7. Calculate the average kinetic, potential, and full energies (per unit area) of a traveling sinusoidal wave, of a small amplitude \(q_{A}\), on the horizontal surface on an ideal, incompressible, deep fluid of density \(\rho\), in a uniform gravity field \(\mathbf{g}\).

8.8. Calculate the average power (per unit width of wave’s front) carried by the surface wave discussed in the previous problem, and relate the result to the wave’s energy.

8.9. Derive Eq. (48) for the surface waves on a finite-thickness layer of a heavy liquid.

8.10. Derive Eq. (50) for the capillary waves ("ripples").

8.11 .* Derive a \(2 \mathrm{D}\) differential equation describing the propagation of relatively long \((\lambda>>h)\) waves on the surface of a broad, plane layer of thickness \(h\), of an ideal, incompressible fluid, and use it to calculate the longest standing wave modes and frequencies in a layer covering a spherical planet of radius \(R \gg>\) h.

Hint: The second task requires some familiarity with the basic properties of spherical harmonics. \({ }^{52}\)

8.12. Calculate the velocity distribution and the dispersion relation of the waves propagating along the horizontal interface of two ideal, incompressible fluids of different densities.

8.13. Use the finite-difference approximation for the Laplace operator, with the mesh step \(h=\) \(a / 4\), to find the maximum velocity and total mass flow \(Q\) of a viscous, incompressible fluid through a long pipe with a square-shaped cross-section of side \(a\). Compare the results with those described in Sec. 5 for the same problem with the mesh step \(h=a / 2\), and for a pipe with the circular cross-section of the same area.

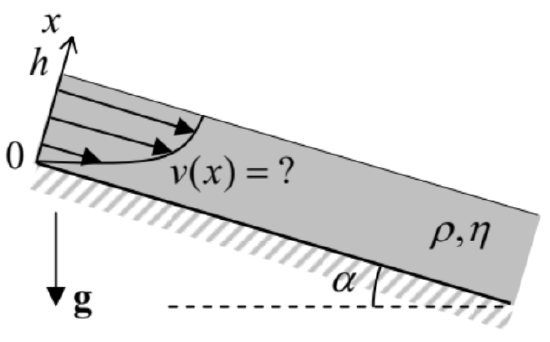
8.14. A layer, of thickness \(h\), of a heavy, viscous, incompressible fluid flows down a long and wide inclined plane, under its own weight - see the figure on the right. Find the stationary velocity distribution profile, and the total fluid discharge (per unit width.)

Screen Shot 2022-01-28 at 11.20.20 PM.png

8.15. Calculate the drag torque exerted on a unit length of a solid round cylinder of radius \(R\) that rotates about its axis, with angular velocity \(\omega\), inside an incompressible fluid with viscosity \(\eta\), kept static far from the cylinder.

8.16. Calculate the tangential force (per unit area) exerted by an incompressible fluid, with density \(\rho\) and viscosity \(\eta\), on a broad solid plane placed over its surface and forced to oscillate, along the surface, with amplitude \(a\) and frequency \(\omega\).

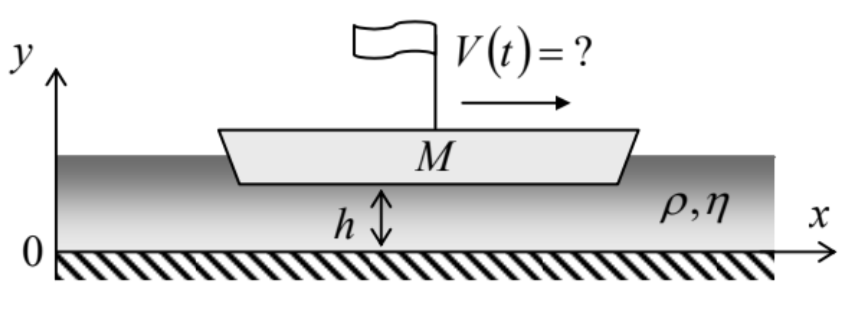
8.17. A massive barge, with a flat bottom of area \(A\), floats in shallow water, with clearance \(h \ll A^{1 / 2}-\) see the figure on the right. Analyze the time dependence of the barge’s velocity \(V(t)\), and the water velocity profile, after the barge’s engine has been turned off. Discuss the limits of large and small values of the dimensionless parameter \(M / \rho A h\).

Screen Shot 2022-01-28 at 11.21.20 PM.png

8.18. * Derive a general expression for mechanical energy loss rate in a viscous incompressible fluid that obeys the Navier-Stokes equation, and use this expression to calculate the attenuation coefficient of the surface waves, assuming that the viscosity is small. (Quantify this condition).

8.19. Use the Navier-Stokes equation to calculate the coefficient of attenuation of a plane, sinusoidal acoustic wave.

\({ }^{51}\) See, e.g., EM Secs. 2.9, 3.3, and 4.3.

\({ }^{52}\) See, e.g., EM Sec. \(2.8\) and/or QM Sec. 3.6.