12.7: Bohr’s Theory of the Hydrogen Atom
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Describe early atomic models.
- Explain Bohr’s theory of the hydrogen atom.
- Distinguish between correct and incorrect features of the Bohr model, in light of modern quantum mechanics.
The great Danish physicist Niels Bohr (1885–1962) made immediate use of Rutherford’s planetary model of the atom. (Figure \PageIndex{1}). Bohr became convinced of its validity and spent part of 1912 at Rutherford’s laboratory. In 1913, after returning to Copenhagen, he began publishing his theory of the simplest atom, hydrogen, based on the planetary model of the atom. For decades, many questions had been asked about atomic characteristics. From their sizes to their spectra, much was known about atoms, but little had been explained in terms of the laws of physics. Bohr’s theory explained the atomic spectrum of hydrogen and established new and broadly applicable principles in quantum mechanics.

Atomic Spectra
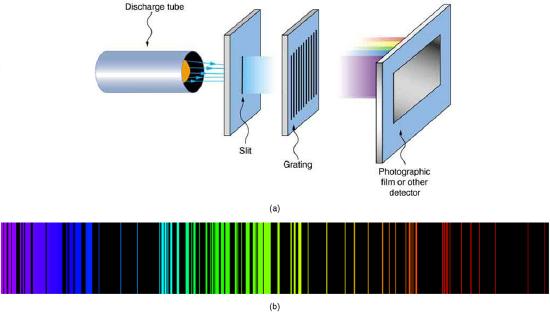
Atomic and molecular emission and absorption spectra have been known for over a century to be discrete (or quantized). Well before they were understood from first principles, chemists have been using the emission and absorption spectra for identification of elements. Figure \PageIndex{2} shows iron emission spectrum, for example. No other elements emit the exactly the same set of frequencies of light. With the discovery of substructure of the atom and the discovery of photon (or more precisely, refined understanding of the particle nature of electromagnetic waves where the particle energy is proportional to the frequency of electromagnetic waves), these resonant frequencies of light emitted by atoms could be used to infer an atomic model.
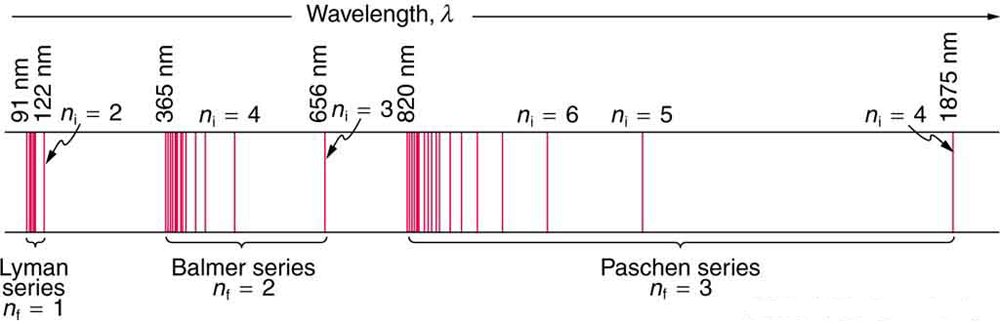
For the hydrogen atom, the lightest element with the simplest atom, a pattern for its line spectrum was noticed by experimentalists (see Figure \PageIndex{3}). All wavelengths of the line spectrum could be described by a following formula, for the suitable choice of two integers n_{i} and n_{f}:
\frac{1}{\lambda}=R\left(\frac{1}{n_{\mathrm{f}}^{2}}-\frac{1}{n_{\mathrm{i}}^{2}}\right), \label{1}
where \lambda is the wavelength of the emitted EM radiation and R is the Rydberg constant, determined by the experiment to be
R=1.097 \times 10^{7} / \mathrm{m}\left(\text { or } \mathrm{m}^{-1}\right). \nonumber
The n_{\mathrm{f}} is a positive integer associated with a specific series, which are named after their discoverers. For the Lyman series, n_{\mathrm{f}}=1; for the Balmer series, n_{\mathrm{f}}=2; for the Paschen series, n_{\mathrm{f}}=3; and so on. The Lyman series is entirely in the UV, while part of the Balmer series is visible with the remainder UV. The Paschen series and all the rest are entirely IR. There are apparently an unlimited number of series, although they lie progressively farther into the infrared and become difficult to observe as \n_{\mathrm{f}} increases. The n_{\mathrm{i}} is a positive integer greater than n_{\mathrm{f}}. So for example, for the Balmer series, n_{\mathrm{f}}=2 and n_{\mathrm{i}}=3,4,5,6, \ldots.
So, before Bohr's model of the hydrogen atom, such was the picture of atomic theory—full of suggestive (and even well-organized) data and no unifying explanation. Ernest Rutherford is quoted as saying, "All science is either physics or stamp-collecting." What he meant is, there are branches of science whose practitioners would be satisfied with a collection of interesting facts (i.e. "stamp-collecting"). But what makes physics physics is the search for the theoretical framework providing explanations based on fundamental principles, not idiosyncratic descriptions. Bohr's model brought the science of spectroscopy into physics.
Bohr's Model for Hydrogen
The planetary model of the atom suggested by Rutherford was in trouble. While the model provided a possible picture of how the very small atomic nucleus might be arranged with the electrons in a stable arrangement, it did not provide for the size of electron orbits (which would be related to the size of the atom), and the arrangement was not actually stable—an orbiting electron is an oscillating charge; an oscillating charge emits electromagnetic waves; electromagnetic waves carry away energy; so as the electron loses energy, it would fall into the proton. By some estimates, this would occur in as short a time as 10^{-7} \mathrm{~s}!
Bohr's starting point for his successful model was this: he proposed that the orbits of electrons in atoms are quantized. To fully understand this statement, we can compare the orbits of electrons in atoms to the orbits of planets in the solar system. The orbits of planets are not quantized. While laws of physics govern how planets move in the solar system (see for example, Kepler's laws, or their derivation by Newton starting with the inverse-square law of gravitation), there is no law of physics dictating how far each body in the solar system must be from the Sun. So the orbits of planets are not quantized.
So what Bohr was proposing was an entirely new law of physics no one had known before. In one sense, it was not completely new (Planck and Einstein already enjoyed some successes from suggesting quantization of energy in thermal oscillators and EM radiation); in another sense, it was a big break from centuries of classical mechanics. This was Bohr's quantization rule: angular momentum of an electron in its orbit is quantized. In mathematical form,
L=n \hbar, \nonumber
where nn could take on any positive integer value (n=1,2,3, \ldots), and \hbar is known as the reduced Planck constant (\hbar=h / 2 \pi). And angular momentum, L, as you might remember from earlier chapter, is given by the following for a particle in a uniform circular orbit: L=m v r, where m is the mass of the particle, v is the speed of the particle in orbit, and rr is the radius of circular orbit. Using this as the starting point, semiclassical analysis of orbital motion yields a whole array of quantized (i.e. allowed) values of orbital distance \left(r_{n}\right), orbital speed \left(v_{n}\right), and orbital energy \left(E_{n}\right), among others (see: Table \PageIndex{1} for a summary).
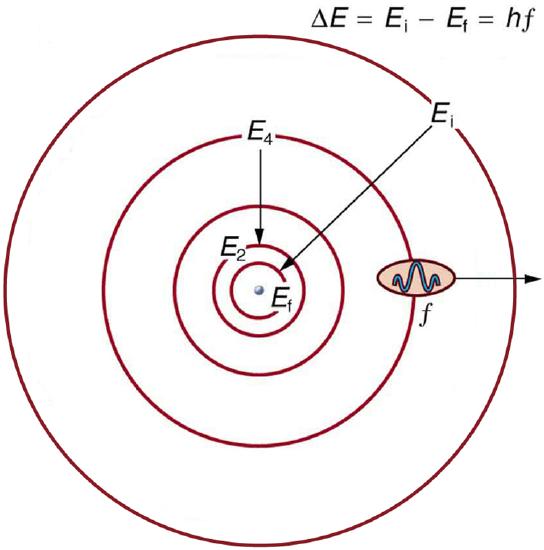
With the quantized orbital energies for the electron, we have a ready explanation for the features of atomic spectra. EM radiation is emitted when an electron transitions from a higher energy level (E_{i}) to a lower energy level (E_{f}), with the photon carrying away the energy difference,
h f=\Delta E=E_{i}-E_{f}, \label{2}
where f is the frequency of the photon. Figure \PageIndex{4} shows a schematic representation of this relationship. With only discrete values of energy E_{n} allowed, there are only discrete values of frequency (f) and wavelength (\lambda) allowed also, as shown in the line spectra.
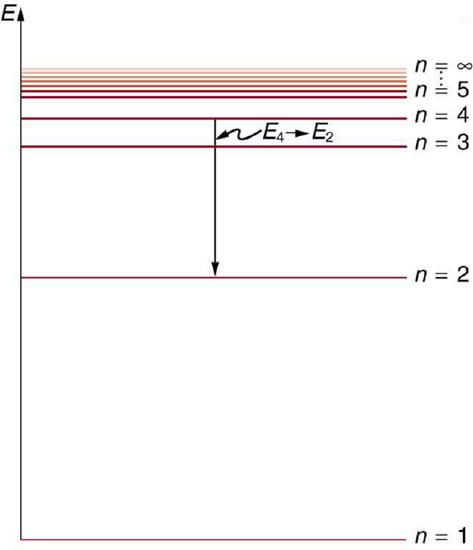
Energy-level diagram, shown in Figure \PageIndex{5}, is another convenient way to illustrate these relationships. Allowed energy levels for the atom are plotted vertically with the lowest state (or ground state) at the bottom and with excited states above that. The energies of the lines in an atomic spectrum correspond to the differences in energy levels in the level diagram (figure illustrates a transition from E_{4} to E_{2}, which would show up in the atomic spectrum as one line).
| Quantized quantity | Dependence on quantum number n | Full expression |
|---|---|---|
| angular momentum: L_{n} | proportional to n | L_{n}=n \hbar |
| orbital radius: r_{n} | proportional to n^{2} | r_{n}=\frac{n^{2} \hbar^{2}}{m k e^{2}} |
| orbital speed: v_{n} | proportional to \frac{1}{n} | v_{n}=\frac{k e^{2}}{n \hbar} |
| orbital energy: E_{n} | proportional to \frac{1}{n^{2}} | E_{n}=-\frac{m k^{2} e^{4}}{2 n^{2} \hbar^{2}}=-\frac{13.6}{n^{2}} \mathrm{eV} |
Two key results are worth highlighting. The first is the Bohr radius, or the smallest orbital radius a, given for n=1,
\begin{align*} a &=r_{1}=\hbar^{2} / m k e^{2} \\ &=0.529 \times 10^{-10} \mathrm{~m}. \end{align*}
This is the Bohr model's prediction for the size of the atom, made with nothing more than electric constants, mass of the electron, and the Planck's constant, and this theoretical prediction matches experimentally measured sizes of atoms fairly well.
The second is the derivation of the Rydberg formula, first given in Equation \eqref{1}. To derive this, we start out with Equation \eqref{2} and substitute in expressions for hydrogen energies from Table \PageIndex{1}:
\begin{align*} h f &=-\frac{m k^{2} e^{4}}{2 n_{i}^{2} \hbar^{2}}-\left(-\frac{m k^{2} e^{4}}{2 n_{f}^{2} \hbar^{2}}\right) \\ &=\frac{m k^{2} e^{4}}{2 \hbar^{2}}\left(\frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{2}}\right) \end{align*}
Frequency f is equal to c / \lambda. Plugging this in and solving for 1 / \lambda while also replacing all instances of \hbar with h / 2 \pi, we get,
\frac{1}{\lambda}=\frac{2 \pi^{2} m k^{2} e^{4}}{h^{3} c}\left(\frac{1}{n_{f}}-\frac{1}{n_{i}}\right), \nonumber
which yields an analytical expression for the Rydberg constant,
R=\frac{2 \pi^{2} m k^{2} e^{4}}{h^{3} c}=1.097 \times 10^{7} \mathrm{~m}^{-1}. \nonumber
Figure \PageIndex{6} shows an energy-level diagram for hydrogen that also illustrates how the various spectral series for hydrogen are related to transitions between energy levels.
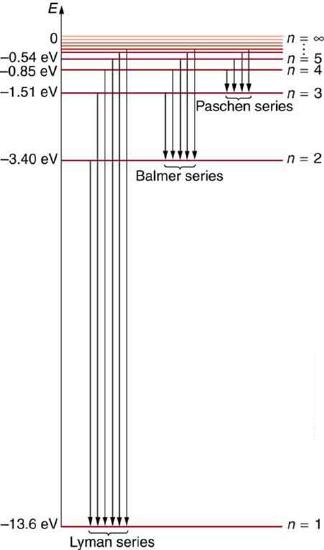
We see that Bohr’s theory of the hydrogen atom answers the question as to why this previously known formula describes the hydrogen spectrum. It is because the energy levels are proportional to 1 / n^{2}, where n is a non-negative integer. A downward transition releases energy, and so n_{\mathrm{i}} must be greater than n_{\mathrm{f}}. The various series are those where the transitions end on a certain level. For the Lyman series, n_{\mathrm{f}}=1 — that is, all the transitions end in the ground state (see also Figure \PageIndex{6}). For the Balmer series, n_{\mathrm{f}}=2, or all the transitions end in the first excited state; and so on. What was once a recipe is now based in physics, and something new is emerging—angular momentum is quantized.
Triumphs and Limits of the Bohr Theory
Bohr did what no one had been able to do before. Not only did he explain the spectrum of hydrogen, he correctly calculated the size of the atom from basic physics. Some of his ideas are broadly applicable. Electron orbital energies are quantized in all atoms and molecules. Angular momentum is quantized. The electrons do not spiral into the nucleus, as expected classically. These are major triumphs.
But there are limits to Bohr’s theory. It cannot be applied to multielectron atoms, even one as simple as a two-electron helium atom. Bohr’s model is a semiclassical model. The orbits are quantized (quantum mechanical) but are assumed to be simple circular paths (classical). As quantum mechanics was developed, it became clear that there are no well-defined orbits; rather, there are "clouds" of probability. Bohr’s theory also did not explain that some spectral lines are doublets (split into two) when examined closely. These deficiencies are addressed in later, fully-quantum-mechanical atomic models, but it should be kept in mind that Bohr did not fail. Rather, he made very important steps along the path to greater knowledge and laid the foundation.
Section Summary
- The planetary model of the atom pictures electrons orbiting the nucleus in the way that planets orbit the sun. Bohr used the planetary model to develop the first reasonable theory of hydrogen, the simplest atom. Atomic and molecular spectra are quantized, with hydrogen spectrum wavelengths given by the formula
\frac{1}{\lambda}=R\left(\frac{1}{n_{\mathrm{f}}^{2}}-\frac{1}{n_{\mathrm{i}}^{2}}\right), \nonumber
where \lambda is the wavelength of the emitted EM radiation and R is the Rydberg constant, which has the valueR=1.097 \times 10^{7} \mathrm{~m}^{-1}. \nonumber
- The constants n_{\mathrm{i}} and n_{\mathrm{f}} are positive integers, and n_{\mathrm{i}} must be greater than n_{\mathrm{f}}.
- Bohr correctly proposed that the energy and radii of the orbits of electrons in atoms are quantized, with energy for transitions between orbits given by
\Delta E=h f=E_{\mathrm{i}}-E_{\mathrm{f}}, \nonumber
-
where \Delta E is the change in energy between the initial and final orbits and hf is the energy of an absorbed or emitted photon. It is useful to plot orbital energies on a vertical graph called an energy-level diagram.
- Bohr proposed that the allowed orbits are circular and must have quantized orbital angular momentum given by
L=m_{e} v r_{n}=n \frac{h}{2 \pi}(n=1,2,3 \ldots), \nonumber
where L is the angular momentum, r_{n} is the radius of the n\mathrm{th} orbit, and h is Planck’s constant. - Additional quantized orbital quantities—orbital radius, orbital speed, and orbital energy—can be derived starting from Bohr's assumption, and they yield predictions consistent with the experimental Rydberg formula.
- While Bohr's semiclassical model of the atom does not account for all experimental facts about the atom, it is an important stepping stone to fully-quantum-mechanical models of the atom.
Glossary
- hydrogen spectrum wavelengths
- the wavelengths of visible light from hydrogen; can be calculated by \frac{1}{\lambda}=R\left(\frac{1}{n_{\mathrm{f}}^{2}}-\frac{1}{n_{\mathrm{i}}^{2}}\right)
- Rydberg constant
- a physical constant related to the atomic spectra with an established value of 1.097 \times 10^{7} \mathrm{~m}^{-1}
- double-slit interference
- an experiment in which waves or particles from a single source impinge upon two slits so that the resulting interference pattern may be observed
- energy-level diagram
- a diagram used to analyze the energy level of electrons in the orbits of an atom
- Bohr radius
- the mean radius of the orbit of an electron around the nucleus of a hydrogen atom in its ground state
- hydrogen-like atom
- any atom with only a single electron
- energies of hydrogen-like atoms
- Bohr formula for energies of electron states in hydrogen-like atoms: E_{n}=-\frac{Z^{2}}{n^{2}} E_{0}(n=1,2,3, \ldots)


