10.14: Discharge of a Capacitor through an Inductance and a Resistance
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the section and the next, the reader is assumed to have some experience in the solution of differential equations. When we arrive at a differential equation, I shall not go into the mechanics of how to solve it, I shall merely write down the solution of the equation immediately following it, without explanation. It is not assumed that a reader will immediately be able to solve the equation is his or her head, but would be able to do so given half an hour in a quiet room. Those with no experience in differential equations will have to take the solutions given on trust.
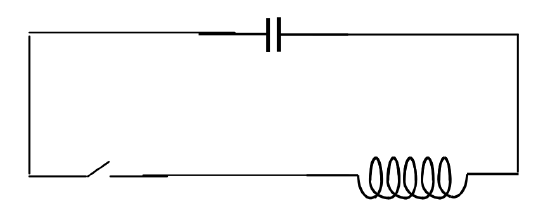
A charged capacitor of capacitance C is connected in series with a switch and an inductor of inductance L. The switch is closed, and charge flows out of the capacitor and hence a current flows through the inductor. Thus while the electric field in the capacitor diminishes, the magnetic field in the inductor grows, and a back electromotive force (EMF) is induced in the inductor. Let Q be the charge in the capacitor at some time. The current I flowing from the positive plate is equal to −˙Q. The potential difference across the capacitor is Q/C and the back EMF across the inductor is L˙I=−L¨Q. The potential drop around the whole circuit is zero, so that Q/C=−L¨Q. The charge on the capacitor is therefore governed by the differential equation
¨Q=−QLC,
which is simple harmonic motion with ω0=1/√LC. You should verify that this has dimensions T−1.
If there is a resistor of resistance R in the circuit, while a current flows through the resistor there is
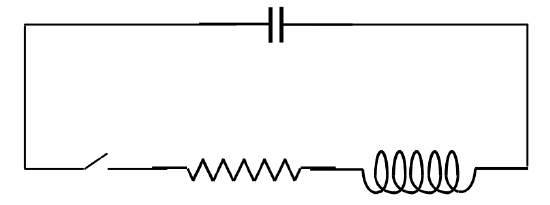
a potential drop RI=−R˙Q across it, and the differential equation governing the charge on the capacitor is then
LC¨Q+RC˙Q+Q=0.
This is damped oscillatory motion, the condition for critical damping being R2=4L/C. In fact, it is not necessary actually to have a physical resistor in the circuit. Even if the capacitor and inductor were connected by superconducting wires of zero resistance, while the charge in the circuit is slopping around between the capacitor and the inductor, it will be radiating electromagnetic energy into space and hence losing energy. The effect is just as if a resistance were in the circuit.
Those familiar with differential equations will recognize that the nature of the solution will depends on whether the resistance is greater than, less than, or equal to 2√LC. You can use the table of dimensions in Chapter 11 to verify that √LC is dimensionally similar to resistance.
If the resistance is smaller than 2√LC the charge in the capacitor will vary with time as
Q=Ke−γt/2sin(ω′t+α),
where γ=R/L and
ω′=√1LC−R24L2,
This is a sine function whose amplitude decreases exponentially with time. The constants K and α are arbitrary constants of integration, which depend upon the initial conditions. If the initial conditions are such that, at time t=0, Q=Q0 and ˙Q=I=0, then Equation ??? becomes, after a little algebra and trigonometry
Q=Q0e−γt/2(γ2ω′sinω′t+cosω′t.).
This is a sine function whose amplitude decreases exponentially with time.
If the resistance is larger than 2√LC the charge in the capacitor will vary with time as
Q=Ae−λ1t+Be−λ2t,
where
λ1=R2L−√R24L2−1LC,λ2=R2L+√R24L2−1LC
Here, and A and B are arbitrary constants of integration, which depend upon the initial conditions. If the initial conditions are such that, at time 0, Q=Q0 and ˙Q=I=0, then Equation ??? becomes
Q=Q0λ2−λ1(λ2e−λ1t−λ1e−λ2t).
Thus, with these initial conditions, Q decreases monotonically, without oscillation, to zero as t→∞.
If the resistance is equal to 2√LC the charge in the capacitor will vary with time as
Q=Ke−Rt2L(1+at).
If the initial conditions are such that, at time 0, Q=Q0 and ˙Q=I=0, then Equation ??? becomes
Q=Q0e−Rt2L(1+Rt2L),
which decreases monotonically to zero as t→∞, reaching 12Q0 at t=3.3567R/L.


