5.15: Changing the Distance Between the Plates of a Capacitor
( \newcommand{\kernel}{\mathrm{null}\,}\)
If you gradually increase the distance between the plates of a capacitor (although always keeping it sufficiently small so that the field is uniform) does the intensity of the field change or does it stay the same? If the former, does it increase or decrease?
The answers to these questions depends
- on whether, by the field, you are referring to the E-field or the D-field;
- on whether the plates are isolated or if they are connected to the poles of a battery.
We shall start by supposing that the plates are isolated.
In this case the charge on the plates is constant, and so is the charge density. Gauss’s law requires that D=σ, so that Dremains constant. And, since the permittivity hasn’t changed, E also remains constant.
The potential difference across the plates is Ed, so, as you increase the plate separation, so the potential difference across the plates in increased. The capacitance decreases from ϵA/d1 to ϵA/d2 and the energy stored in the capacitor increases from Ad1σ22ϵ to Ad2σ22ϵ. This energy derives from the work done in separating the plates.
Now let’s suppose that the plates are connected to a battery of EMF V, with air or a vacuum between the plates. At first, the separation is d1. The magnitudes of E and Dare, respectively, V/d1 and ϵ0V/d1. When we have increased the separation to d2, the potential difference across the plates has not changed; it is still the EMF V of the battery. The electric field, however, is now only E=V/d2 and D=ϵ0V/d2. But Gauss’s law still dictates that D=σ, and therefore the charge density, and the total charge on the plates, is less than it was before. It has gone into the battery. In other words, in doing work by separating the plates we have recharged the battery. The energy stored in the capacitor was originally ϵ0AV22d1; it is now only ϵ0AV22d2. Thus the energy held in the capacitor has been reduced by 12ϵ0AV2(1d1−1d2).
The charge originally held by the capacitor was ϵ0AVd1. After the plate separation has been increased to d2 the charge held is ϵ0AVd1. The difference, ϵ0AV(1d1−1d2), is the charge that has gone into the battery. The energy, or work, required to force this amount of charge into the battery against its EMF V is ϵ0AV2(1d1−1d2). Half of this came from the loss in energy held by the capacitor (see above). The other half presumably came from the mechanical work you did in separating the plates. Let’s see if we can verify this.
When the plate separation is x, the force between the plates is 12QE which is 12ϵ0AVx⋅Vx or ϵ0AV22x2. The work required to increase x from d1 to d2 is ϵ0AV22∫d2d1dxx2, which is indeed 12ϵ0AV2(1d1−1d2). Thus this amount of mechanical work, plus an equal amount of energy from the capacitor, has gone into recharging the battery. Expressed otherwise, the work done in separating the plates equals the work required to charge the battery minus the decrease in energy stored by the capacitor.
Perhaps we have invented a battery charger (Figure V.19)!
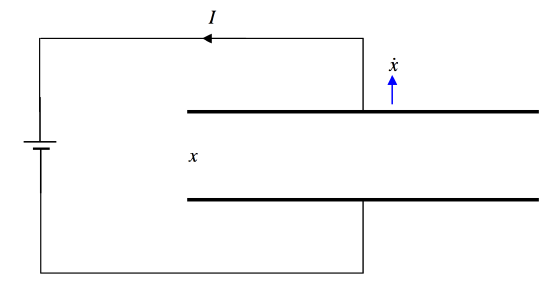
FIGURE V.19
When the plate separation is x, the charge stored in the capacitor is Q=ϵ0AVx. If x is increased at a rate ˙x, Q will increase at a rate ˙Q=−ϵ0AV˙xx2. That is, the capacitor will discharge (because ˙Q is negative), and a current I=ϵ0AV˙xx2 will flow counterclockwise in the circuit. (Verify that this expression is dimensionally correct for current.)


