5.16: Potential Field Within a Parallel Plate Capacitor
( \newcommand{\kernel}{\mathrm{null}\,}\)
This section presents a simple example that demonstrates the use of Laplace’s Equation (Section 5.15) to determine the potential field in a source free region. The example, shown in Figure 5.16.1, pertains to an important structure in electromagnetic theory – the parallel plate capacitor. Here we are concerned only with the potential field V(r) between the plates of the capacitor; you do not need to be familiar with capacitance or capacitors to follow this section (although you’re welcome to look ahead to Section 5.22 for a preview, if desired). What is recommended before beginning is a review of the battery-charged capacitor experiment discussed in Section 2.2. In this section you’ll see a rigorous derivation of what we figured out in an informal way in that section.
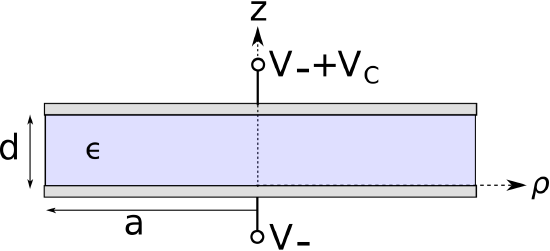 Figure 5.16.1: A parallel plate capacitor, as a demonstration of the use of Laplace's Equation.
Figure 5.16.1: A parallel plate capacitor, as a demonstration of the use of Laplace's Equation.
The parallel-plate capacitor in Figure 5.16.1 consists of two perfectly-conducting circular disks separated by a distance d by a spacer material having permittivity ϵ. There is no charge present in the spacer material, so Laplace’s Equation applies. That equation is (Section 5.15): ∇2V=0 (source-free region)
This problem has cylindrical symmetry, so it makes sense to continue to use cylindrical coordinates with the z axis being perpendicular to the plates. Equation ??? in cylindrical coordinates is:
[1ρ∂∂ρ(ρ∂∂ρ)+1ρ2∂2∂ϕ2+∂2∂z2]V=0
or perhaps a little more clearly written as follows:
1ρ∂∂ρ(ρ∂V∂ρ)+1ρ2∂2V∂ϕ2+∂2V∂z2=0
Since the problem has radial symmetry, ∂V/∂ϕ=0. Since d≪a, we expect the fields to be approximately constant with ρ until we get close to the edge of the plates. Therefore, we assume ∂V/∂ρ is negligible and can be taken to be zero. Thus, we are left with ∂2V∂z2≈0 for ρ≪a
The general solution to Equation ??? is obtained simply by integrating both sides twice, yielding
V(z)=c1z+c2
where c1 and c2 are constants that must be consistent with the boundary conditions. Thus, we must develop appropriate boundary conditions. Let the node voltage at the negative (z=0) terminal be V−. Then the voltage at the positive (z=+d) terminal is V−+VC. Therefore: These are the relevant boundary conditions. Substituting V(z=0)=V− into Equation ??? yields c2=V−. Substituting V(z=+d)=V−+VC into Equation ??? yields c1=VC/d. Thus, the answer to the problem is
V(z)≈VCdz+V− for ρ≪a
Note that the above result is dimensionally correct and confirms that the potential deep inside a “thin” parallel plate capacitor changes linearly with distance between the plates.
Further, you should find that application of the equation E=−∇V (Section 5.14) to the solution above yields the expected result for the electric field intensity: E≈−ˆzVC/d. This is precisely the result that we arrived at (without the aid of Laplace’s Equation) in Section 2.2.
A reasonable question to ask at this point would be, what about the potential field close to the edge of the plates, or, for that matter, beyond the plates? The field in this region is referred to as a fringing field. For the fringing field, ∂V/∂ρ is no longer negligible and must be taken into account. In addition, it is necessary to modify the boundary conditions to account for the outside surfaces of the plates (that is, the sides of the plates that face away from the dielectric) and to account for the effect of the boundary between the spacer material and free space. These issues make the problem much more difficult. When an accurate calculation of a fringing field is necessary, it is common to resort to a numerical solution of Laplace’s Equation. Fortunately, accurate calculation of fringing fields is usually not required in practical engineering applications.


