4.5: Exercise Problems
( \newcommand{\kernel}{\mathrm{null}\,}\)
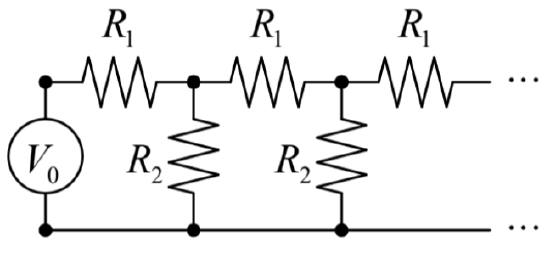
4.1. DC voltage V0 is applied to the end of a semi-infinite chain of lumped Ohmic resistors, shown in the figure on the right. Calculate the voltage across the jth link of the chain.
4.2. It is well known that properties of many dc current sources (e.g., batteries) may be reasonably well represented as a connection in series of a perfect voltage source and an Ohmic internal resistance. Discuss the option, and possible advantages, of using a different equivalent circuit that would include a perfect current source.
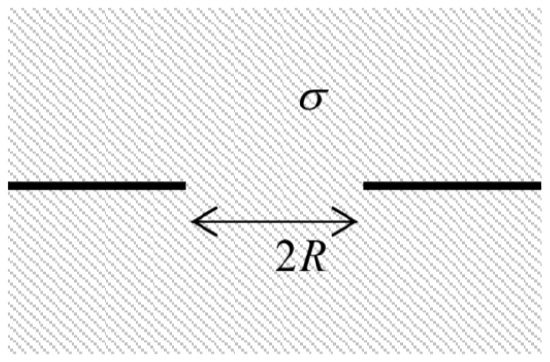
4.3. Calculate the resistance between two large, uniform Ohmic conductors separated by a very thin, plane, insulating partition, with a circular hole of radius R in it – see the figure on the right.
Hint: You may like to use the degenerate ellipsoidal coordinates, which have been discussed in Sec. 2.4.
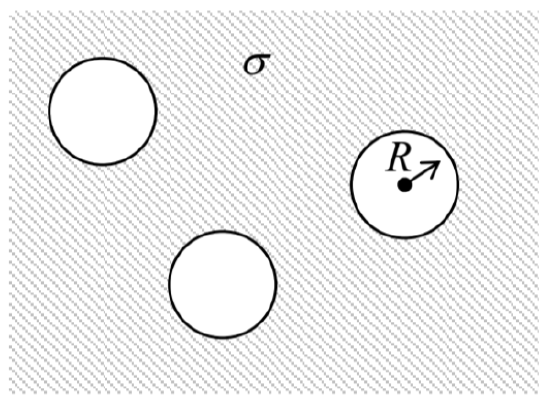
4.4. Calculate the effective (average) conductivity σef of a medium with many empty spherical cavities of radius R, carved at random positions in a uniform Ohmic conductor (see the figure on the right), in the limit of a low density n<<R−3 of the spheres.
Hint: Try to use the analogy with a dipole medium – see, e.g., Sec. 3.2.
4.5. In two separate experiments, a narrow gap, possibly of irregular width, between two close metallic electrodes is filled with some material: in the first case, with a uniform linear insulator with an electric permittivity E, and in the second case, with a uniform conducting material with an Ohmic conductivity σ. Neglecting the fringe effects, calculate the relation between the mutual capacitance C between the electrodes (in the first case) and the dc resistance R between them (in the second case).
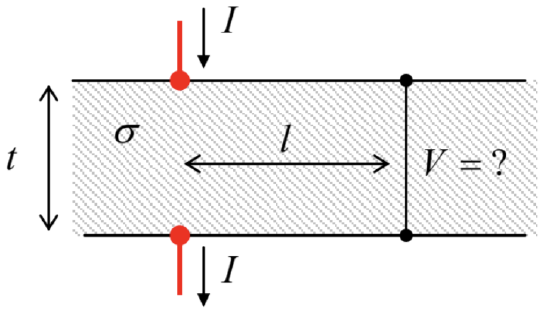
4.6. Calculate the voltage V across a uniform, wide resistive slab of thickness t, at distance l from the points of injection/pickup of the dc current I passed across the slab – see the figure on the right.
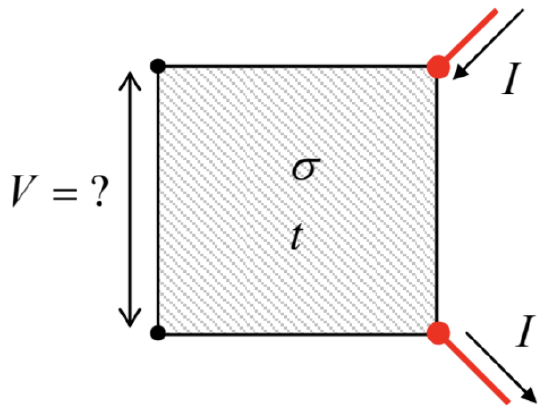
4.7. Calculate the voltage V between two corners of a square cut from a uniform, resistive sheet of a very small thickness t, induced by dc current I that is passed between its two other corners – see the figure on the right.
4.8. Calculate the distribution of the dc current’s density in a thin, round, uniform resistive disk, if the current is inserted into some point at its rim, and picked up at the center.
4.9.* The simplest reasonable model of a vacuum diode consists of two plane, parallel metallic electrodes of area A, separated by a gap of thickness d<<A1/2: a “cathode” that emits electrons into the gap, and an “anode” that absorbs the electrons arriving from the gap at its surface. Calculate the dc I−V curve of the diode, i.e. the stationary relation between the current I flowing between the electrodes and the voltage V applied between them, using the following simplifying assumptions:
(i) due to the effect of the negative space charge of the emitted electrons, the current I is much lower than the emission ability of the cathode,
(ii) the initial velocity of the emitted electrons is negligible, and
(iii) the direct Coulomb interaction of electrons (besides the space charge effect) is negligible.
4.10.* Calculate the space-charge-limited current in a system with the same geometry as in the previous problem, and using the same assumptions besides that now the emitted charge carriers move not ballistically, but drift in accordance with the Ohm law, with the conductivity given by Eq. (4.13): σ=q2μn, with a constant mobility μ.19
Hint: In order to get a realistic result, assume that the medium in that the charge carriers move has a certain dielectric constant κ unrelated to the carriers.
4.11. Prove that the distribution of dc currents in a uniform Ohmic conductor, at a fixed voltage applied at its boundaries, corresponds to the minimum of the total energy dissipation rate (“Joule heat”).
Reference
19 As was mentioned in Sec. 2, the approximation of a constant (in particular, field- and charge-density-independent) mobility is most suitable for semiconductors.


