9.1: Einstein Postulates and the Lorentz Transform

As was emphasized at the derivation of expressions for the dipole and quadrupole radiation in the last chapter, they are only valid for systems of non-relativistic particles. Thus, these results cannot be used for the description of such important phenomena as the Cherenkov radiation or the synchrotron radiation, in which relativistic effects are essential. Moreover, an analysis of the motion of charged relativistic particles in electric and magnetic fields is also a natural part of electrodynamics. This is why I will follow the tradition of using this course for a (by necessity, brief) introduction to the special relativity theory. This theory is based on the fundamental idea that measurements of physical variables (including the spatial and even temporal intervals between two events) may give different results in different reference frames, in particular in two inertial frames moving relative to each other translationally (i.e. without rotation), with a certain constant velocity v (Fig. 1).

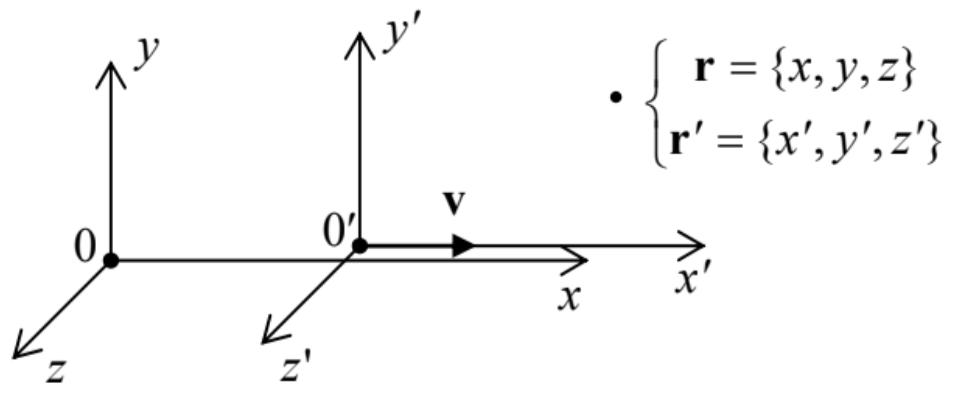Fig. 9.1. The translational, uniform mutual motion of two reference frames.

In the non-relativistic (Newtonian) mechanics the problem of transfer between such reference frames has a simple solution at least in the limit \(\ \nu<<c\), because the basic equation of particle dynamics (the 2^nd Newton law)¹

\[\ m_{k} \ddot{\mathbf{r}}_{k}=-\nabla_{k} \sum_{k^{\prime}} U\left(\mathbf{r}_{k}-\mathbf{r}_{k^{\prime}}\right),\tag{9.1}\]

where \(\ U\) is the potential energy of inter-particle interactions, is invariant with respect to the so-called Galilean transformation (or just “transform” for short).² Choosing the coordinates in both frames so that their axes x and x’ are parallel to the vector v (as in Fig. 1), the transform³ may be represented as

\[\ x=x^{\prime}+\nu t^{\prime}, \quad y=y^{\prime}, \quad z=z^{\prime}, \quad t=t^{\prime},\text{Galilean transform}\tag{9.2a}\]

and plugging Eq. (2a) into Eq. (1), we get an absolutely similarly looking equation of motion in the “moving” reference frame 0’. Since the reciprocal transform,

\[\ x^{\prime}=x-\nu t, \quad y=y^{\prime}, \quad z^{\prime}=z, \quad t^{\prime}=t,\tag{9.2b}\]

is similar to the direct one, with the replacement of \(\ (+\nu)\) with \(\ (-\nu)\), we may say that the Galilean invariance means that there is no any “master” (absolute) spatial reference frame in classical mechanics, although the spatial and temporal intervals between different instant events are absolute, i.e. reference-frame invariant: \(\ \Delta x=\Delta x^{\prime}, \ldots, \Delta t=\Delta t^{\prime}\).

However, it is straightforward to use Eq. (2) to check that the form of the wave equation

\[\ \left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}-\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}}\right) f=0,\tag{9.3}\]

Describing, in particular, the electromagnetic wave propagation in free space,⁴ is not Galilean-invariant.⁵ For the “usual” (say, elastic) waves, which obey a similar equation albeit with a different speed,⁶ this lack of Galilean invariance is natural and is compatible with the invariance of Eq. (1), from which the wave equation originates. This is because the elastic waves are essentially the oscillations of interacting particles of a certain medium (e.g., an elastic solid), which makes the reference frame connected to this medium, special. So, if the electromagnetic waves were oscillations of a certain special medium (which was first called the “luminiferous aether”⁷ and later aether – or just “ether”), similar arguments might be applicable to reconcile Eqs. (2) and (3).

The detection of such a medium was the goal of the measurements carried out between 1881 and 1887 (with better and better precision) by Albert Abraham Michelson and Edward Williams Morley, which are sometimes called “the most famous failed experiments in physics”. Figure 2 shows a crude scheme of these experiments.

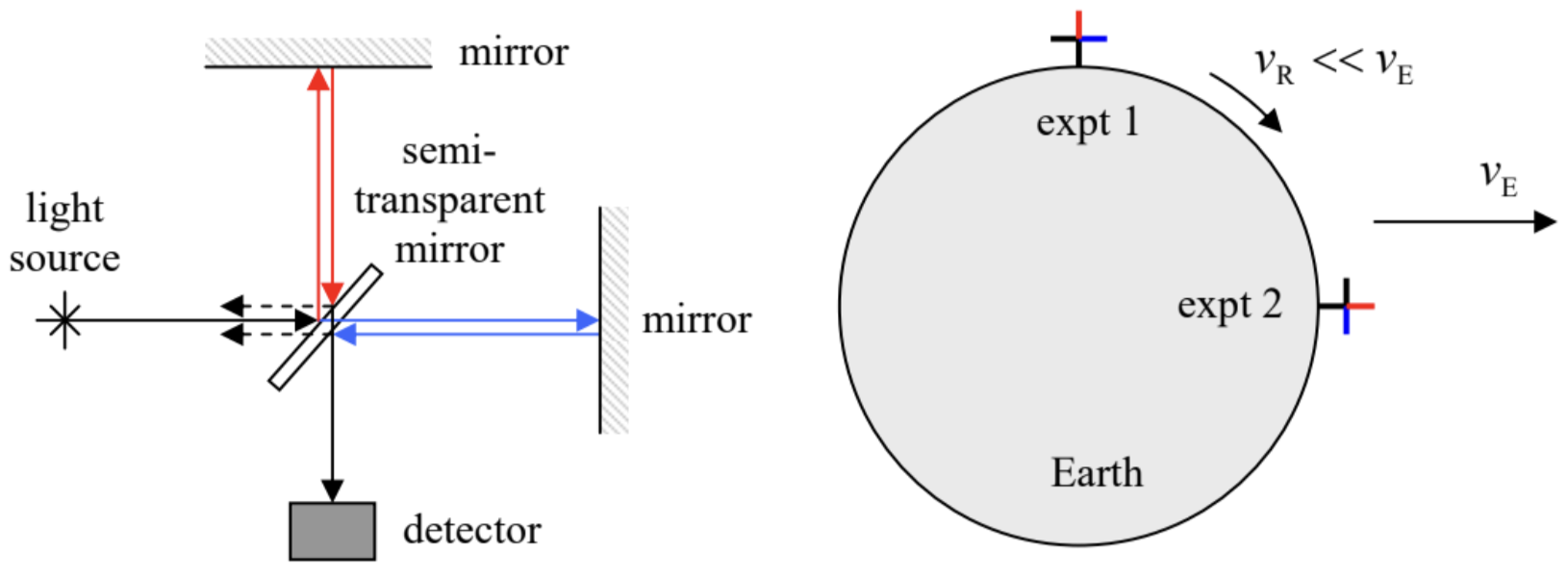Fig. 9.2. The Michelson-Morley experiment.

A nearly-monochromatic wave from a light source is split into two parts (nominally, of equal intensity), using a semi-transparent mirror tilted by \(\ \pi / 2\) to the incident wave direction. These two partial waves are reflected back by two fully-reflecting mirrors, and arrive at the same semi-transparent mirror again. Here a half of each wave is returned to the light source area (where they vanish without affecting the source), but another half is passed toward a detector, forming, with its counterpart, an interference pattern similar to that in the Young experiment. Thus each of the interfering waves has traveled twice (back and forth) each of two mutually perpendicular “arms” of the interferometer. Assuming that the aether, in which light propagates with speed \(\ c\), moves with speed \(\ \nu<c\) along one of the arms, of length \(\ l_{l}\), it is straightforward (and hence left for reader’s exercise :-) to get the following expression for the difference between the light roundtrip times:

\[\ \Delta t=\frac{2}{c}\left[\frac{l_{t}}{\left(1-\nu^{2} / c^{2}\right)^{1 / 2}}-\frac{l_{l}}{1-\nu^{2} / c^{2}}\right] \approx \frac{l}{c}\left(\frac{\nu}{c}\right)^{2},\tag{9.4}\]

where \(\ l_{t}\) is the length of the second, “transverse” arm of the interferometer (perpendicular to v), and the last, approximate expression is valid at \(\ l_{t} \approx l_{l} \equiv l\) and \(\ \nu<<c\).

Since the Earth moves around the Sun with a speed \(\ \nu_{\mathrm{E}} \approx 30 \mathrm{~km} / \mathrm{s} \approx 10^{-4} c\), the arm positions relative to this motion alternate, due to the Earth’s rotation about its axis, every 6 hours – see the right panel of Fig. 2. Hence if we assume that the aether rests in the Sun’s reference frame, \(\ \Delta t\) (and the corresponding shift of the interference fringes), has to change its sign with this half-period as well. The same alternation may be achieved, at a smaller time scale, by a deliberate rotation of the instrument by \(\ \pi / 2\). In the most precise version of the Michelson-Morley experiment (1887), this shift was expected to be close to 0.4 of the interference pattern period. The results of the search for such a shift were negative, with the error bar about 0.01 of the period.⁸

The most prominent immediate explanation of this zero result⁹ was suggested in 1889 by George Francis FitzGerald and (independently and more qualitatively) by H. Lorentz in 1892: as evident from Eq. (4), if the longitudinal arm of the interferometer itself experiences the so-called length contraction,

\[\ l_{l}(\nu)=l_{l}(0)\left(1-\frac{\nu^{2}}{c^{2}}\right)^{1 / 2},\tag{9.5}\]

while the transverse arm’s length is not affected by its motion through the aether, this kills the shift \(\ \Delta t\). This radical idea received strong support from the proof, in 1887-1905, that the Maxwell equations, and hence the wave equation (3), are form-invariant under the so-called Lorentz transform,¹⁰ which in particular describes Eq. (5). For the choice of coordinates shown in Fig. 1, the transform reads

\[\ x=\frac{x^{\prime}+\nu t^{\prime}}{\left(1-\nu^{2} / c^{2}\right)^{1 / 2}}, \quad y=y^{\prime}, \quad z=z^{\prime}, \quad t=\frac{t^{\prime}+\left(\nu / c^{2}\right) x^{\prime}}{\left(1-\nu^{2} / c^{2}\right)^{1 / 2}}.\text{Lorentz transform}\tag{9.6a}\]

It is elementary to solve these equations for the primed coordinates to get the reciprocal transform

\[\ x^{\prime}=\frac{x-\nu t}{\left(1-\nu^{2} / c^{2}\right)^{1 / 2}}, \quad y^{\prime}=y, \quad z^{\prime}=z, \quad t^{\prime}=\frac{t-\left(\nu / c^{2}\right) x}{\left(1-\nu^{2} / c^{2}\right)^{1 / 2}}.\tag{9.6b}\]

(I will soon represent Eqs. (6) in a more elegant form – see Eqs. (19) below.)

The Lorentz transform relations (6) are evidently reduced to the Galilean transform formulas (2) at \(\ \nu^{2}<< c^{2}\). However, all attempts to give a reasonable interpretation of these equalities while keeping the notion of the aether have failed, in particular because of the restrictions imposed by results of earlier experiments carried out in 1851 and 1853 by Hippolyte Fizeau – that were repeated with higher accuracy by the same Michelson and Morley in 1886. These experiments have shown that if one sticks to the aether concept, this hypothetical medium has to be partially “dragged” by any moving dielectric material with a speed proportional to (\(\ \kappa-1\)). Such local drag would be irreconcilable with the assumed continuity of the aether.

In his famous 1905 paper, Albert Einstein has suggested a bold resolution of this contradiction, essentially removing the concept of the aether altogether.¹¹ Moreover, he argued that the Lorentz transform is the general property of time and space, rather than of the electromagnetic field alone. He has started with two postulates, the first one essentially repeating the principle of relativity, formulated earlier (1904) by H. Poincaré in the following form:

“...the laws of physical phenomena should be the same, whether for an observer fixed or for an observer carried along in a uniform movement of translation; so that we have not and could not have any means of discerning whether or not we are carried along in such a motion.”¹²

The second Einstein’s postulate was that the speed of light \(\ c\), in free space, should be constant in all reference frames. (This is essentially a denial of the aether’s existence.)

Then, Einstein showed that the Lorenz transform relations (6) naturally follow from his postulates, with a few (very natural) additional assumptions. Let a point source emit a short flash of light, at the moment \(\ t=t^{\prime}=0\) when the origins of the reference frames shown in Fig. 1 coincide. Then, according to the second of Einstein’s postulates, in each of the frames, the spherical wave propagates with the same speed \(\ c\), i.e. the coordinates of points of its front, measured in the two frames, have to obey the following equalities:

\[\ \begin{aligned}
&(c t)^{2}-\left(x^{2}+y^{2}+z^{2}\right)=0, \\
&\left(c t^{\prime}\right)^{2}-\left(x^{\prime 2}+y^{\prime 2}+z^{\prime 2}\right)=0.
\end{aligned}\tag{9.7}\]

What may be the general relation between the combinations in the left-hand side of these equations – not for this particular wave’s front, but in general? A very natural (essentially, the only justifiable) choice is

\[\ \left[(c t)^{2}-\left(x^{2}+y^{2}+z^{2}\right)\right]=f\left(\nu^{2}\right)\left[\left(c t^{\prime}\right)^{2}-\left(x^{\prime 2}+y^{\prime 2}+z^{\prime 2}\right)\right].\tag{9.8}\]

Now, according to the first postulate, the same relation should be valid if we swap the reference frames (\(\ x \leftrightarrow x^{\prime}\), etc.) and replace \(\ \nu\) with \(\ (-\nu)\). This is only possible if \(\ f^{2}=1\), so that excluding the option \(\ f=-1\) (which is incompatible with the Galilean transform in the limit \(\ \nu / c \rightarrow 0\)), we get

\[\ (c t)^{2}-\left(x^{2}+y^{2}+z^{2}\right)=\left(c t^{\prime}\right)^{2}-\left(x^{\prime 2}+y^{\prime 2}+z^{\prime 2}\right).\tag{9.9}\]

For the line with \(\ y=y^{\prime}=0\), \(\ z=z^{\prime}=0\), Eq. (9) is reduced to

\[\ (c t)^{2}-x^{2}=\left(c t^{\prime}\right)^{2}-x^{\prime 2}.\tag{9.10}\]

It is very illuminating to interpret this relation as the one resulting from a mutual rotation of the reference frames (that now have to include clocks to measure time) on the plane of the coordinate \(\ x\) and the so-called Euclidian time \(\ \tau \equiv i c t\) – see Fig. 3.

Fig. 9.3. The Lorentz transform as a mutual rotation of two reference frames on the \(\ [x, \tau]\) plane.

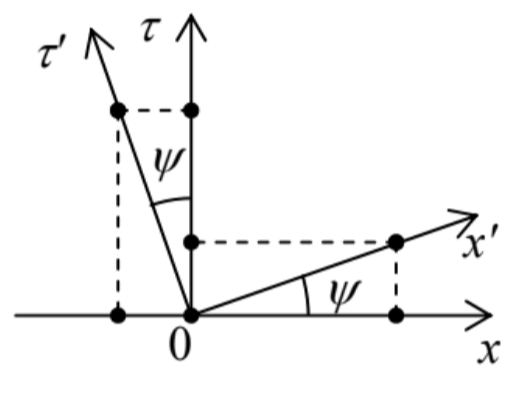
Indeed, rewriting Eq. (10) as

\[\ \tau^{2}+x^{2}=\tau^{\prime 2}+x^{\prime 2},\tag{9.11}\]

we may consider it as the invariance of the squared radius at the rotation that is shown in Fig. 3 and described by the following geometric relations:

\[\ \begin{aligned}
&x=x^{\prime} \cos \psi-\tau^{\prime} \sin \psi, \\
&\tau=x^{\prime} \sin \psi+\tau^{\prime} \cos \psi,
\end{aligned}\tag{9.12a}\]

with the reciprocal relations

\[\ \begin{aligned}
&x^{\prime}=x \cos \psi+\tau \sin \psi, \\
&\tau^{\prime}=-x \sin \psi+\tau \cos \psi.
\end{aligned}\tag{9.12b}\]

So far, the angle \(\ \psi\) has been arbitrary. In the spirit of Eq. (8), a natural choice is \(\ \psi=\psi(\nu)\), with the requirement \(\ \psi(0)=0\). To find this function, let us write the definition of the velocity \(\ \nu\) of the frame 0’, as measured in the frame 0 (which was implied above): for \(\ x^{\prime}=0, x=\nu t\). In the variables \(\ x\) and \(\ \mathcal{\tau}\), this means

\[\ \left.\left.\frac{x}{\tau}\right|_{x^{\prime}=0} \equiv \frac{x}{i c t}\right|_{x^{\prime}=0}=\frac{\nu}{i c}.\tag{9.13}\]

On the other hand, for the same point \(\ x^{\prime}=0\), Eqs. (12a) yield

\[\ \left.\frac{x}{\tau}\right|_{x^{\prime}=0}=-\tan \psi.\tag{9.14}\]

These two expressions are compatible only if

\[\ \tan \psi=i \nu / c,\tag{9.15}\]

so that

\[\ \sin \psi \equiv \frac{\tan \psi}{\left(1+\tan ^{2} \psi\right)^{1 / 2}}=\frac{i \nu / c}{\left(1-\nu^{2} / c^{2}\right)^{1 / 2}} \equiv i \beta \gamma, \quad \cos \psi \equiv \frac{1}{\left(1+\tan ^{2} \psi\right)^{1 / 2}}=\frac{1}{\left(1-\nu^{2} / c^{2}\right)^{1 / 2}} \equiv \gamma,\tag{9.16}\]

where \(\ \beta\) and \(\ \gamma\) are two very convenient and commonly used dimensionless parameters defined as

\[\ \boldsymbol{\beta} \equiv \frac{\mathbf{v}}{c}, \quad \gamma \equiv \frac{1}{\left(1-\nu^{2} / c^{2}\right)^{1 / 2}} \equiv \frac{1}{\left(1-\beta^{2}\right)^{1 / 2}}.\quad\quad\quad\quad\text{Relativistic parameters }\beta \text{ and } \gamma\tag{9.17}\]

(The vector \(\ \beta\) is called normalized velocity, while the scalar \(\ \gamma\), the Lorentz factor.)¹³

Using the relations for \(\ \psi\), Eqs. (12) become

\[\ x=\gamma\left(x^{\prime}-i \beta \tau^{\prime}\right), \quad \tau=\gamma\left(i \beta x^{\prime}+\tau^{\prime}\right),\tag{9.18a}\]

\[\ x^{\prime}=\gamma(x+i \beta \tau), \quad \tau^{\prime}=\gamma(-i \beta x+\tau).\tag{9.18b}\]

Now returning to the real variables \(\ [x, c t]\), we get the Lorentz transform relations (6), in a more compact form:

\[\ x=\gamma\left(x^{\prime}+\beta c t^{\prime}\right), \quad y=y^{\prime}, \quad z=z^{\prime}, \quad c t=\gamma\left(c t^{\prime}+\beta x^{\prime}\right),\tag{9.19a}\]

Lorentz transform - again

\[\ x^{\prime}=\gamma(x-\beta c t), \quad y^{\prime}=y, \quad z^{\prime}=z, \quad c t^{\prime}=\gamma(c t-\beta x).\tag{9.19b}\]

An immediate corollary of Eqs. (19) is that for \(\ \gamma\) to stay real, we need \(\ \nu^{2} \leq c^{2}\), i.e. that the speed of any physical body (to which we could connect a meaningful reference frame) cannot exceed the speed of light, as measured in any other meaningful reference frame.¹⁴

---

Reference

¹ Let me hope that the reader does not need a reminder that for Eq. (1) to be valid, the reference frames 0 and 0’ have to be inertial – see, e.g., CM Sec. 1.2.

² It had been first formulated by Galileo Galilei, if only rather informally, as early as in 1638 – four years before Isaac Newton was born!

³ Note the very unfortunate term “boost”, used sometimes to describe such transform. (It is especially unnatural in the special relativity, not describing accelerating reference frames.) In my course, this term is avoided.

⁴ The discussions in this chapter and most of the next chapter will be restricted to the free-space (and hence dispersion-free) case; some media effects on the radiation by relativistic particles will be discussed in Sec.10.4.

⁵ It is interesting that the usual Schrödinger equation, whose fundamental solution for a free particle is a similar monochromatic wave (albeit with a different dispersion law), is Galilean-invariant, with a certain addition to the wavefunction’s phase – see, e.g., QM Chapter 1. This is natural because that equation is non-relativistic.

⁶ See, e.g., CM Secs. 6.5 and 7.7.

⁷ In ancient Greek mythology, aether is the clean air breathed by the gods residing on Mount Olympus.

⁸ Through the 20^th century, the Michelson-Morley-type experiments were repeated using more and more refined experimental techniques, always with zero results for the apparent aether motion speed. For example, recent experiments using cryogenically cooled optical resonators, have reduced the upper limit for such speed to just \(\ 3 \times 10^{-15} c\) –see H. Müller et al., Phys. Rev. Lett. 91, 020401 (2003).

⁹ The zero result of a slightly later experiment, namely precise measurements of the torque which should be exerted by the moving aether on a charged capacitor, carried out in 1903 by F. Trouton and H. Noble (following G. FitzGerald’s suggestion), seconded the Michelson and Morley’s conclusions.

¹⁰ The theoretical work toward this goal included important contributions by Woldemart Voigt (in 1887), Hendrik Lorentz (in 1892-1904), Joseph Larmor (in 1897 and 1900), and Henri Poincaré (in 1900 and 1905).

¹¹ In hindsight, this was much relief, because the aether had been a very awkward construct to start with. In particular, according to the basic theory of elasticity (see, e.g., CM Ch. 7), in order to carry such transverse waves as the electromagnetic ones, this medium would need to have a non-zero shear modulus, i.e. behave as an elastic solid – rather than as a rarified gas hypothesized initially by C. Huygens.

¹² Note that though the relativity principle excludes the notion of the special (“absolute”) spatial reference frame, its verbal formulation still leaves the possibility of the Galilean “absolute time” \(\ t=t^{\prime}\) open. The quantitative relativity theory kills this option – see Eqs. (6) and their discussion below.

¹³ Note the following identities: \(\ \gamma^{2} \equiv 1 /\left(1-\beta^{2}\right)\) and \(\ \left(\gamma^{2}-1\right) \equiv \beta^{2} /\left(1-\beta^{2}\right) \equiv \gamma^{2} \beta^{2}\), which are frequently handy for the relativity-related algebra. One more function of \(\ \beta\), the rapidity \(\ \varphi \equiv \tanh ^{-1} \beta\) (so that \(\ \psi=i \varphi\)), is also useful for some calculations.

¹⁴ All attempts to rationally conjecture particles moving with \(\ \nu>c\), called tachyons, have failed – so far, at least. Possibly the strongest objection against their existence is the fact that the tachyons could be used to communicate back in time, thus violating the causality principle – see, e.g., G. Benford et al., Phys. Rev. D 2, 263 (1970).