9.9: Exercise Problems

9.1. Use the pre-relativistic picture of the Doppler effect, in which light propagates with velocity \(\ c\) in a Sun-bound aether, to derive Eq. (4).

9.2. Show that two successive Lorentz space/time transforms in the same direction, with velocities \(\ u^{\prime}\) and \(\ \nu\), are equivalent to a single transform with the velocity \(\ u\) given by Eq. (25).

9.3. \(\ N+1\) reference frames, numbered by index \(\ n\) (taking values \(\ 0,1, \ldots, N\)), move in the same direction as a particle. Express the particle’s velocity in the frame number 0 via its velocity \(\ u_{N}\) in the frame number \(\ N\), and the set of velocities \(\ \nu_{n}\) of the frame number \(\ n\) relative to the frame number \(\ (n – 1)\).

9.4. A spaceship moving with a constant velocity v directly from the Earth, sends back brief flashes of light with a period \(\ \Delta t_{s}\)– as measured by the spaceship's clock. Calculate the period with which Earth's observers receive the signals – as measured by the Earth's clock.

9.5. From the point of view of observers in a “moving” reference frame 0', a straight thin rod, parallel to the x'-axis, is moving without rotation with a constant velocity u' directed along the y'-axis. The reference frame 0' is itself moving relative to another ("lab") reference frame 0 with a constant

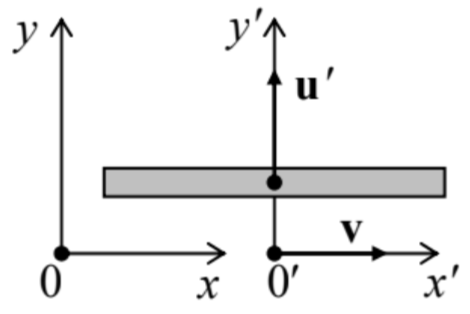
velocity v along the x-axis, also without rotation – see the figure above. Calculate:

(i) the direction of the rod's velocity, and

(ii) the orientation of the rod on the [x, y] plane,

both as observed from the lab reference frame. Is the velocity, in this frame, perpendicular to the rod?

9.6. Starting from the rest at \(\ t = 0\), a spaceship moves directly from the Earth, with a constant acceleration as measured in its instantaneous rest frame. Find its displacement \(\ x(t)\) from the Earth, as measured from Earth’s reference frame, and interpret the result.

Hint: The instantaneous rest frame of a moving particle is the inertial reference frame that, at the considered moment of time, has the same velocity as the particle.

9.7. Calculate the first relativistic correction to the frequency of a harmonic oscillator as a function of its amplitude.

9.8. An atom, with an initial rest mass m, has been excited to an internal state with an additional energy \(\ \Delta \mathscr{E}\), still being at rest. Next, it returns into its initial state, emitting a photon. Calculate the photon’s frequency, taking into account the relativistic recoil of the atom.

Hint: In this problem, and in Problems 11-13, treat photons as ultra-relativistic point particles with zero rest mass, energy \(\ \mathscr{E}=\hbar \omega\), and momentum \(\ \mathbf{p}=\hbar \mathbf{k}\).

9.9. A particle of mass \(\ m\), initially at rest, decays into two particles, with rest masses \(\ m_{1}\) and \(\ m_{2}\). Calculate the total energy of the first decay product, in the reference frame moving with that particle.

9.10. A relativistic particle with a rest mass \(\ m\), moving with velocity \(\ u\), decays into two particles with zero rest mass.

(i) Calculate the smallest possible angle between the decay product velocities (in the lab frame, in that the velocity \(\ u\) is measured).

(ii) What is the largest possible energy of one product particle?

9.11. A relativistic particle propagating with velocity u, in the absence of external fields, decays into two photons.⁸² Calculate the angular dependence of the probability of photon detection, as measured in the lab frame.

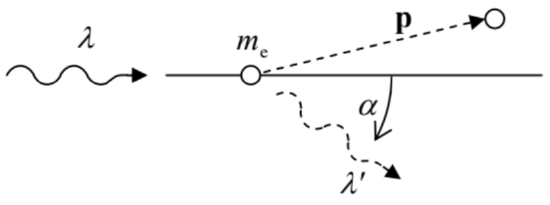
9.12. A photon with wavelength \(\ \lambda\) is scattered by an electron, initially at rest. Calculate the wavelength \(\ \lambda^{\prime}\) of the scattered photon as a function of the scattering angle \(\ \alpha\) – see the figure on the right.⁸³

9.13. Calculate the threshold energy of a \(\ \gamma\)-photon for the reaction

\(\ \gamma+\mathrm{p} \rightarrow \mathrm{p}+\pi^{0},\)

if the proton was initially at rest.

Hint: For protons \(\ m_{\mathrm{p}} c^{2} \approx 938 \mathrm{MeV}\), while for neutral pions \(\ m_{\pi} c^{2} \approx 135 \mathrm{MeV}\).

9.14. A relativistic particle with energy \(\ \mathscr{E}\) and rest mass \(\ m\), collides with a similar particle, initially at rest in the laboratory reference frame. Calculate:

(i) the final velocity of the center of mass of the system, in the lab frame,

(ii) the total energy of the system, in the center-of-mass frame, and

(iii) the final velocities of both particles (in the lab frame), if they move along the same direction.

9.15. A “primed” reference frame moves, with the reduced velocity \(\ \boldsymbol{\beta} \equiv \mathbf{v} / c=\mathbf{n}_{x} \beta\), relative to the “lab” frame. Use Eq. (109) to express the components \(\ T^{, 00}\) and \(\ T^{, 0 j}\) (with \(\ j=1,2,3\)) of an arbitrary contravariant 4-tensor \(\ T^{\gamma \delta}\) via its components in the lab frame.

9.16. Static fields E and B are uniform but arbitrary (both in magnitude and in direction). What should be the velocity of an inertial reference frame to have the vectors E’ and B’, observed from that frame, parallel? Is this solution unique?

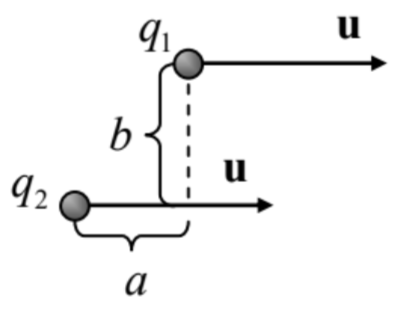
9.17. Two charged particles, moving with equal constant velocities u, are offset by distance \(\ \mathbf{R}=\{a, b\}\) (see the figure on the right), as measured in the lab
frame. Calculate the forces between the particles – also in the lab frame.

9.18. Each of two thin, long, parallel particle beams of the same velocity u, separated by distance \(\ d\), carries electric charge with a constant density \(\ \lambda\) per unit length, as measured in the reference frame moving with the particles.

(i) Calculate the distribution of the electric and magnetic fields in the system (outside the beams), as measured in the lab reference frame.

(ii) Calculate the interaction force between the beams (per particle) and the resulting acceleration, both in the lab reference frame and in the frame moving with the electrons. Compare the results and give a brief discussion of the comparison.

9.19. Spell out the Lorentz transform of the scalar-potential and vector-potential components, and use the result to calculate the potentials of a point charge \(\ q\), moving with a constant velocity u, as measured in the lab reference frame.

9.20. Calculate the scalar and vector potentials created by a time-independent electric dipole p, as measured in a reference frame that moves relative to the dipole with a constant velocity v, with the shortest distance (“impact parameter”) equal to \(\ b\).

9.21. Solve the previous problem, in the limit \(\ \nu<<c\), for a time-independent magnetic dipole m.

9.22. Assuming that the magnetic monopole does exist and has magnetic charge \(\ g\), calculate the change \(\ \Delta \Phi\) of the magnetic flux in a superconductor ring due to the passage of a single monopole through it. Evaluate \(\ \Delta \Phi\) for the monopole charge conjectured by P. Dirac, \(\ g=n g_{0} \equiv n(2 \pi \hbar / e)\), where \(\ n\) is an integer; compare the result with the magnetic flux quantum \(\ \Phi_{0}\) (6.62) with \(\ |q|=e\), and discuss their relationship.

Hint: For simplicity, you may consider monopole’s passage along the symmetry axis of a thin, round superconducting ring, in the otherwise free space.

9.23.* Calculate the trajectory of a relativistic particle in a uniform electrostatic field E, for an arbitrary direction of its initial velocity \(\ \mathbf{u}(0)\), using two different approaches – at least one of them different from the approach used in Sec. 6 for the case \(\ \mathbf{u}(0) \perp \mathbf{E}\).

9.24. A charged relativistic particle with velocity \(\ u\) performs planar cyclotron rotation in a uniform external magnetic field \(\ B\). How much would the velocity and the orbit’s radius change at a slow change of the field to a new magnitude \(\ B^{\prime}\)?

9.25.* Analyze the motion of a relativistic particle in uniform, mutually perpendicular fields E and B, for the particular case when \(\ E\) is exactly equal to \(\ cB\).

9.26.* Find the law of motion of a relativistic particle in uniform, parallel, static fields E and B.

9.27. Neglecting relativistic kinetic effects, calculate the smallest voltage \(\ V\) that has to be applied between the anode and cathode of a magnetron (see Fig. 13 and its discussion) to enable electrons to reach the anode, at negligible electron-electron interactions (including the space-charge effects), and collisions with the residual gas molecules. You may:

(i) model the cathode and anode as two coaxial round cylinders, of radii \(\ R_{1}\) and \(\ R_{2}\), respectively;

(ii) assume that the magnetic field B is uniform and directed along their common axis; and

(iii) neglect the initial velocity of the electrons emitted by the cathode.

(After the solution, estimate the validity of the last assumption, and of the non-relativistic approximation, for reasonable values of parameters.)

9.28. A charged relativistic particle has been injected into a uniform electric field whose magnitude oscillates in time with frequency \(\ \omega\). Calculate the time dependence of the particle’s velocity, as observed from the lab reference frame.

9.29. Analyze the motion of a non-relativistic particle in a region where the electric and magnetic fields are both uniform and constant in time, but not necessarily parallel or perpendicular to each other.

9.30. A static distribution of electric charge in otherwise free space has created a time-independent distribution \(\ \mathbf{E}(\mathbf{r})\) of the electric field. Use two different approaches to express the field energy density \(\ u^{\prime}\) and the Poynting vector \(\ \mathbf{S}^{\prime}\), as observed from a reference frame moving with constant velocity v, via the components of the vector E. In particular, is \(\ \mathbf{S}^{\prime}\) equal to \(\ \left(-\mathbf{v} u^{\prime}\right)\)?

9.31. A plane wave, of frequency \(\ \omega\) and intensity \(\ S\), is normally incident on a perfect mirror, moving with velocity v in the same direction as the wave.

(i) Calculate the reflected wave’s frequency, and

(ii) use the Lorentz transform of the fields to calculate the reflected wave’s intensity - both as observed from the lab reference frame.

9.32. Carry out the second task of the previous problem by using general relations between the wave’s energy, power, and momentum.

Hint: As a byproduct, this approach should also give you the pressure exerted by the wave on the moving mirror.

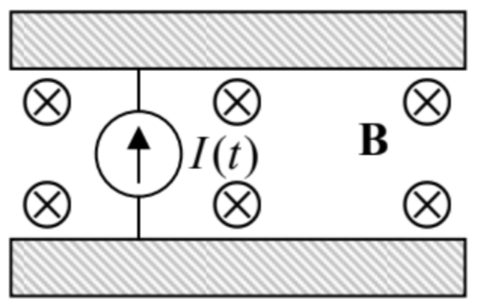
9.33. Consider the simple model of plane capacitor charging by a lumped current source, shown in the figure on the right, and prove that the momentum given by the constant, uniform external magnetic field B to the current-carrying conductor is equal and opposite to the momentum of the electromagnetic field that the current \(\ I(t)\) builds up in the capacitor. (You may assume that the capacitor is plane and very broad, and neglect the fringe field effects.)

9.34. Consider an electromagnetic plane wave packet propagating in free space, with its electric field represented as the Fourier integral

\(\ \mathbf{E}(\mathbf{r}, t)=\operatorname{Re} \int_{-\infty}^{+\infty} \mathbf{E}_{k} e^{i \psi_{k}} d k, \quad \text { with } \psi_{k} \equiv k z-\omega_{k} t, \quad \text { and } \omega_{k} \equiv c|k|.\)

Express the full linear momentum (per unit area of wave’s front) of the packet via the complex amplitudes \(\ \mathbf{E}_{k}\) of its Fourier components. Does the momentum depend on time? (In contrast with Problem 7.7, in this case the wave packet is not necessarily narrow.)

9.35. Calculate the force exerted on well-conducting walls of a waveguide with a rectangular \(\ (a \times b)\) cross-section, by a wave propagating along it in the fundamental \(\ \left(H_{10}\right)\) mode. Give an interpretation of the result.

---

Reference

⁸² Such a decay may happen, for example, with a neutral pion.

⁸³ This the famous Compton scattering effect, whose discovery in 1923 was one of the major motivations for the development of quantum mechanics – see, e.g., QM Sec. 1.1.