1.7: Continuity

Continuity

Continuity is an important concept in the theory of real functions. A continuous function is one whose output $f(x)$ does not undergo abrupt jumps when $x$ changes by tiny amounts. A function can be continuous over its entire domain, or only a subset of its domain. For example, $\sin(x)$ is continuous for all $x$, whereas $f(x) = 1/x$ is discontinuous at $x = 0$. Another function that is discontinuous at $x=0$ is the step function $$\Theta(x) = \left\{\begin{array}{ll} 1, &\;\;\;\textrm{for} \; x \ge 0\\ 0,&\;\;\; \textrm{otherwise.}\end{array}\right.$$ Mathematicians have even come up with functions that are discontinuous everywhere in their domain, but we won’t be dealing with such cases.

The rigorous definition of continuity is as follows:

Definition: Word

A function $f$ is continuous at a point $x_0$ if, for any $\epsilon >0$, we can find a $\delta >0$ such that setting $x$ closer to $x_0$ than a distance of $\delta$ brings $f(x)$ closer to $f(x_0)$ than the specified distance $\epsilon$.

That’s a very complicated sentence, and it may be easier to understand using this illustration:

Figure $\PageIndex{1}$

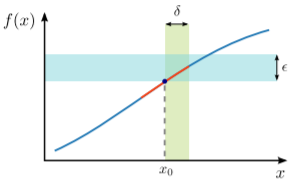
A counter-example, with a function that has a discontinuity at some $x_0$, is shown below:

Figure $\PageIndex{2}$

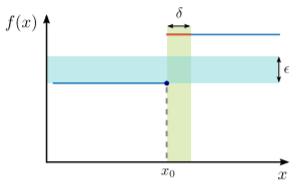
If we choose $\epsilon$ smaller than the gap, then no matter what value of $\delta > 0$ we try, any choice of $0 < x < \delta$ will give a value of $f(x)$ that’s further than $\epsilon$ from $f(x_0)$. Hence, the continuity condition is violated for sufficiently small choices of $\epsilon = 1/2$, and we say that $f$ is discontinuous at $x_0$.