2.6: Gaussian Geometrical Optics

We have seen above that by using lenses or mirrors which have surfaces that are conic sections we can perfectly image a certain pair of points, but for other points the image is in general not perfect. The imperfections are caused by rays that make larger angles with the optical axis, i.e. with the symmetry axis of the system. Rays for which these angles are small are called paraxial rays. Because for paraxial rays the angles of incidence and transmission at the surfaces of the lenses are small, the sine of the angles in Snell’s Law are replaced by the angles themselves:

\[n_{i}θ_{i}=n_{t}θ_{t}. \tag{paraxial space rays space only} \]

This approximation greatly simplifies the calculations. When only paraxial rays are considered, one may replace any refracting surface by a sphere with the same curvature at its vertex. For paraxial rays, errors caused by replacing the general surface by a sphere are of second order and hence insignificant. Spherical surfaces are not only more simple in the derivations but they are also much easier to manufacture. Hence in the optical industry spherical surfaces are used a lot. To reduce imaging errors caused by non-paraxial rays one applies two strategies:

1. adding more spherical surfaces
2. replacing one of the spherical surfaces (typically the last before image space) by a non-sphere.

In Gaussian geometrical optics only paraxial rays and spherical surfaces are considered. In Gaussian geometrical optics every point has a perfect image.

2.5.1 Gaussian Imaging by a Single Spherical Surface

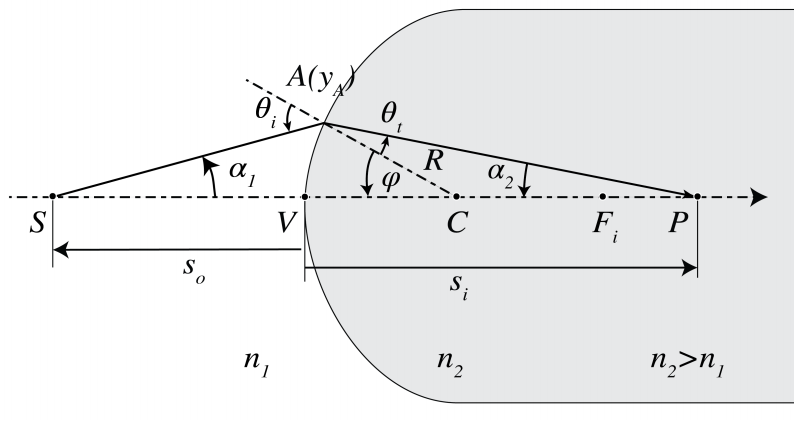
We will first show that within Gaussian optics a single spherical surface between two media with refractive indices n₁ < n₂ images all points perfectly (Figure \(\PageIndex{1}\)). The sphere has radius R and centre C which is inside medium 2. We consider a point object S to the left of the surface. We draw a ray from S perpendicular to the surface. The point of intersection is V. Since for this ray the angle of incidence with the local normal on the surface vanishes, the ray continues into the second medium without refraction and passes through the centre C of the sphere. Next we draw a ray that hits the spherical surface in some point A and draw the refracted ray in medium 2 using Snell’s law in the paraxial form (\(\PageIndex{1}\)) (note that the angles of incidence and transmission must be measured with respect to the local normal at A, i.e. with respect to CA). We assume that this ray intersects the first ray in point P. We will show that within the approximation of Gaussian geometrical optics, all rays from S pass through P. Furthermore, with respect to a coordinate system (y, z) with origin at V , the z-axis pointing from V to C and the y-axis positive upwards as shown in Figure \(\PageIndex{1}\), we have:

\[-\dfrac{n_{1}}{s_{0}}+\dfrac{n_{2}}{s_{i}}=\dfrac{n_{2}-n_{1}}{R}. \nonumber \]

where s₀ and s_i are the z-coordinates of S and P, respectively (hence s₀ < 0 and si > 0 in Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): Imaging by a spherical interface between two media with refractive indices n₂ > n₁.

Proof.

(Note: the proof is not part of the exam). It suffices to show that P is independent of the ray, i.e. of A. We will do this by expressing s_i into s_o and showing that the result is independent of A. Let α₁ and α₂ be the angles of the rays SA and AP with the z-axis as shown in Figure \(\PageIndex{1}\). Let θ_i be the angle of incidence of ray SA with the local normal CA on the surface and θ_t be the angle of refraction. By considering the angles in ∆ SCA we find

\[θ_{i}=α_{1}+ϕ. \nonumber \]

Similarly, from ∆ CPA we find

\[θ_{t}=-α_{2}+ϕ. \nonumber \]

By substitution into the paraxial version of Snell’s Law (\(\PageIndex{1}\)), we obtain

\[n_{1}α_{1}+n_{2}α_{2}=(n_{2}-n_{1})ϕ. \nonumber \]

Let y_A and z_A be the coordinates of point A. Since s_o < 0 and s_i > 0 we have

\[α_{1}≈tan(α_{1})=\dfrac{y_{A}}{z_{A}-s_{o}},α_{2}≈tan(α_{2})=\dfrac{y_{A}}{s_{i}-z_{A}}. \nonumber \]

Furthermore,

\[ϕ≈\sin ϕ≈\dfrac{y_{A}}{R}. \nonumber \]

which is small for paraxial rays. Hence,

\[z_{A}=R-R\cos ϕ=R-R(1-\dfrac{ϕ^2}{2})=\dfrac{R}{2}ϕ^2≈0, \nonumber \]

because it is second order in y_A and therefore is neglected in the paraxial approximation. Then, (\(\PageIndex{6}\) becomes

\[α_{1}=-\dfrac{y_{A}}{s_{o}},α_{2}=\dfrac{y_{A}}{s_{i}}. \nonumber \]

By substituting (\(\PageIndex{9}\) and (\(\PageIndex{7}\) into (\(\PageIndex{5}\) we find −(n₁/s_o)y_A + (n₂/z_i)y_A = [(n₂ − n₁)/R]y_A, or −n₁/s_o+n₂/z_i=(n₂ − n₁)/R,which is Eq. (\(\PageIndex{2}\). It implies that \(s_i\), and hence \(P\), is independent of y_A, i.e. of the ray chosen. Therefore, P is a perfect image within the approximation of Gaussian geometrical optics.

When s_i → ∞, the ray after refraction is parallel to the z-axis and we get so → −n₁R/(n₂ − n₁). The object point for which the rays in the medium 2 are parallel to the z-axis is called the first focal point or object focal point F_o, Its z-coordinate is:

\[f_{o}=- \dfrac{ n_{1}R }{ n_{2} -n_{1} }. \nonumber \]

In spite of the fact that this is a coordinate and hence has a sign, it is also called the front focal length or object focal length.

When s_o → −∞, the incident ray is parallel to the z-axis in medium 1 and the corresponding image point F_i is called the second focal point or image focal point. Its z-coordinate is given by:

\[f_{i}=\dfrac{ n_{2}R }{ n_{2} -n_{1} }, \nonumber \]

and it is also referred to as the second focal length or image focal length. With (\(\PageIndex{11}\)) and (\(\PageIndex{10}\)), (\(\PageIndex{2}\)) can be rewritten as:

\[- \dfrac{ n_{1}}{ s_{o} }+ \dfrac{ n_{2}}{ s_{i} } = \dfrac{ n_{2}}{ f_{i} } = -\dfrac{ n_{1}}{ f_{o} }. \nonumber \]

By adopting the sign convention listed in Table \(\PageIndex{1}\) below, it turns out that (\(\PageIndex{2}\)) holds generally. For example, when point S is between the front focal point and the vertex V so that f_o < s_o < 0, the rays from S are so strongly diverging that the refraction is insufficient to obtain an image point in medium 2. Instead there is a diverging ray bundle in medium 2 which for an observer in medium 2 seems to come from a point P in medium 1 with z-coordinate si , hence si < 0, in agreement with the fact that P is now to the left of V. Point P is called a virtual image because it does not correspond to an actual concentration of light energy in space. When s_i > 0 there is a concentration of light energy in P which therefore is then called a real image.

Figure \(\PageIndex{2}\): Imaging of a virtual object S by a spherical interface between two media with refractive indices n₁ > n₂.

Table \(\PageIndex{1}\): Sign convention for spherical surfaces and thin lenses. The convention for s_o, f_o, s_i, f_i follows from the fact that these are z-coordinates with the origin at vertex V and the positive z-axis pointing to the right.

quantity	positive	negative
so, fo, si, fi	corresponding point is to the right of vertex	corresponding point is to left of vertex
R	centre of curvature right of vertex	centre of curvature left of vertex
α (astute ray angle)	if counter clockwise rotation over α makes ray parallel to z-axis	if clockwise rotation over α makes ray parallel to z-axis
Refr. index n ambient medium of mirror	before reflection	after reflection

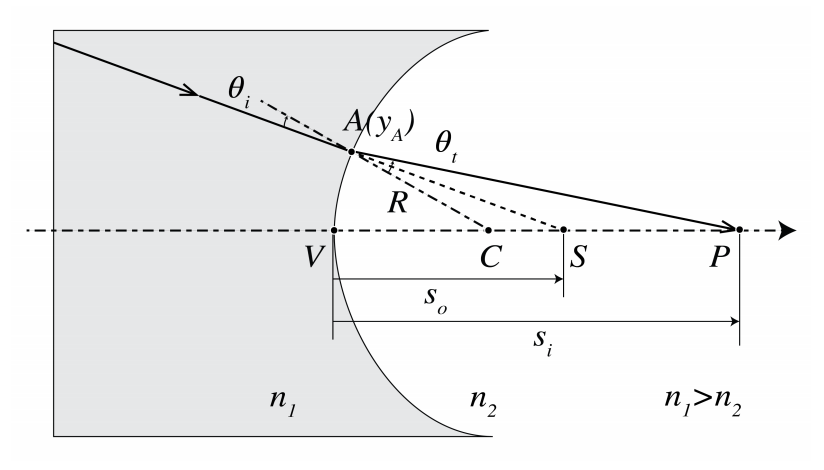
If \(n_1 > n_2\) or \(R < 0\) (i.e. the surface is concave when seen from the left of the vertex), the right-hand side of (\(\PageIndex{2}\)) is negative:

\[\dfrac{n_{2}-n_{1}}{R}<0. \nonumber \]

Light rays incident from the left are then refracted away from the z-axis and incident rays that are parallel to the z-axis are refracted such that they never intersect the z-axis in medium 2. Instead, they seem to be emitted by a point in medium 1. As illustrated in Figure \(\PageIndex{2}\), the second focal point is thus virtual with negative focal length given by:

\[f_{i}=\dfrac{n_{2}R}{n_{2}-n_{1}}<0. \nonumber \]

Furthermore, f_o > 0 and an incident ray that after refraction is parallel to the z-axis in medium 2 seems for an observer in medium 1 to converge to a point in medium 2. Hence the first focal point is virtual as well: f_o > 0. When (\(\PageIndex{12}\)) holds, for all object points S in front of the lens (s_o < 0), the image point is always virtual. In fact, si as given by (\(\PageIndex{2}\)) is then always negative.

2.5.2 Ray Vectors and Ray Matrices

In geometrical optics it is convenient to use ray vectors and ray matrices. In any plane perpendicular to the z-axis, a ray is determined by the y-coordinate of the point of intersection of the ray with the plane and the acute angle α of the ray with the z-axis. Here y > 0 when the intersection point is above the z-axis and y < 0 otherwise. We define the ray vector

\[\dbinom{nα}{y}, \nonumber \]

where n is the local refractive index. The definition with the refractive index as factor in the first element of the ray vector turns out to be convenient. The acute angle α has sign according to the convention in Table \(\PageIndex{1}\).

The ray vectors of a ray in any two planes z = z₁, z = z₂, with z₂ > z₁, are related by a so-called ray matrix:

\[\dbinom{n_{2}α_{2}}{y_{2}}=M\dbinom{n_{1}α_{1}}{y_{1}}. \nonumber \]

where

\[M=\begin{pmatrix} A & B \\ C & D \end{pmatrix}. \nonumber \]

The elements of matrix M depend on the optical components and materials between the planes z = z₁ and z = z₂.

As an example consider the ray matrix that relates a ray vector in the plane immediately before the spherical surface in Figure \(\PageIndex{2}\) to the corresponding ray vector in the plane immediately behind that surface. Using (\(\PageIndex{5}\)) and (\(\PageIndex{7}\)) it follows

\[n_{1}α_{1}-n_{2}α_{2}=\dfrac{(n_{2}-n_{1})y_{1}}{R}, \nonumber \]

where we have replaced α₂ by −α₂ in (\(\PageIndex{5}\)), because according to the sign convention, the angle α₂ in Figure \(\PageIndex{1}\) should be taken negative. Because furthermore y₂ = y₁, we conclude

\[\dbinom{n_{2}α_{2}}{y_{2}}=\dbinom{n_{1}α_{1}-\dfrac{(n_{2}-n_{1})y_{1}}{R}}{y_{1}}=\begin{pmatrix} 1 & -P \\ 0 & 1 \end{pmatrix}\dbinom{n_{1}α_{1}}{y_{1}},spherical\space surface, \nonumber \]

where

\[P=\dfrac{n_{2}-n_{1}}{R}, \nonumber \]

is called the power of the surface.

For a spherical mirror with radius of curvature R, we see that

\[α_{1}=θ_{i} − ϕ, \nonumber \]

\[α_{2}=-θ_{r} − ϕ, \nonumber \]

where we take the sign convention for the angles into account. Because θ_r = θ_i we find

\[α_{2}=-α_{1}+2ϕ=-α_{1}+2\dfrac{y_{1}}{R}, \nonumber \]

where we used (\(\PageIndex{7}\)) with y_A = y₁. As mentioned in Table \(\PageIndex{1}\), the refractive index after reflection is to be chosen negative. This means that for rays that propagate from right to left, the refractive index in the ray vector should be chosen negative. Hence,

\[n_{2}α_{2}=-n_{1}α_{2}= n_{1}α_{1} -2n_{1}\dfrac{y_{1}}{R}. \nonumber \]

Then

\[\dbinom{n_{2}α_{2}}{y_{2}}=\begin{pmatrix} 1 & -P \\ 0 & 1 \end{pmatrix}\dbinom{n_{1}α_{1}}{y_{1}},spherical\space reflector, \nonumber \]

where

\[P=\dfrac{2n_{1}}{R} \nonumber \]

is the power of the mirror. We conclude that the ray matrix for reflection by a spherical mirror is the same as that for refraction by a spherical surface, provided that n₂ is replaced by −n₁. When a ray is propagating from the right to the left, the refractive index of all media and interfaces through which the ray propagates, and at which it is being refracted, should have negative refractive index. After the ray has been reflected a second time, due to which it propagates again from left to right, all refractive indices should again be positive. In this way the matrix method can be applied to optical systems consisting of both refracting elements, such as lenses, and reflecting elements.

Finally we consider the case that between the two planes there is homogeneous material with refractive index n. In that case α₂ = α₁ and y₂ = y₁ + α₁(z₂ − z₁), hence

\[M=\begin{pmatrix} 1 & 0 \\ \dfrac{z_{2}-z_{1}}{n} & 1 \end{pmatrix},homogeneous\space space. \nonumber \]

For two planes between which there are a number of optical components, possibly separated by regions with homogeneous material (e.g. air), the ray matrix can be obtained by multiplying the matrices of the individual components and of the homogeneous regions. The order of the multiplication of the matrices is such that the right-most matrix corresponds to the first component that is encountered while propagating, and so on.

It should be remarked that the rays considered in the ray matrix approach stay in the same plane, namely the plane through the ray and the z-axis. These rays are called meridional rays. By considering only meridional rays, the imaging by optical systems is restricted to two dimensions. Non-meridional rays are called skew rays. Skew rays do not pass through the optical axis and they are not considered in the paraxial theory.

2.5.3 The Lens Matrix

We apply ray matrices to a lens. Figure \(\PageIndex{4}\) shows a lens with two spherical surfaces. The refractive index of the lens is n_l and that of the ambient medium is n_m and the distance between the vertices is d. We will first derive the matrix which maps the ray vector in the plane immediately in front of the lens to that in the plane immediately behind the lens. Let

\[\dbinom{n_{m}α_{1}}{y_{1}}and\dbinom{n_{m}α_{2}}{y_{2}} \nonumber \]

be two vectors in the two planes which correspond to the same ray. The ray is first refracted by the spherical surface with radius R₁ and centre C₁. Using (\(\PageIndex{25}\)) and (\(\PageIndex{20}\)) it follows that the matrix between the ray vectors just before and just behind the spherical surface with radius R₁ and centre C₁ is given by

\[M_{1}=\begin{pmatrix} 1 & -\dfrac{ n_{l} - n_{m} }{R_{1}} \\ 0 & 1 \end{pmatrix} \nonumber \]

The ray propagates then over the distance d through the material of which the lens is made. The matrix that maps ray vectors from the plane inside the lens immediately behind the left spherical surface to a ray vector in the plane immediately before the right spherical surface follows from (\(\PageIndex{27}\)):

\[M=\begin{pmatrix} 1 & 0 \\ \dfrac{d}{n_{l}} & 1 \end{pmatrix}. \nonumber \]

Finally, the matrix that maps ray vectors from the plane in the lens immediately before the second spherical surface to vectors in the plane immediately behind it is

\[M_{1}=\begin{pmatrix} 1 & -\dfrac{ n_{m} - n_{l} }{R_{2}} \\ 0 & 1 \end{pmatrix}. \nonumber \]

Hence the matrix that maps ray vectors in the plane immediately before the lens to ray vectors in the plane immediately behind the lens is given by the matrix product:

\[M=M_{3}M_{2}M_{1}=\begin{pmatrix} 1-\dfrac{d}{n_{l}}P_{2} & -P_{1}-P_{2}+\dfrac{d}{n_{l}}P_{1}P_{2} \\ \dfrac{d}{n_{l}} & 1-\dfrac{d}{n_{l}}P_{1} \end{pmatrix},lens, \nonumber \]

where

\[P_{1}=\dfrac{ n_{l} - n_{m} }{R_{1}},P_{2}=\dfrac{ n_{m} - n_{l} }{R_{2}}. \nonumber \]

The quantity

\[P=P_{1}+P_{2}-\dfrac{d}{n_{l}}P_{1}P_{2} \nonumber \]

is called the power of the lens. It has dimension 1/length and is given in diopter (D), where 1 D = m⁻¹. The power can be positive and negative. The z-axis is the axis of symmetry and is called the optical axis. The space to the left of the lens is called the object space and that to the right of the lens is called the image space.

Figure \(\PageIndex{3}\): A spherical lens made of glass of index n_l in a medium of index n_m. The point S is imaged in P.

2.5.4 Focusing with a Thin Lens

For a thin lens the vertices V₁ and V₂ coincide and d = 0, hence (\(\PageIndex{34}\)) becomes

\[M=\begin{pmatrix} 1 & -P \\ 0 & 1 \end{pmatrix},thin\space lens, \nonumber \]

where P = P₁ + P₂, with P₁ and P₂ given by (\(\PageIndex{35}\)). The origin of the coordinate system is chosen in the common vertex V₁ = V₂. For a ray emerging in image space at height y₂ and parallel to the optical axis: α₂ = 0, we have y₁ = y₂ and

\[n_{m} α _{1}=P_{y}. \nonumber \]

If the power is positive: P > 0, the angle α1 has the same sign as y₁, which implies that the ray in object space has intersected the optical axis in a point F_o with z-coordinate: z = f_o satisfying

\[\dfrac{1}{f_{o}}=\dfrac{α _{1}}{y _{1}} = \dfrac{n_{m}}{P}=\dfrac{n_{l}-n_{m}}{n_{m}}(\dfrac{1}{R_{1}}-\dfrac{1}{R_{2}}). \nonumber \]

The point Fo is called the first focal point or object focal point.

Similarly, by considering a ray in medium 1 which is parallel to the optical axis (α₁ = 0) and at height y₁, we get n_mα₂ = −P y₁ and y₂ = y₁. Hence, when P > 0, the angle α₂ of the ray has sign opposite to y₂ and therefore the ray in image space is bent back to the optical axis, yielding a second focal point or image focal point F_i. Its z-coordinate f_i satisfies:

\[\dfrac{1}{f_{i}}=-\dfrac{α _{2}}{y _{2}} = -\dfrac{n_{m}}{P}=-\dfrac{1}{f_{o}}. \nonumber \]

When the power P of the lens is positive, f_i = −f_o > 0, which means that the first and second focal points are in the object and image space, respectively. A lens with positive power is called convergent or positive.

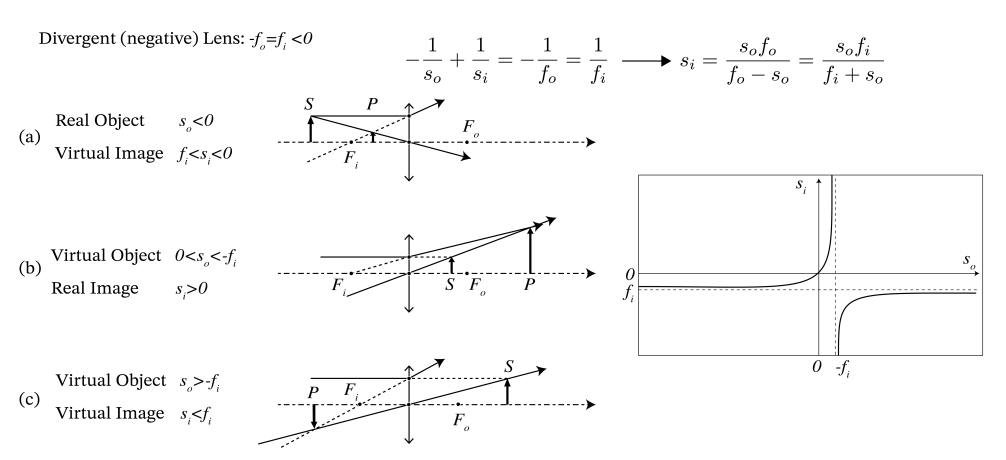
A lens with negative power is called divergent and has f_i = −f_o < 0. Then incident rays parallel to the optical axis are refracted away from the optical axis and seem to come from a point in front of the lens with z-coordinate f_i < 0. Hence the second focal point does not correspond to a location where there is actual concentration of light intensity and hence it is virtual. The first focal point is a virtual object point, because only for a bundle of incident rays that are converging to a certain point behind the lens, the negative refraction can give a bundle of rays that are all parallel to the optical axis.

With the results obtained for the focal coordinates we can rewrite the lens matrix of a thin lens alternatively as

\[M=\begin{pmatrix} 1 & -\dfrac{n_{m}}{f_{i}} \\ 0 & 1 \end{pmatrix},thin\space lens. \nonumber \]

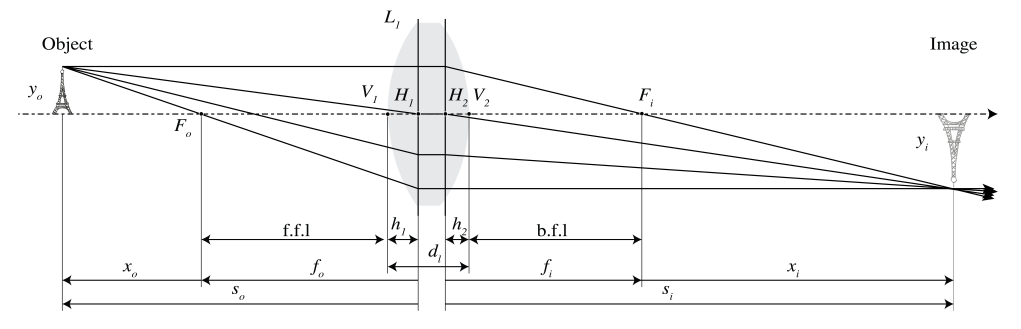
2.5.5 Imaging with a Thin Lens

We first consider the general ray matrix (\(\PageIndex{16}\)), (\(\PageIndex{17}\)) between two planes z = z₁ and z = z₂ and ask the following question: what are the properties of the ray matrix such that the two planes are images of each other, or (as this is also called) are each other’s conjugate? Clearly for these planes to be each other’s image, we should have that for every point coordinate y₁ in the plane z = z₁, there is a point with coordinate y₂ in the plane z = z₂ such that any ray through (y₁, z₁) (within some cone of rays) will pass through point (y₂, z₂). Hence for any angle α₁ (in some interval of angles) there is an angle α₂ such that (\(\PageIndex{16}\)) is valid. This means that for any y₁ there is a y₂ such that for all angles α₁:

\[y _{2}=Cn_{1}α _{1}+Dy _{1}, \nonumber \]

This requires that

\[C = 0, condition\space for\space imaging. \nonumber \]

The ratio of y₂ and y₁ gives the magnification. Hence

\[\dfrac{y _{2}}{y _{1}}=D, \nonumber \]

is the magnification of the image (this quantity has sign).

To determine the image of a point by a thin lens we first derive the ray matrix between the planes z = z₁ < 0 and z = z₂ > 0 with a thin lens in between with vertex at the origin. This matrix is the product of the matrix for propagating from z = z₁ to the plane immediately in front of the lens, the matrix of the thin lens and the matrix for propagation from the plane immediately behind the lens to the plane z = z₂:

\[M=\begin{pmatrix} 1 & 0 \\ \dfrac{z _{2}}{n _{m}} & 1 \end{pmatrix}\begin{pmatrix} 1 & -\dfrac{n _{m}}{f_{i}} \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ -\dfrac{z _{1}}{n _{m}} & 1 \end{pmatrix}=\begin{pmatrix} 1+\dfrac{z _{1}}{f_{i}} & -\dfrac{n _{m}}{f_{i}} \\ -\dfrac{z _{1}}{n _{m}}+\dfrac{z _{2}}{n _{m}}+\dfrac{z _{1}z _{2}}{n _{m}f_{i}} & 1-\dfrac{z _{2}}{f _{i}} \end{pmatrix} \nonumber \]

The imaging condition (\(\PageIndex{41}\)) implies:

\[-\dfrac{1}{s _{o}}+\dfrac{1}{s _{i}}=\dfrac{1}{f _{i}},Lensmaker's\space Formula. \nonumber \]

where we have written s_o = z₁ and s_i = z₂ for the z-coordinates of the object and the image. Because for the thin lens matrix (\(\PageIndex{43}\)): D = 1− z₂/f_i , it follows by using (\(\PageIndex{44}\)) that the magnification (\(\PageIndex{42}\)) is given by

\[M=\dfrac{y _{i}}{y _{o}}=1-\dfrac{s _{i}}{f _{i}}=\dfrac{s _{i}}{s _{o}}, \nonumber \]

where we have written now y_o and y_i instead of y₁ and y₂, respectively.

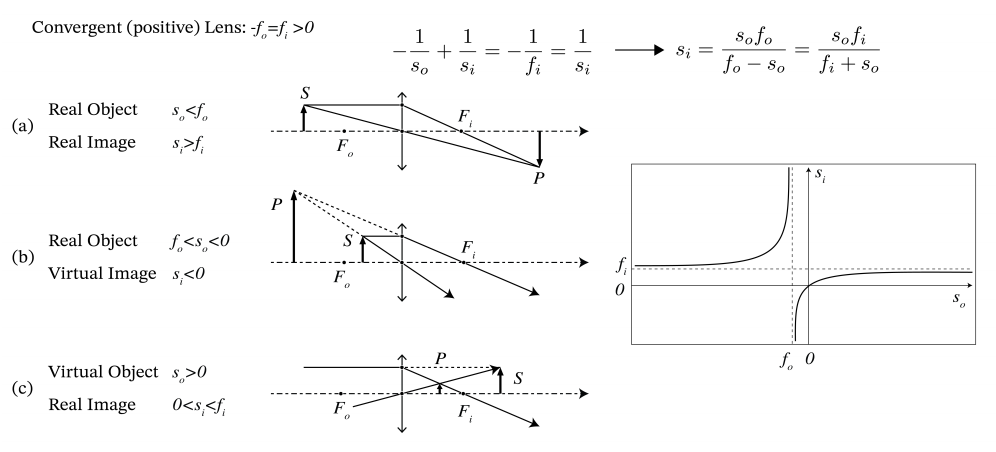
For a positive lens: f_i > 0 and hence (\(\PageIndex{44}\)) implies that s_i > 0 provided |s_o| < f_i = |f_o|, which means that the image by a convergent lens is real if the object is further from the lens than the first focal point F_o. The case s_o > 0 corresponds to a virtual object, i.e. to the case of a converging bundle of incident rays, which for an observer in object space seems to converge to a point at distance so behind the lens. A convergent lens (f_i > 0) will then make an image between the lens and the second focal point. In contrast, a diverging lens (f_i < 0) can turn the incident-converging bundle into a real image only if the virtual object point is between the lens and the focal point. If the virtual object point has larger distance to the lens, the convergence of the incident bundle is too weak and the diverging lens then refracts this bundle into a diverging bundle of rays with vertex at the virtual image point in front of the lens (s_i < 0).

One can also construct the image with a ruler. Consider imaging a finite object S₁S₂ as shown in Figure \(\PageIndex{4}\). Let y_o be the y-coordinate of S₂. We have y_o > 0 when the object is above the optical axis. Draw the ray through the focal point F_o in object space and the ray through the centre V of the lens. The first ray becomes parallel in image space. The latter intersects both surfaces of the lens almost in their (almost coinciding) vertices and therefore the refraction is opposite at both surfaces and the ray exits the lens parallel to its direction of incidence. Furthermore, its lateral displacement can be neglected because the lens is thin. Hence, the ray through the centre of the lens is not refracted. The intersection in image space of the two rays gives the location of the image point P₂ of S₂. The image is real if the intersection occurs in image space and is virtual otherwise. For the case of a convergent lens with a real object with y_o > 0 as shown in Figure \(\PageIndex{4}\), it follows from the similar triangles ∆ AVF_i and ∆ P₂P₁F_i that

\[\dfrac{y _{o}}{|y _{i}|}=\dfrac{f _{i}}{s _{i}-f _{i}}, \nonumber \]

where we used |f_o| = f_i. From the similar triangles ∆ S₂S₁F_o and ∆ BVF_o:

\[\dfrac{|y _{i}|}{y _{o}}=\dfrac{f _{i}}{f _{o}-s _{o}}. \nonumber \]

(the absolute value of y_i is taken because according to our sign convention y_i in Figure \(\PageIndex{4}\) is negative whereas (\(\PageIndex{44}\)) is a ratio of lengths). By multiplying these two equations we get the Newtonian form of the lens equation:

\[x _{o}x _{i}=-f _{i}^2=-f _{o}^2, \nonumber \]

where x_o and x_i are the z-coordinates of the object and image relative to those of the first and second focal point, respectively:

\[x _{o}=s _{o}-f _{o},x _{i}=s _{i}-f _{i}. \nonumber \]

Figure \(\PageIndex{4}\): Object and image for a thin lens.

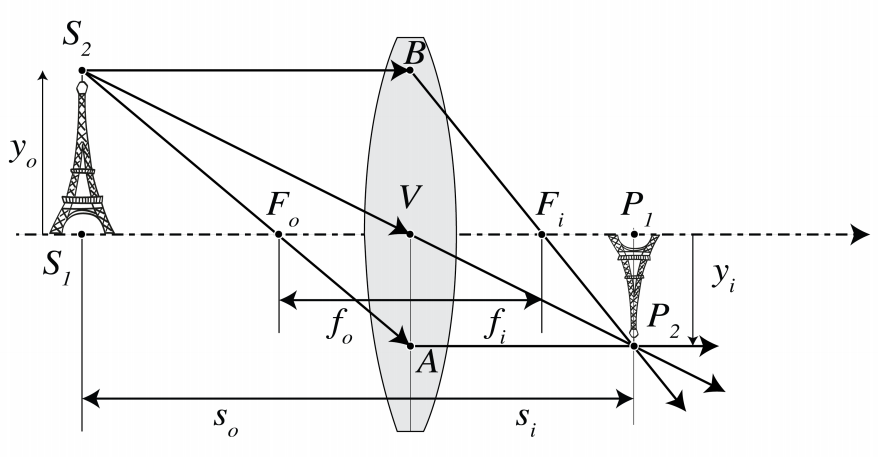
Hence x_o is negative if the object is t_o the left of F_o and x_i is positive if the image is to the right of F_i.

The transverse magnification is

\[M=\dfrac{y _{i}}{y _{o}}=\dfrac{s _{i}}{s _{o}}= -\dfrac{x _{i}}{f _{i}} , \nonumber \]

where the second identity follows from considering the similar triangles ∆P₂P₁F_i and ∆AVF_i in Figure \(\PageIndex{4}\). A positive M means that the image is erect, a negative M means that the image is inverted (as is always the case for a single lens).

All equations are also valid for a thin negative lenses and for virtual objects and images. Some examples of real and virtual object and image points for a positive and a negative lens are shown in Figs. \(\PageIndex{5}\) and \(\PageIndex{6}\).

2.5.6 Two Thin Lenses

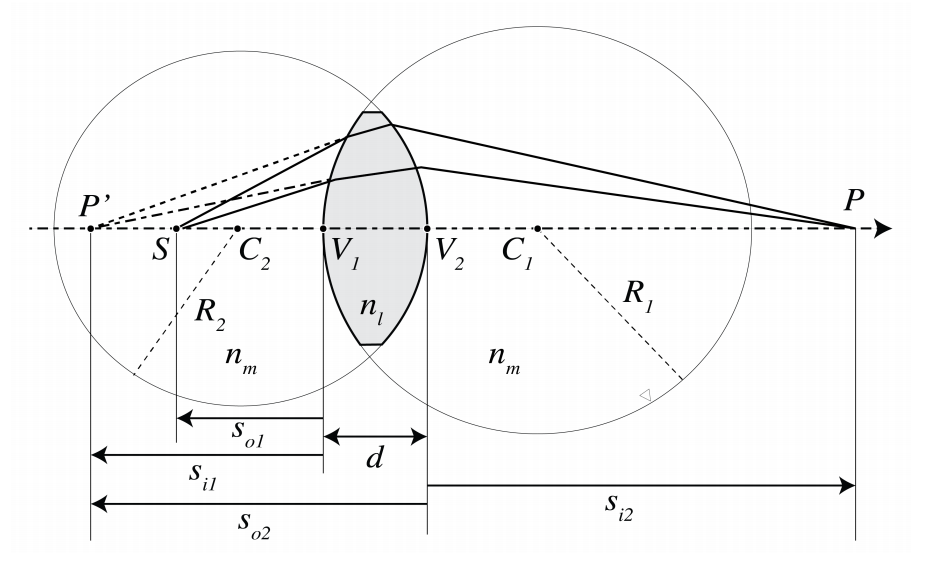
The imaging by two thin lenses L₁ and L₂ can easily be obtained by construction. We simply construct the image obtained by the first lens as if the second lens were not present and use this image as (possibly virtual) object for the second lens. In Figure \(\PageIndex{7}\) an example is shown where the distance between the lenses is larger than the sum of their focal lengths. First the image P' of S is constructed as obtained by L₁ as if L₂ were not present. We construct the intermediate image P' due to lens L₁ using ray 2 and 3. P₁ is a real image of lens L₁ which is also real object for lens L₂. Ray 3 is parallel to the optical axis between the two lenses and is thus refracted by lens L2 through its back focal point F_2i. Ray 4 is the ray from P1 through the centre of lens L₂. The image point P is the intersection of ray 3 and 4.

In the case of Figure \(\PageIndex{8}\) the distance d between the two positive lenses is smaller than their focal lengths. The intermediate image P' is a real image for L₁ obtained as the intersection of rays 2 and 3 passing through the object and image focal points F_1o and F_1i of lens L₁. P' is now a virtual object point for lens L₂. To find its image by L₂, draw ray 4 from P' through the centre of lens L₂ back to S (this ray is refracted by lens L₁ but not by L₂) and draw ray 3 as refracted by lens L₂. Since ray 3 is parallel to the optical axis between the lenses, it passes through the back focal point F_2i of lens L₂. The intersection point of ray 3 and 4 is the final image point P.

Figure \(\PageIndex{5}\): Real and virtual objects and images for a convergent thin lens, i.e. −f_o = f_i > 0. In (a) the object is real with s_o < f_o and the image is real as well (s_i > 0). In (b) the object is between the focal point in front of the lens and the lens: f_o < s_o < 0. Then the rays from the object are too divergent for the lens to make them convergent in image space and the image is virtual: s_i < 0. In (c) there is a cone of converging rays incident on the lens from the left which, in the absence of the lens, would converge to point S behind the lens. Hence S is a virtual object (s₀ > 0). The image is real and can be constructed with the two rays shown. In (d) si is shown as function of so for a convergent lens (see Eq. (\(\PageIndex{44}\))).

Figure \(\PageIndex{6}\): Real and virtual objects and images for a divergent thin lens, i.e. −f_o = f_i < 0. In (a) the object is real, i.e. s_o < 0. The diverging lens makes the cone of rays from the object more divergent so that the image is virtual: s_i < 0. When the object is virtual, there is a cone of converging rays incident from the left which after extension to the right of the lens (as if the lens is not present) intersect in the virtual object S (s_o > 0). It depends on how strong the convergence is whether the diverging lens turns this cone into converging rays or whether the rays keep diverging. In (b) 0 < s_o < −f_i , and the image is real. In c) s_o > −f_i and the image is real (s_i > 0). In (d) si is shown as function of so for a divergent lens (f_i < 0 (see Eq.‘(\(\PageIndex{44}\))).

Figure \(\PageIndex{7}\): Two thin lenses separated by a distance that is larger than the sum of their focal lengths.

Figure \(\PageIndex{8}\): Two thin lenses at a distance smaller than their focal lengths.

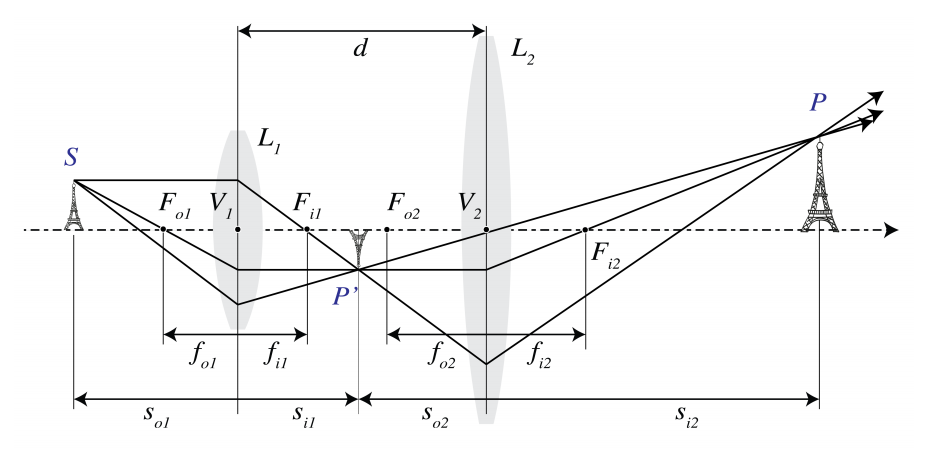
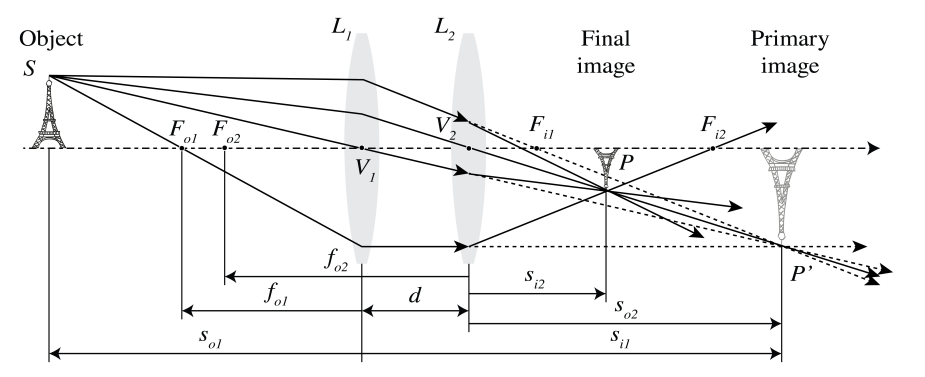
It is easy to express the z-coordinate s_i with respect to the coordinate system with origin at the vertex of L₂ of the final image point, in the z-component s_o with respect to the origin at the vertex of lens L₁ of the object point. We use the Lensmaker’s Formula for each lens while taking care that the proper local coordinate system is used in each case. The intermediate image P' due to lens L₁ has z-coordinate s_1i with respect to the coordinate system with origin at the vertex V₁, which satisfies:

\[\dfrac{1}{s_{o}}+\dfrac{1}{s_{1i}}=\dfrac{1}{f_{1i}}. \nonumber \]

P' is object for lens L₂ with z-coordinate with respect to the coordinate system with origin at V₂ given by: s_2o = s_1i − d, where d is the distance between the lenses. Hence, with s_i = s_2i the Lensmaker’s Formula for lens L₂ implies:

\[-\dfrac{1}{s_{1i}-d}+\dfrac{1}{s_{i}}= \dfrac{1}{f_{2i}}. \nonumber \]

By solving (\(\PageIndex{51}\)) for s_1i and substituting the result into (\(\PageIndex{52}\)), we find

\[s_{i}=\dfrac{-df_{1i} f_{2i}+ f_{2i}( f_{1i} -d)s_{o} }{ f_{1i}( f_{2i} -d) +( f_{1i}+ f_{2i} -d)s_{o} },two\space thin\space lenses. \nonumber \]

By taking the limit s_o → −∞, we obtain the z-coordinate f_i of the image focal point of the two lenses, while s_i → ∞ gives the z-coordinate f_o of the object focal point:

\[f_{i}=\dfrac{( f_{1i} -d) f_{2i} }{ f_{1i}+ f_{2i} -d}, \nonumber \]

\[f_{o}=-\dfrac{( f_{2i} -d) f_{1i} }{ f_{1i}+ f_{2i} -d}, \nonumber \]

Except when the refractive indices of the media before and after the lens are different, the object and image focal lengths of a thin lens are the same. However, as follows from the derived formula for an optical system with two lenses, the object and image focal lengths are in general different when there are several lenses.

By construction using the intermediate image, it is clear that the magnification of the two-lens system is the product of the magnifications of the two lenses:

\[M=M_{1}M_{2}. \nonumber \]

Remarks

1. When f_1i + f_2i = d the focal points are at infinity. Such a system is called telecentric.

2. In the limit where the lenses are very close together: d → 0, (\(\PageIndex{53}\)) becomes

\[-\dfrac{1}{s_{o}}+\dfrac{1}{s_{i}}= \dfrac{1}{f_{1i}}+ \dfrac{1}{f_{2i}}. \nonumber \]

The focal length fi of the system of two lenses in contact thus satisfies:

\[\dfrac{1}{f_{i}}=\dfrac{1}{f_{1i}}+\dfrac{1}{f_{2i}}. \nonumber \]

Two positive lenses in close contact enforce each other, i.e. the second positive lens makes the convergence of the first lens stronger. Similarly, two negative lenses in contact make a more strongly negative system. The same applies for more than two lenses in close contact.

3. Although for two lenses the image coordinate can still be expressed relatively easily in the object distance, for systems with more lenses finding the overall ray matrix and then using the image condition (\(\PageIndex{41}\)) is a much better strategy.

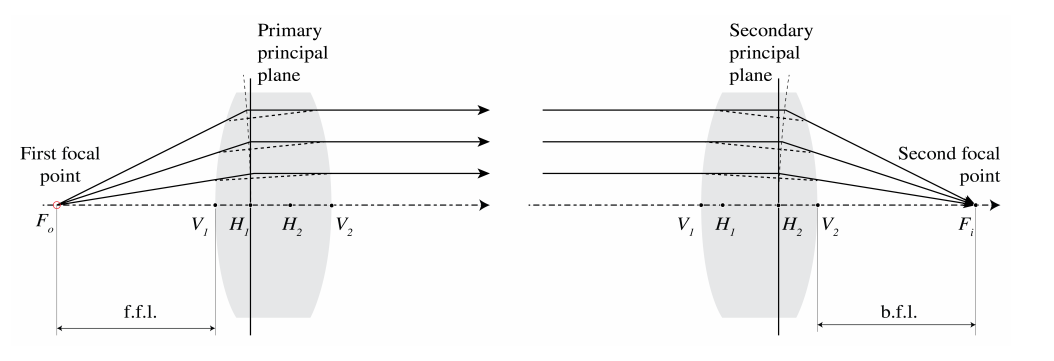
2.5.7 The Thick Lens

At the left of Figure \(\PageIndex{9}\) a thick lens is shown. The first focal point is defined as the point whose rays are refracted such that the emerging rays are parallel to the optical axis. By extending the incident and emerging rays by straight segments, the points of intersection are found to be on a curved surface, which close to the optical axis, that is in the paraxial approximation, is in good approximation a plane perpendicular to the optical axis. This plane is called the primary principal plane and its intersection with the optical axis is called the primary principal point H₁. By considering incident rays which are parallel to the optical axis and therefore focused in the back focal point, the secondary principal plane and secondary principal point H₂ are defined in a similar way (see the drawing at the right in Figure \(\PageIndex{9}\)). The principal planes need not be inside the lens. In particular for meniscus lenses, this is not the case. It can be seen from Figure 2.18 that the principal planes are images of each other, with unit magnification. Hence, if an object is placed in the primary principal plane (hypothetically if this plane is inside the lens), its image is in the secondary principal plane. The image is erect and has unit magnification.

Figure \(\PageIndex{9}\): Principal planes of a thick lens, with front and back focal lengths: f.f.l and b.f.l.

Figure \(\PageIndex{10}\): Position of the principal planes for several lenses.

We recall the result (\(\PageIndex{32}\)) for the ray matrix between the planes through the front and back vertices V₁, V₂ of a thick lens with refractive index n_l and thickness d:

\[M_{V_{1}V_{2}}=\begin{pmatrix} 1-\dfrac{d}{n_{l}}P_{2} & -P \\ \dfrac{d}{n_{l}} & 1-\dfrac{d}{n_{l}}P_{1} \end{pmatrix},thick\space lens, \nonumber \]

where

\[P_{1}=\dfrac{n_{l}-n_{m}}{R_{1}},P_{2}=\dfrac{n_{m}-n_{l}}{R_{2}}, \nonumber \]

and n_m is the refractive index of the ambient medium, and

\[P=P_{1}+P_{2}-\dfrac{d}{n_{l}}P_{1}P_{2}. \nonumber \]

If h₁ is the z-coordinate of the first principal point H₁ with respect to the coordinate system with origin vertex V₁, we have according to (\(\PageIndex{27}\)) for the ray matrix between the primary principal plane and the plane through vertex V₁

\[M_{1}=\begin{pmatrix} 1 & 0 \\ \dfrac{h_{1}}{n_{m}} & 1\end{pmatrix}. \nonumber \]

Similarly, if h₂ is the coordinate of the secondary principal point H₂ with respect to the coordinate system with V₂ as origin, the ray matrix between the plane through vertex V₂ and the secondary principal plane is

\[M_{2}=\begin{pmatrix} 1 & 0 \\ \dfrac{h_{2}}{n_{m}} & 1\end{pmatrix}. \nonumber \]

The ray matrix between the two principle planes is then

\[M_{H_{1}H_{2}}=M_{2}M_{V_{1}V_{2}}M_{1}. \nonumber \]

The coordinates h1 and h2 can be found by imposing to the resulting matrix the imaging condition (\(\PageIndex{41}\)): C = 0 and the condition that the magnification should be unity: D = 1, which follows from (\(\PageIndex{42}\)). We omit the details and only give the resulting expressions here:

\[h_{1}=\dfrac{n_{m}}{n_{l}}\dfrac{P_{2}}{P}d, \nonumber \]

\[h_{2}=-\dfrac{n_{m}}{n_{l}}\dfrac{P_{1}}{P}d. \nonumber \]

Furthermore, (\(\PageIndex{64}\)) becomes

\[M_{H_{1}H_{2}}=\begin{pmatrix} 1 & -P \\ 0 & 1\end{pmatrix}. \nonumber \]

We see that the ray matrix between the principal planes is identical to the ray matrix of a thin lens (\(\PageIndex{35}\)). We therefore conclude that if the coordinates in object space are chosen with respect to the origin in the primary principal point H₁, and the coordinates in image space are chosen with respect to the origin in the secondary principal point H₂, the expressions for the first and second focal points and for the coordinates of the image point in terms of that of the object point are identical to that for a thin lens. An example of imaging by a thick lens is shown in Figure \(\PageIndex{11}\).

Figure \(\PageIndex{11}\): Thick-lens geometry. There holds f_i = f_o if the ambient medium left of the lens is the same as to the right of the lens.

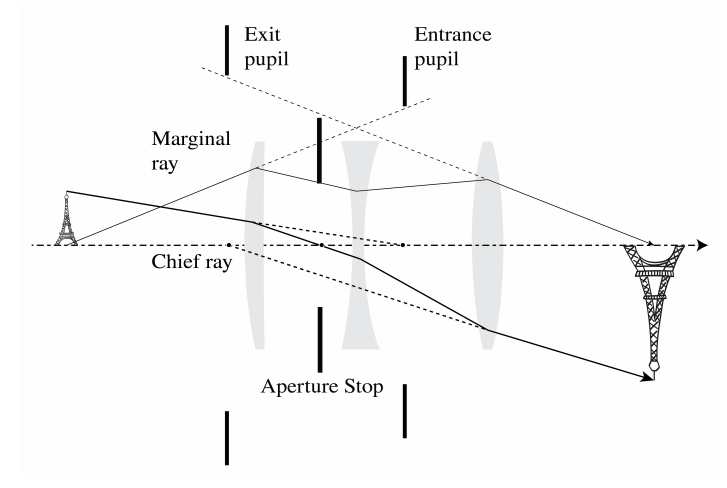
2.5.8 Stops

An element such as the rim of a lens or a diaphragm which determines the set of rays that can contribute to the image, is called the aperture stop. An ordinary camera has a variable diaphragm.

The entrance pupil is the image of the aperture stop by all elements to the left of the aperture stop. If there are no lenses between object and aperture stop, the aperture stop itself is the entrance pupil. Similarly the exit pupil is the image of the aperture stop by all elements to the right of it. The entrance pupil determines for a given object the cone of rays that enters the optical system, while the cone of rays leaving and taking part in the image formation is determined by the exit pupil (see Figure \(\PageIndex{12}\)). Note that in constructing the entrance pupil as the image of the aperture stop by the lenses to the left of it, are propagating from the right to the left. Hence the aperture stop is a real object in this construction, while the entrance pupil can be a real or a virtual image. The rays used in constructing the exit pupil as the image of the aperture stop by the lenses following the stop are propagating from the left to the right. Hence also in this case the aperture stop is a real object while the exit pupil can be a real or a virtual image of the aperture stop.

For any object point, the chief ray is the ray in the cone that passes through the centre of the entrance pupil, and hence also through the centres of the aperture stop and the exit pupil. A marginal ray is the ray that for an object point on the optical axis passes through the rim of the entrance pupil (and hence also through the rims of the aperture stop and the exit pupil).

For a fixed diameter D of the exit pupil and given x_o, the magnification of the system is according to (\(\PageIndex{50}\)) and (\(\PageIndex{48}\)) given by M = −x_i/f_i = f_i/x_o. It follows that when fi is increased, the magnification increases. A larger magnification means a lower energy density, hence a longer exposure time, i.e. the speed of the lens is reduced. Camera lenses are usually specified by two numbers: the focal length f_i and the diameter D of the exit pupil. The f-number is the ratio of the focal length to this diameter:

\[f-number=\dfrac{f}{D}. \nonumber \]

For example, f-number= 2 means f = 2D. Since the exposure time is proportional to the square of the f-number, a lens with f-number 1.4 is twice as fast as a lens with f-number 2.

Figure \(\PageIndex{1}\): Aperture stop (A.S.) between the second and third lens, with entrance pupil and exit pupil (in this case these pupils are virtual images of the aperture stop). Also shown are the chief ray and the marginal ray.