5.2: Antiparticles
( \newcommand{\kernel}{\mathrm{null}\,}\)
Both the Klein-Gordon and the Dirac equation have a really nasty property. Since the relativistic energy relation is quadratic, both equations have, for every positive energy solution, a negative energy solution. We don’t really wish to see such things, do we? Energies are always positive and this is a real problem. The resolution is surprisingly simple, but also very profound – It requires us to look at the problem in a very different light.
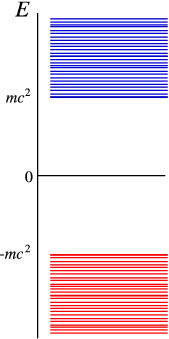
In Figure 5.2.1 we have sketched the solutions for the Dirac equation for a free particle. It has a positive energy spectrum starting at mc2 (you cannot have a particle at lower energy), but also a negative energy spectrum below −mc2. The interpretation of the positive energy states is natural – each state describes a particle moving at an energy above mc2. Since we cannot have negative energy states, their interpretation must be very different. The solution is simple: We assume that in an empty vacuum all negative energy states are filled (the “Dirac sea”). Excitations relative to the vacuum can now be obtained by adding particles at positive energies, or creating holes at negative energies. Creating a hole takes energy, so the hole states appear at positive energies. They do have opposite charge to the particle states, and thus would correspond to positrons! This shows a great similarity to the behaviour of semiconductors, as you may well know. The situation is explained in Figure 5.2.2.
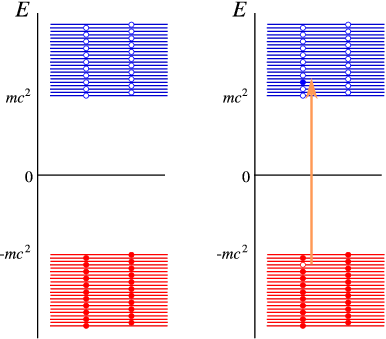
Note that we have ignored the infinite charge of the vacuum (actually, we subtract it away assuming a constant positive background charge.) Removing infinities from calculations is a frequent occurrence in relativistic quantum theory (RQT). Many unmeasurable quantities become infinite, and we are only interested in the finite part remaining after removing the infinities. This process is part of what is called renormalization, which is a systematic procedure to extract finite information from infinite answers!


