6.1: Non-normalizable Wavefunctions
( \newcommand{\kernel}{\mathrm{null}\,}\)
I have argued that solutions to the time-independent Schrödinger equation must be normalized, in order to have a the total probability for finding a particle of one. This makes sense if we think about describing a single Hydrogen atom, where only a single electron can be found. But if we use an accelerator to send a beam of electrons at a metal surface, this is no longer a requirement: What we wish to describe is the flux of electrons, the number of electrons coming through a given volume element in a given time.
Let me first consider solutions to the “free” Schrödinger equation, i.e., without potential, as discussed before. They take the form
ϕ(x)=Aeikx+Be−ikx.
Let us investigate the two functions. Remembering that
\hat{p}=\dfrac{ℏ}{i} \dfrac{∂}{∂ x}
we find that ϕ ( x ) (Equation \ref{6.1}) represents the sum of two states, one with momentum ℏ k, and the other with momentum −ℏ k. The first one describes a beam of particles going to the right, and the other term a beam of particles traveling to the left. A standing wavefunction associated with a bound state is when A= B (Figure \PageIndex{1}).
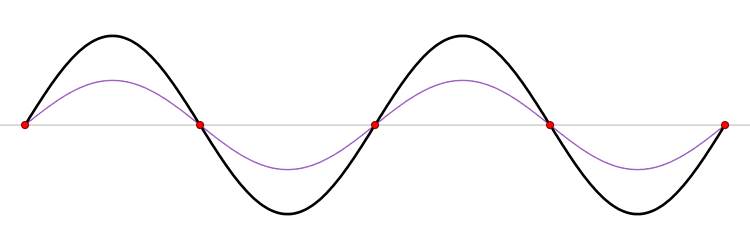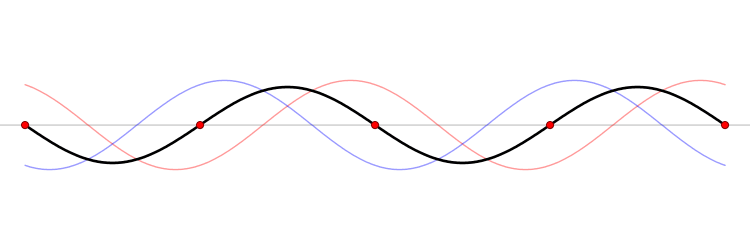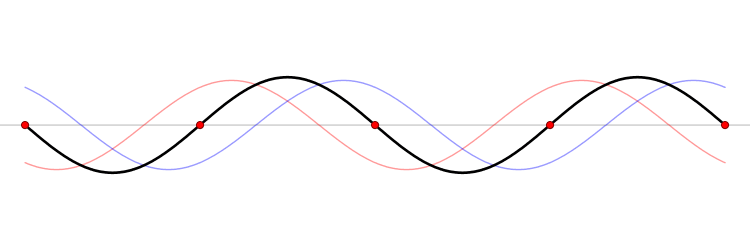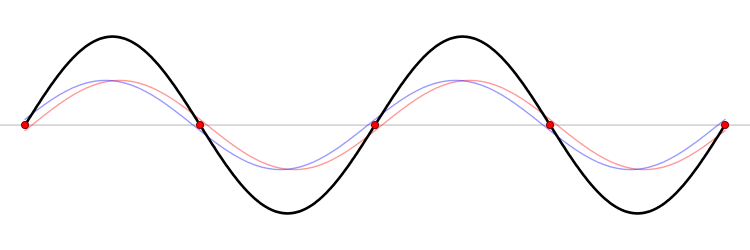
Figure \PageIndex{1}: A standing wave. The blue wave moves toward right while the red wave moves in the opposite direction. The combined wave (black) does not propagate
Let me concentrate on the first term, that describes a beam of particles going to the right. We need to define a probability current density. Since current is the number of particles times their velocity, a sensible definition is the probability density times the velocity,
| ϕ ( x ) |^2 \dfrac{ℏ k}{m} = | A |^2 \dfrac{ℏ k}{m} . \label{6.2}
This concept only makes sense for states that are not bound, and thus behave totally different from those I discussed previously.


