13.3: Complementarity and Copenhagen Interpretation
( \newcommand{\kernel}{\mathrm{null}\,}\)
Introduction
 Neils Bohr (1885 - 1962) was one of the giants in the development of Quantum Mechanics. He is best known for:
Neils Bohr (1885 - 1962) was one of the giants in the development of Quantum Mechanics. He is best known for:
- The development of the Bohr Model of the Atom in 1913. A small document on this topic is available here.
- The principle of Complementarity, the "heart" of Bohr's search for the significance of the quantum idea. This principle led him to:
- The Copenhagen Interpretation of Quantum Mechanics.
In this document we discuss Complementarity and then the Copenhagen Interpretation.
But first we shall briefly discuss the general issue of interpretations of Quantum Mechanics, and briefly describe two interpretations. The discussion assumes some knowledge of the Feynman Double Slit, such as is discussed here; it also assumes some knowledge of Schrödinger's Cat, such as is discussed here. Finally, further discussion of interpretations of Quantum Mechanics can be meaningfully given with some knowledge of Bell's Theorem; a document on that topic is here.
The level of discussion in what follows is based on an upper-year liberal arts course in modern physics without mathematics given at the University of Toronto. In that context, the discussion of Bell's Theorem mentioned in the previous paragraph is deferred until later.
A recommended reference on the material discussed below is:
F. David Peat, Einstein's Moon (Contemporary Books, 1990), ISBN 0-8092-4512-4 (cloth), 0-8092-3965-5 (paper).
Interpretations of Quantum Mechanics
Although the basic mathematical formalism of Quantum Mechanics was developed independently by Heisenberg and Schrödinger in 1926, a full and accepted interpretation of what that mathematics means still eludes us. If we found such an interpretation, then in some sense we could claim to understand Quantum Mechanics.
Richard Feynman stated that he never understood Quantum Mechanics. Certainly the author of this document does not understand Quantum Mechanics. This may be because Quantum Mechanics is not understandable, at least in the usual sense of the meaning of the word understandable.
Regrettably, some physicists claim that it is not important whether or not we understand Quantum Mechanics: what is important is that we know how to manipulate the mathematical formalism to get answers to our quantitative questions.
Here are some statements by physicists that take the opposite position on understanding:
- "Never make a calculation until you know the answer." -- Wheeler, Spacetime Physics, pg 60.
- "Our mathematical procedures seem to obscure our intuitive and imaginative understanding." -- Bohm, Foundations of Physics 5, 93 (1975).
- I feel that we do not have definite physical concepts at all if we just apply working mathematical rules; that's not what the physicist should be satisfied with." -- Dirac, Physicist's Conception of Nature, pg 11.
In any case, the typical education of a physicist tends to ignore the issue of interpretations.
To the extent that the usual course in Quantum Mechanics for physics students discusses interpretations at all, it usually presents only a simple probability view. Quantum Mechanics describes the world in terms of a "wave function" or "state function." When we see, say, electrons in a two slit experiment forming an interference pattern, we say that a wave has split up, gone through the two slits, and then re-combined. This is the normal way of explaining two slit interference of any type of wave. The Quantum Mechanical wave, the wave function, is interpreted as being the amplitude of the probability of finding the electron at some position in space. Thus, when we don't look at what is happening at the slits, there is a 50% chance a given electron went through the upper slit and a 50% chance it went through the lower slit. Thus the wave function has an amplitude at both slits, and then when later the wave functions re-combine we get interference. If we set up an experiment at the slits to see what the electrons are doing, we see each electron going through either the upper slit or through the lower slit, never through both slits at once. But the process of doing this measurement "collapses the wave function" so that it has a non-zero amplitude only at the slit where we see the electron. And it is this collapse that destroys the interference pattern.
Similarly, before we look the Quantum Mechanical description of Schrödinger's Cat states that after one half-life the cat is 50% alive and 50% dead. When we open the box and look we similarly "collapse the state."
Deeper consideration of this "interpretation" will quickly lead to the conclusion that it is at least incomplete.
Another interpretation of Quantum Mechanics was devised by Hugh Everett, III as a PhD thesis when he was a graduate student of John Wheeler at Princeton in 1957. The thesis itself was nine pages in length, which is about typical for the length of the bibliography of a typical PhD thesis in physics.
In Everett's interpretation when we, say, look in the box and find that Schrödinger's Cat is alive, that measurement has created a parallel universe where we found that the cat is dead. And similarly, every conscious act of perception bifurcates the universe.
In this view, then, when we find, say, a live cat the apparent fixed outcome is illusion, because we have created another parallel universe where we found a dead cat. And the totality is both universes, one with a live cat and the other with a dead one.
Borges' A Garden of Forking Paths evokes images reminiscent of the many-worlds interpretation:
" ... a picture, incomplete yet not false, of the universe as Ts'ui Pen conceived it to be. Differing from Newton and Schopenhauer, ... [he] did not think of time as absolute and uniform. He believed in an infinite series of times, in a dizzily growing, every spreading network of diverging, converging and parallel times. This web of time - the strands of which approach one another, bifurcate, intersect or ignore each other through the centuries - embraces every possibility. We do not exist in most of them. In some you exist and not I, while in others I do, and you do not, and in yet others both of us exist. In this one, in which chance has favored me, you have come to my gate. In another, you, crossing the garden, have found me dead. In yet another, I say these very same words, but am an error, a phantom."
Complementarity
Here is a favorite statement of Bohr's Principle of Complementarity, based on so-called wave-particle duality for light:
"But what is light really? Is it a wave or a shower of photons? There seems no likelihood for forming a consistent description of the phenomena of light by a choice of only one of the two languages. It seems as though we must use sometimes the one theory and sometimes the other, while at times we may use either. We are faced with a new kind of difficulty. We have two contradictory pictures of reality; separately neither of them fully explains the phenomena of light, but together they do." -- Albert Einstein and Leopold Infeld, The Evolution of Physics, pg. 262-263.
Incidentally, I have been told that Infeld wrote the entire book The Evolution of Physics in 1938, but was experiencing difficulty in getting anyone to publish it. Once Einstein put his name on it, all such difficulties disappeared.
John Wheeler, with his usual insight and striking prose, neatly summarizes the status of the principle:
"Bohr's principle of complementarity is the most revolutionary scientific concept of this century and the heart of his fifty-year search for the full significance of the quantum idea." -- Physics Today 16, (Jan 1963), pg. 30.
 A nice analogy is Figure-Ground studies such as the one shown to the right. Looked at one way, it is a drawing of a vase; looked at another way it is two faces.
A nice analogy is Figure-Ground studies such as the one shown to the right. Looked at one way, it is a drawing of a vase; looked at another way it is two faces.
We can switch back and forth between the two viewpoints. But we can not see both at once. But the figure is both at once.
Similarly, we can think of an electron as a wave or we can think of an electron as a particle, but we can not think of it as both at once. But in some sense the electron is both at once. Being able to think of these two viewpoints at once is in some sense being able to understand Quantum Mechanics.
I do not believe that Quantum Mechanics is understandable, at least for the usual meaning of the word understand.
Thus when we think of an electron in a Hydrogen atom, we can imagine it as a particle in orbit around the central proton. We can also imagine it as the wave function, its wave aspect; it turns out that the wave function for the electron in the Hydrogen atom is spherically symmetric with maximum density at the center of the atom.
![]() A Flash animation of these two viewpoints of an electron in a Hydrogen atom may be accessed by clicking on the red button to the right. It will appear in a separate window, and has a file size of 9.6k In order to view it, you need to have the Flash player of Version 5 or later installed on your computer; the Flash player is available free fromhttp://www.macromedia.com/
A Flash animation of these two viewpoints of an electron in a Hydrogen atom may be accessed by clicking on the red button to the right. It will appear in a separate window, and has a file size of 9.6k In order to view it, you need to have the Flash player of Version 5 or later installed on your computer; the Flash player is available free fromhttp://www.macromedia.com/
We can illustrate the Principle of Complementarity with some examples by Bohr himself:
- "The opposite of a true statement is a false statement, but the opposite of a profound truth is usually another profound truth."
- Life: a form through which matter streams.
Life: a collection of matter. - Justice and love.
References to the above examples are:
- Ken Wilbur, Spectrum of Consciousness, pg. 34.
- Heisenberg, Physics and Beyond, pg. 105.
- From the Chinese Taoist text I Ching, as reported in Reference 2, pg. 15.
 In 1947 Bohr was awarded the Order of the Elephant from the Danish government. For a proud Dane like Bohr, this was a very big deal, and Bohr is the only person to be awarded it who was not royalty and/or a famous general. As part of the award, the winner's family coat of arms is carved into a sort of wall of fame. Bohr's family, though, did not have a coat of arms, so Bohr got to design one himself. The figure to the right is what he designed.
In 1947 Bohr was awarded the Order of the Elephant from the Danish government. For a proud Dane like Bohr, this was a very big deal, and Bohr is the only person to be awarded it who was not royalty and/or a famous general. As part of the award, the winner's family coat of arms is carved into a sort of wall of fame. Bohr's family, though, did not have a coat of arms, so Bohr got to design one himself. The figure to the right is what he designed.
You will notice that he choose the ancient Chinese symbol for the Tao, the "Yin-Yang Symbol," for the centerpiece. He did not do this lightly. The inscription reads CONTRARI SUNT COMPLEMENTA or Opposites Are Complements. Thus he chose to represent his Principle of Complementarity as the centrepiece of his coat of arms.
As you probably know, in Taoist philosophy all is related to pairs of opposites which are called Yang and Yin. The table below illustrates. All the entries but the last are as given by the traditional Taoist classification.
| Yang | Yin |
|---|---|
| Sunny | Shady |
| Masculine | Feminine |
| Active | Passive |
| Rational | Intuitive |
| Heavy | Light |
| Particle | Wave |
The last entry in the above table is by the author of this document. You may wish to muse about whether I have got the right label in the correct column.
Similarly, the first two of the following quotations are famous to Taoists, while the last is not nearly as well-known:
- "The ten thousand things carry yin and embrace yang.
They achieve harmony by combining these forces."
-- Lao Tsu, Tao Te Ching 42 - "The Tao that can be told is not the true Tao."
-- Tao Te Ching 1 - "The electron that can be told is not the true electron."
-- David Harrison
At the risk of pushing the illustration of Western physics by means of Eastern ideas too far, you may wish to consider the following:
"[In 1961] I had occasion to discuss Bohr's ideas with the great Japanese physicist [Yukawa], whose conception of the meson with its complementary aspects of elementary particle and field of nuclear force is one of the most striking illustrations of the fruitfulness of the new way of looking at things that we owe to Neils Bohr. I asked Yukawa whether the Japanese physicists had the same difficulty as their Western colleagues in assimilating the idea of complementarity ... He answered `No, Bohr's argumentation has always appeared quite evident to us; ... you see, we in Japan have not been corrupted by Aristotle." -- Rosenfeld, Physics Today 16, (Oct 1963), pg. 47.
Finally, we close this section by considering the methodology used by Bohr, as well as many other creative geniuses both in and out of the sciences: paradox.
"Among all paradigms for probing a puzzle, physics proffers none with more promise than a paradox ... No one took the paradox [of quantum theory] more seriously than Bohr. No one worked around the central mystery with more energy wherever work was possible. No one brought to bear a more judicious combination of daring and conservativeness, nor a deeper feel for the harmony of physics." -- Misner, Thorne, and Wheeler, Gravitation pg. 1197
"The Copenhagen interpretation of quantum theory starts from a paradox." Heisenberg, Physics and Philosophy, pg. 44.
Similarly, in the Eastern traditions understanding is often achieved through deep consideration of paradox. A well-known example is the koans used in the Zen tradition. A famous koan is "What is the sound of one hand clapping?" There are more-or-less unique correct answers to the koans, which can be found by deep internal questioning.
Copenhagen Interpretation of Quantum Mechanics
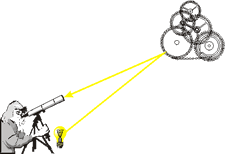 If the Complementarity Principle is subtle, complex, and difficult to understand, then its extension into Bohr's interpretation of Quantum Mechanics will share these characteristics with some added subtlety. We begin by considering an apparatus making a measurement on some system:
If the Complementarity Principle is subtle, complex, and difficult to understand, then its extension into Bohr's interpretation of Quantum Mechanics will share these characteristics with some added subtlety. We begin by considering an apparatus making a measurement on some system:
The apparatus consists of a light source and a detector, which is the telescope and observer. The apparatus is making measurements on a system which in this example consists of some gears. The light source emits photons, the particulate aspect of light. The photons are "reflected" by the system, and enter the detector. The reflection of the photons off the gears necessarily disturbs the system we are attempting to measure.
If we attempt to reduce the disturbance on the system due to our measurements on it, we eventually reach a point where we have reached an irreducible minimum: this is when the interaction involves the exchange of a single quantum of energy, emitted by the light source, reflected off the system, and detected by the telescope and observer
The situation is actually even more complex than this. In fact, the photon from the light bulb is absorbed by the gears, which then emits another photon which ends up in the detector. If the "observer" were some sort of detector capable of detecting a single photon that would be the end of the story. But for the human observer shown, that single photon would have to enter his eye, be absorbed by the retina, which in turn causes an electrical impulse to go up the optic nerve to the brain where in principle the brain would process it; for real humans the minimum light level that is perceptible corresponds to a few photons, not a single one. So for a human to participate in this minimal observation, we would require a detector capable of registering a single photon and sending a larger signal, such as a flashing light, which a human can perceive.
The fact that the interaction cannot be reduced beyond a minimum amount, the interchange of a single photon, is the heart of the Heisenberg Uncertainty Principle. However, Bohr realised that it means even more than this. At this level we can not divide the quantum of energy into a contribution from the apparatus and a contribution from the system: the process is inseparable. Thus it is holistic.
This in turn means that at this level it is not meaningful to talk about the system at all separate from the apparatus observing it. As Bohr repeatedly said, "The quantum world does not exist."
Wheeler made a similar conclusion when he suggested that we should drop the word observer from our vocabulary, replacing it with the word participator.
In fact, the separation between the observer and the observed is always more-or-less arbitrary, although we customarily ignore that fact. An example by Bohr may clarify:
We customarily think of the outside world as separate from ourselves, and the boundary between the two is the surface of our skin. However, think of a blind person who gets around with the assistance of a cane. In time that person will probably treat the cane as part of his or her body, and will think of the outside world as beginning just at the tip of the cane. Now imagine the blind man's sense of touch extending out of the tip of the cane and into the roadway itself. Imagine it extending further, down the block, into the countryside, to the whole world. There is no point where the blind man ends and the world begins. Similarly, we can not say which is the system and which is us observing it.
This is the heart of the Copenhagen Interpretation of Quantum Mechanics.
We conclude this section with a further subtlety. The energy of a photon, the particulate aspect of light, is related to the wavelength of the wave aspect of the same light. We can reduce the energy of an individual photon by increasing the wavelength. Thus, we can reduce the disturbance on the system we are attempting to observe by using light of a larger wavelength. However, our ability to see the details of an object also depends on the wavelength of the light: we can not see details that are smaller than the wavelength. In the usual case we don't notice this because the wavelength of visible light is so small compared to everyday distances.
However, in the case of a quantum measurement we are typically investigating systems that are very small. Thus there is a meaningful maximum wavelength for the light we are using if we wish to see the system. So the minimum interaction between the apparatus and the system involves a single photon with a maximum wavelength, i.e. a single photon with a minimum energy. This minimum energy of the photon further constrains the minimum amount of disturbance we introduce by doing a measurement.
Technical note: the energy of the photon equals h c / wavelength, where h is Planck's constant and c is the speed of light.
Author
This document was written by David M. Harrison, Dept. of Physics, University of Toronto, harrison@physics.utoronto.ca in March 2000. This is version 1.6, date (m/d/y) 03/27/06.

