4.8: Selected Examples

\( \newcommand\bes{\begin{equation}\begin{split}}\)
\( \newcommand\ltwid{\propto}\)
\( \newcommand\ees{\end{split}\end{equation}}\)
\( \newcommand\mib{\mathbf}\)
\( \newcommand\Sa{\textsf a}\)
\( \newcommand\Sb{\textsf b}\)
\( \newcommand\Sc{\textsf c}\)
\( \newcommand\Sd{\textsf d}\)
\( \newcommand\Se{\textsf e}\)
\( \newcommand\Sf{\textsf f}\)
\( \newcommand\Sg{\textsf g}\)
\( \newcommand\Sh{\textsf h}\)
\( \newcommand\Si{\textsf i}\)
\( \newcommand\Sj{\textsf j}\)
\( \newcommand\Sk{\textsf k}\)
\( \newcommand\Sl{\textsf l}\)
\( \newcommand\Sm{\textsf m}\)
\( \newcommand\Sn{\textsf n}\)
\( \newcommand\So{\textsf o}\)
\( \newcommand\Sp{\textsf p}\)
\( \newcommand\Sq{\textsf q}\)
\( \newcommand\Sr{\textsf r}\)
\( \newcommand\Ss{\textsf s}\)
\( \newcommand\St{\textsf t}\)
\( \newcommand\Su{\textsf u}\)
\( \newcommand\Sv{\textsf v}\)
\( \newcommand\Sw{\textsf w}\)
\( \newcommand\Sx{\textsf x}\)
\( \newcommand\Sy{\textsf y}\)
\( \newcommand\Sz{\textsf z}\)
\( \newcommand\SA{\textsf A}\)
\( \newcommand\SB{\textsf B}\)
\( \newcommand\SC{\textsf C}\)
\( \newcommand\SD{\textsf D}\)
\( \newcommand\SE{\textsf E}\)
\( \newcommand\SF{\textsf F}\)
\( \newcommand\SG{\textsf G}\)
\( \newcommand\SH{\textsf H}\)
\( \newcommand\SI{\textsf I}\)
\( \newcommand\SJ{\textsf J}\)
\( \newcommand\SK{\textsf K}\)
\( \newcommand\SL{\textsf L}\)
\( \newcommand\SM{\textsf M}\)
\( \newcommand\SN{\textsf N}\)
\( \newcommand\SO{\textsf O}\)
\( \newcommand\SP{\textsf P}\)
\( \newcommand\SQ{\textsf Q}\)
\( \newcommand\SR{\textsf R}\)
\( \newcommand\SS{\textsf S}\)
\( \newcommand\ST{\textsf T}\)
\( \newcommand\SU{\textsf U}\)
\( \newcommand\SV{\textsf V}\)
\( \newcommand\SW{\textsf W}\)
\( \newcommand\SX{\textsf X}\)
\( \newcommand\SY{\textsf Y}\)
\( \newcommand\SZ{\textsf Z}\)
\( \newcommand\Ha{\hat a}\)
\( \newcommand\Hb{\hat b}\)
\( \newcommand\Hc{\hat c}\)
\( \newcommand\Hd{\hat d}\)
\( \newcommand\He{\hat e}\)
\( \newcommand\Hf{\hat f}\)
\( \newcommand\Hg{\hat g}\)
\( \newcommand\Hh{\hat h}\)
\( \newcommand\Hi{\hat \imath}\)
\( \newcommand\Hj{\hat \jmath}\)
\( \newcommand\Hk{\hat k}\)
\( \newcommand\Hl{\hat l}\)
\( \newcommand\Hm{\hat m}\)
\( \newcommand\Hn{\hat n}\)
\( \newcommand\Ho{\hat o}\)
\( \newcommand\Hp{\hat p}\)
\( \newcommand\Hq{\hat q}\)
\( \newcommand\Hr{\hat r}\)
\( \newcommand\Hs{\hat s}\)
\( \newcommand\Ht{\hat t}\)
\( \newcommand\Hu{\hat u}\)
\( \newcommand\Hv{\hat v}\)
\( \newcommand\Hw{\hat w}\)
\( \newcommand\Hx{\hat x}\)
\( \newcommand\Hy{\hat y}\)
\( \newcommand\Hz{\hat z}\)
\( \newcommand\HA{\hat A}\)
\( \newcommand\HB{\hat B}\)
\( \newcommand\HC{\hat C}\)
\( \newcommand\HD{\hat D}\)
\( \newcommand\HE{\hat E}\)
\( \newcommand\HF{\hat F}\)
\( \newcommand\HG{\hat G}\)
\( \newcommand\HH{\hat H}\)
\( \newcommand\HI{\hat I}\)
\( \newcommand\HJ{\hat J}\)
\( \newcommand\HK{\hat K}\)
\( \newcommand\HL{\hat L}\)
\( \newcommand\HM{\hat M}\)
\( \newcommand\HN{\hat N}\)
\( \newcommand\HO{\hat O}\)
\( \newcommand\HP{\hat P}\)
\( \newcommand\HQ{\hat Q}\)
\( \newcommand\HR{\hat R}\)
\( \newcommand\HS{\hat S}\)
\( \newcommand\HT{\hat T}\)
\( \newcommand\HU{\hat U}\)
\( \newcommand\HV{\hat V}\)
\( \newcommand\HW{\hat W}\)
\( \newcommand\HX{\hat X}\)
\( \newcommand\HY{\hat Y}\)
\( \newcommand\HZ{\hat Z}\)
\( \newcommand\Halpha{\hat\alpha}\)
\( \newcommand\Hbeta{\hat\beta}\)
\( \newcommand\Hgamma{\hat\gamma}\)
\( \newcommand\Hdelta{\hat\delta}\)
\( \newcommand\Hepsilon{\hat\epsilon}\)
\( \newcommand\Hvarepsilon{\hat\varepsilon}\)
\( \newcommand\Hzeta{\hat\zeta}\)
\( \newcommand\Heta{\hat\eta}\)
\( \newcommand\Htheta{\hat\theta}\)
\( \newcommand\Hvartheta{\hat\vartheta}\)
\( \newcommand\Hiota{\hat\iota}\)
\( \newcommand\Hkappa{\hat\kappa}\)
\( \newcommand\Hlambda{\hat\lambda}\)
\( \newcommand\Hmu{\hat\mu}\)
\( \newcommand\Hnu{\hat\nu}\)
\( \newcommand\Hxi{\hat\xi}\)
\( \newcommand\Hom{\hat\omicron}\)
\( \newcommand\Hpi{\hat\pi}\)
\( \newcommand\Hvarpi{\hat\varpi}\)
\( \newcommand\Hrho{\hat\rho}\)
\( \newcommand\Hvarrho{\hat\varrho}\)
\( \newcommand\Hsigma{\hat\sigma}\)
\( \newcommand\Hvarsigma{\hat\varsigma}\)
\( \newcommand\Htau{\var\tau}\)
\( \newcommand\Hupsilon{\hat\upsilon}\)
\( \newcommand\Hphi{\hat\phi}\)
\( \newcommand\Hvarphi{\hat\varphi}\)
\( \newcommand\Hchi{\hat\chi}\)
\( \newcommand\Hxhi{\hat\xhi}\)
\( \newcommand\Hpsi{\hat\psi}\)
\( \newcommand\Homega{\hat\omega}\)
\( \newcommand\HGamma{\hat\Gamma}\)
\( \newcommand\HDelta{\hat\Delta}\)
\( \newcommand\HTheta{\hat\Theta}\)
\( \newcommand\HLambda{\hat\Lambda}\)
\( \newcommand\HXi{\hat\Xi}\)
\( \newcommand\HPi{\hat\Pi}\)
\( \newcommand\HSigma{\hat\Sigma}\)
\( \newcommand\HUps{\hat\Upsilon}\)
\( \newcommand\HPhi{\hat\Phi}\)
\( \newcommand\HPsi{\hat\Psi}\)
\( \newcommand\HOmega{\hat\Omega}\)
\( \newcommand\xhat{\hat\Bx}\)
\( \newcommand\yhat{\hat\By}\)
\( \newcommand\zhat{\hat\Bz}\)
\( \newcommand\ehat{\hat\Be}\)
\( \newcommand\khat{\hat\Bk}\)
\( \newcommand\nhat{\hat\Bn}\)
\( \newcommand\rhat{\hat\Br}\)
\( \newcommand\phihat{\hat\Bphi}\)
\( \newcommand\thetahat{\hat\Btheta}\)
\( \newcommand\MA{\mathbb A}\)
\( \newcommand\MB{\mathbb B}\)
\( \newcommand\MC{\mathbb C}\)
\( \newcommand\MD{\mathbb D}\)
\( \newcommand\ME{\mathbb E}\)
\( \newcommand\MF{\mathbb F}\)
\( \newcommand\MG{\mathbb G}\)
\( \newcommand\MH{\mathbb H}\)
\( \newcommand\MI{\mathbb I}\)
\( \newcommand\MJ{\mathbb J}\)
\( \newcommand\MK{\mathbb K}\)
\( \newcommand\ML{\mathbb L}\)
\( \newcommand\MM{\mathbb M}\)
\( \newcommand\MN{\mathbb N}\)
\( \newcommand\MO{\mathbb O}\)
\( \newcommand\MP{\mathbb P}\)
\( \newcommand\MQ{\mathbb Q}\)
\( \newcommand\MR{\mathbb R}\)
\( \newcommand\MS{\mathbb S}\)
\( \newcommand\MT{\mathbb T}\)
\( \newcommand\MU{\mathbb U}\)
\( \newcommand\MV{\mathbb V}\)
\( \newcommand\MW{\mathbb W}\)
\( \newcommand\MX{\mathbb X}\)
\( \newcommand\MY{\mathbb Y}\)
\( \newcommand\MZ{\mathbb Z}\)
\( \newcommand\CA{\mathcal A}\)
\( \newcommand\CB{\mathcal B}\)
\( \newcommand\CC{\mathcal C}\)
\( \newcommand\CD{\mathcal D}\)
\( \newcommand\CE{\mathcal E}\)
\( \newcommand\CF{\mathcal F}\)
\( \newcommand\CG{\mathcal G}\)
\( \newcommand\CH{\mathcal H}\)
\( \newcommand\CI{\mathcal I}\)
\( \newcommand\CJ{\mathcal J}\)
\( \newcommand\CK{\mathcal K}\)
\( \newcommand\CL{\mathcal L}\)
\( \newcommand\CM{\mathcal M}\)
\( \newcommand\CN{\mathcal N}\)
\( \newcommand\CO{\mathcal O}\)
\( \newcommand\CP{\mathcal P}\)
\( \newcommand\CQ{\mathcal Q}\)
\( \newcommand\CR{\mathcal R}\)
\( \newcommand\CS{\mathcal S}\)
\( \newcommand\CT{\mathcal T}\)
\( \newcommand\CU{\mathcal U}\)
\( \newcommand\CV{\mathcal V}\)
\( \newcommand\CW{\mathcal W}\)
\( \newcommand\CX{\mathcal X}\)
\( \newcommand\CY{\mathcal Y}\)
\( \newcommand\CZ{\mathcal Z}\)
\( \newcommand\Fa{\mathfrak a}\)
\( \newcommand\Fb{\mathfrak b}\)
\( \newcommand\Fc{\mathfrak c}\)
\( \newcommand\Fd{\mathfrak d}\)
\( \newcommand\Fe{\mathfrak e}\)
\( \newcommand\Ff{\mathfrak f}\)
\( \newcommand\Fg{\mathfrak g}\)
\( \newcommand\Fh{\mathfrak h}\)
\( \newcommand\Fi{\mathfrak i}\)
\( \newcommand\Fj{\mathfrak j}\)
\( \newcommand\Fk{\mathfrak k}\)
\( \newcommand\Fl{\mathfrak l}\)
\( \newcommand\Fm{\mathfrak m}\)
\( \newcommand\Fn{\mathfrak n}\)
\( \newcommand\Fo{\mathfrak o}\)
\( \newcommand\Fp{\mathfrak p}\)
\( \newcommand\Fq{\mathfrak q}\)
\( \newcommand\Fr{\mathfrak r}\)
\( \newcommand\Fs{\mathfrak s}\)
\( \newcommand\Ft{\mathfrak t}\)
\( \newcommand\Fu{\mathfrak u}\)
\( \newcommand\Fv{\mathfrak v}\)
\( \newcommand\Fw{\mathfrak w}\)
\( \newcommand\Fx{\mathfrak x}\)
\( \newcommand\Fy{\mathfrak y}\)
\( \newcommand\Fz{\mathfrak z}\)
\( \newcommand\FA{\mathfrak A}\)
\( \newcommand\FB{\mathfrak B}\)
\( \newcommand\FC{\mathfrak C}\)
\( \newcommand\FD{\mathfrak D}\)
\( \newcommand\FE{\mathfrak E}\)
\( \newcommand\FF{\mathfrak F}\)
\( \newcommand\FG{\mathfrak G}\)
\( \newcommand\FH{\mathfrak H}\)
\( \newcommand\FI{\mathfrak I}\)
\( \newcommand\FJ{\mathfrak J}\)
\( \newcommand\FK{\mathfrak K}\)
\( \newcommand\FL{\mathfrak L}\)
\( \newcommand\FM{\mathfrak M}\)
\( \newcommand\FN{\mathfrak N}\)
\( \newcommand\FO{\mathfrak O}\)
\( \newcommand\FP{\mathfrak P}\)
\( \newcommand\FQ{\mathfrak Q}\)
\( \newcommand\FR{\mathfrak R}\)
\( \newcommand\FS{\mathfrak S}\)
\( \newcommand\FT{\mathfrak T}\)
\( \newcommand\FU{\mathfrak U}\)
\( \newcommand\FV{\mathfrak V}\)
\( \newcommand\FW{\mathfrak W}\)
\( \newcommand\FX{\mathfrak X}\)
\( \newcommand\FY{\mathfrak Y}\)
\( \newcommand\FZ{\mathfrak Z}\)
\( \newcommand\Da{\dot a}\)
\( \newcommand\Db{\dot b}\)
\( \newcommand\Dc{\dot c}\)
\( \newcommand\Dd{\dot d}\)
\( \newcommand\De{\dot e}\)
\( \newcommand\Df{\dot f}\)
\( \newcommand\Dg{\dot g}\)
\( \newcommand\Dh{\dot h}\)
\( \newcommand\Di{\dot \imath}\)
\( \newcommand\Dj{\dot \jmath}\)
\( \newcommand\Dk{\dot k}\)
\( \newcommand\Dl{\dot l}\)
\( \newcommand\Dm{\dot m}\)
\( \newcommand\Dn{\dot n}\)
\( \newcommand\Do{\dot o}\)
\( \newcommand\Dp{\dot p}\)
\( \newcommand\Dq{\dot q}\)
\( \newcommand\Dr{\dot r}\)
\( \newcommand\Ds{\dot s}\)
\( \newcommand\Dt{\dot t}\)
\( \newcommand\Du{\dot u}\)
\( \newcommand\Dv{\dot v}\)
\( \newcommand\Dw{\dot w}\)
\( \newcommand\Dx{\dot x}\)
\( \newcommand\Dy{\dot y}\)
\( \newcommand\Dz{\dot z}\)
\( \newcommand\DA{\dot A}\)
\( \newcommand\DB{\dot B}\)
\( \newcommand\DC{\dot C}\)
\( \newcommand\DD{\dot D}\)
\( \newcommand\DE{\dot E}\)
\( \newcommand\DF{\dot F}\)
\( \newcommand\DG{\dot G}\)
\( \newcommand\DH{\dot H}\)
\( \newcommand\DI{\dot I}\)
\( \newcommand\DJ{\dot J}\)
\( \newcommand\DK{\dot K}\)
\( \newcommand\DL{\dot L}\)
\( \newcommand\DM{\dot M}\)
\( \newcommand\DN{\dot N}\)
\( \newcommand\DO{\dot O}\)
\( \newcommand\DP{\dot P}\)
\( \newcommand\DQ{\dot Q}\)
\( \newcommand\DR{\dot R}\)
\( \newcommand\DS{\dot S}\)
\( \newcommand\DT{\dot T}\)
\( \newcommand\DU{\dot U}\)
\( \newcommand\DV{\dot V}\)
\( \newcommand\DW{\dot W}\)
\( \newcommand\DX{\dot X}\)
\( \newcommand\DY{\dot Y}\)
\( \newcommand\DZ{\dot Z}\)
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dmu{\dot\mu}\)
\( \newcommand\Dnu{\dot\nu}\)
\( \newcommand\Dxi{\dot\xi}\)
\( \newcommand\Dom{\dot\omicron}\)
\( \newcommand\Dpi{\dot\pi}\)
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Drho{\dot\rho}\)
\( \newcommand\Dvarrho{\dot\varrho}\)
\( \newcommand\Dsigma{\dot\sigma}\)
\( \newcommand\Dvarsigma{\dot\varsigma}\)
\( \newcommand\Dtau{\var\tau}\)
\( \newcommand\Dupsilon{\dot\upsilon}\)
\( \newcommand\Dphi{\dot\phi}\)
\( \newcommand\Dvarphi{\dot\varphi}\)
\( \newcommand\Dchi{\dot\chi}\)
\( \newcommand\Dpsi{\dot\psi}\)
\( \newcommand\Domega{\dot\omega}\)
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DLambda{\dot\Lambda}\)
\( \newcommand\DXi{\dot\Xi}\)
\( \newcommand\DPi{\dot\Pi}\)
\( \newcommand\DSigma{\dot\Sigma}\)
\( \newcommand\DUps{\dot\Upsilon}\)
\( \newcommand\DPhi{\dot\Phi}\)
\( \newcommand\DPsi{\dot\Psi}\)
\( \newcommand\DOmega{\dot\Omega}\)
\( \newcommand\Va{\vec a}\)
\( \newcommand\Vb{\vec b}\)
\( \newcommand\Vc{\vec c}\)
\( \newcommand\Vd{\vec d}\)
\( \newcommand\Ve{\vec e}\)
\( \newcommand\Vf{\vec f}\)
\( \newcommand\Vg{\vec g}\)
\( \newcommand\Vh{\vec h}\)
\( \newcommand\Vi{\vec \imath}\)
\( \newcommand\Vj{\vec \jmath}\)
\( \newcommand\Vk{\vec k}\)
\( \newcommand\Vl{\vec l}\)
\( \newcommand\Vm{\vec m}\)
\( \newcommand\Vn{\vec n}\)
\( \newcommand\Vo{\vec o}\)
\( \newcommand\Vp{\vec p}\)
\( \newcommand\Vq{\vec q}\)
\( \newcommand\Vr{\vec r}\)
\( \newcommand\Vs{\vec s}\)
\( \newcommand\Vt{\vec t}\)
\( \newcommand\Vu{\vec u}\)
\( \newcommand\Vv{\vec v}\)
\( \newcommand\Vw{\vec w}\)
\( \newcommand\Vx{\vec x}\)
\( \newcommand\Vy{\vec y}\)
\( \newcommand\Vz{\vec z}\)
\( \newcommand\VA{\vec A}\)
\( \newcommand\VB{\vec B}\)
\( \newcommand\VC{\vec C}\)
\( \newcommand\VD{\vec D}\)
\( \newcommand\VE{\vec E}\)
\( \newcommand\VF{\vec F}\)
\( \newcommand\VG{\vec G}\)
\( \newcommand\VH{\vec H}\)
\( \newcommand\VI{\vec I}\)
\( \newcommand\VJ{\vec J}\)
\( \newcommand\VK{\vec K}\)
\( \newcommand\VL{\vec L}\)
\( \newcommand\VM{\vec M}\)
\( \newcommand\VN{\vec N}\)
\( \newcommand\VO{\vec O}\)
\( \newcommand\VP{\vec P}\)
\( \newcommand\VQ{\vec Q}\)
\( \newcommand\VR{\vec R}\)
\( \newcommand\VS{\vec S}\)
\( \newcommand\VT{\vec T}\)
\( \newcommand\VU{\vec U}\)
\( \newcommand\VV{\vec V}\)
\( \newcommand\VW{\vec W}\)
\( \newcommand\VX{\vec X}\)
\( \newcommand\VY{\vec Y}\)
\( \newcommand\VZ{\vec Z}\)
\( \newcommand\Valpha{\vec\alpha}\)
\( \newcommand\Vbeta{\vec\beta}\)
\( \newcommand\Vgamma{\vec\gamma}\)
\( \newcommand\Vdelta{\vec\delta}\)
\( \newcommand\Vepsilon{\vec\epsilon}\)
\( \newcommand\Vvarepsilon{\vec\varepsilon}\)
\( \newcommand\Vzeta{\vec\zeta}\)
\( \newcommand\Veta{\vec\eta}\)
\( \newcommand\Vtheta{\vec\theta}\)
\( \newcommand\Vvartheta{\vec\vartheta}\)
\( \newcommand\Viota{\vec\iota}\)
\( \newcommand\Vkappa{\vec\kappa}\)
\( \newcommand\Vlambda{\vec\lambda}\)
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VTheta{\vec\Theta}\)
\( \newcommand\VLambda{\vec\Lambda}\)
\( \newcommand\VXi{\vec\Xi}\)
\( \newcommand\VPi{\vec\Pi}\)
\( \newcommand\VSigma{\vec\Sigma}\)
\( \newcommand\VUps{\vec\Upsilon}\)
\( \newcommand\VPhi{\vec\Phi}\)
\( \newcommand\VPsi{\vec\Psi}\)
\( \newcommand\VOmega{\vec\Omega}\)
\( \newcommand\BA{\mib A}\)
\( \newcommand\BB{\mib B}\)
\( \newcommand\BC{\mib C}\)
\( \newcommand\BD{\mib D}\)
\( \newcommand\BE{\mib E}\)
\( \newcommand\BF{\mib F}\)
\( \newcommand\BG{\mib G}\)
\( \newcommand\BH{\mib H}\)
\( \newcommand\BI{\mib I}}\)
\( \newcommand\BJ{\mib J}\)
\( \newcommand\BK{\mib K}\)
\( \newcommand\BL{\mib L}\)
\( \newcommand\BM{\mib M}\)
\( \newcommand\BN{\mib N}\)
\( \newcommand\BO{\mib O}\)
\( \newcommand\BP{\mib P}\)
\( \newcommand\BQ{\mib Q}\)
\( \newcommand\BR{\mib R}\)
\( \newcommand\BS{\mib S}\)
\( \newcommand\BT{\mib T}\)
\( \newcommand\BU{\mib U}\)
\( \newcommand\BV{\mib V}\)
\( \newcommand\BW{\mib W}\)
\( \newcommand\BX{\mib X}\)
\( \newcommand\BY{\mib Y}\)
\( \newcommand\BZ{\mib Z}\)
\( \newcommand\Ba{\mib a}\)
\( \newcommand\Bb{\mib b}\)
\( \newcommand\Bc{\mib c}\)
\( \newcommand\Bd{\mib d}\)
\( \newcommand\Be{\mib e}\)
\( \newcommand\Bf{\mib f}\)
\( \newcommand\Bg{\mib g}\)
\( \newcommand\Bh{\mib h}\)
\( \newcommand\Bi{\mib i}\)
\( \newcommand\Bj{\mib j}\)
\( \newcommand\Bk{\mib k}\)
\( \newcommand\Bl{\mib l}\)
\( \newcommand\Bm{\mib m}\)
\( \newcommand\Bn{\mib n}\)
\( \newcommand\Bo{\mib o}\)
\( \newcommand\Bp{\mib p}\)
\( \newcommand\Bq{\mib q}\)
\( \newcommand\Br{\mib r}\)
\( \newcommand\Bs{\mib s}\)
\( \newcommand\Bt{\mib t}\)
\( \newcommand\Bu{\mib u}\)
\( \newcommand\Bv{\mib v}\)
\( \newcommand\Bw{\mib w}\)
\( \newcommand\Bx{\mib x}\)
\( \newcommand\By{\mib y}\)
\( \newcommand\Bz{\mib z}\)\)
\( \newcommand\vrh{\varrho}\)
\( \newcommand\vsig{\varsigma}\)
\( \newcommand\ups{\upsilon}\)
\( \newcommand\eps{\epsilon}\)
\( \newcommand\ve{\varepsilon}\)
\( \newcommand\vth{\vartheta}\)
\( \newcommand\vphi{\varphi}\)
\( \newcommand\xhi{\chi}\)
\( \newcommand\Ups{\Upsilon}\)
\( \newcommand\Balpha{\mib\alpha}\)
\( \newcommand\Bbeta{\mib\beta}\)
\( \newcommand\Bgamma{\mib\gamma}\)
\( \newcommand\Bdelta{\mib\delta}\)
\( \newcommand\Beps{\mib\epsilon}\)
\( \newcommand\Bve{\mib\varepsilon}\)
\( \newcommand\Bzeta{\mib\zeta}\)
\( \newcommand\Beta{\mib\eta}\)
\( \newcommand\Btheta{\mib\theta}\)
\( \newcommand\Bvth{\mib\vartheta}\)
\( \newcommand\Biota{\mib\iota}\)
\( \newcommand\Bkappa{\mib\kappa}\)
\( \newcommand\Blambda{\mib\lambda}\)
\( \newcommand\Bmu{\mib\mu}\)
\( \newcommand\Bnu{\mib\nu}\)
\( \newcommand\Bxi{\mib\xi}\)
\( \newcommand\Bom{\mib\omicron}\)
\( \newcommand\Bpi{\mib\pi}\)
\( \newcommand\Bvarpi{\mib\varpi}\)
\( \newcommand\Brho{\mib\rho}\)
\( \newcommand\Bvrh{\mib\varrho}\)
\( \newcommand\Bsigma{\mib\sigma}\)
\( \newcommand\Bvsig{\mib\varsigma}\)
\( \newcommand\Btau{\mib\tau}\)
\( \newcommand\Bups{\mib\upsilon}\)
\( \newcommand\Bphi{\mib\phi}\)
\( \newcommand\Bvphi{\mib\vphi}\)
\( \newcommand\Bchi{\mib\chi}\)
\( \newcommand\Bpsi{\mib\psi}\)
\( \newcommand\Bomega{\mib\omega}\)
\( \newcommand\BGamma{\mib\Gamma}\)
\( \newcommand\BDelta{\mib\Delta}\)
\( \newcommand\BTheta{\mib\Theta}\)
\( \newcommand\BLambda{\mib\Lambda}\)
\( \newcommand\BXi{\mib\Xi}\)
\( \newcommand\BPi{\mib\Pi}\)
\( \newcommand\BSigma{\mib\Sigma}\)
\( \newcommand\BUps{\mib\Upsilon}\)
\( \newcommand\BPhi{\mib\Phi}\)
\( \newcommand\BPsi{\mib\Psi}\)
\( \newcommand\BOmega{\mib\Omega}\)
\( \newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}\)
\( \newcommand\RGamma{ \Gamma}\)
\( \newcommand\RDelta{ \Delta}\)
\( \newcommand\RTheta{ \Theta}\)
\( \newcommand\RLambda{ \Lambda}\)
\( \newcommand\RXi{ \Xi}\)
\( \newcommand\RPi{ \Pi}\)
\( \newcommand\RSigma{ \Sigma}\)
\( \newcommand\RUps{ \Upsilon}\)
\( \newcommand\RPhi{ \Phi}\)
\( \newcommand\RPsi{ \Psi}\)
\( \newcommand\ROmega{ \Omega}\)
\( \newcommand\RA{ A}\)
\( \newcommand\RB{ B}\)
\( \newcommand\RC{ C}\)
\( \newcommand\RD{ D}\)
\( \newcommand\RE{ E}\)
\( \newcommand\RF{ F}\)
\( \newcommand\RG{ G}\)
\( \newcommand\RH{ H}\)
\( \newcommand\RI{ I}\)
\( \newcommand\RJ{ J}\)
\( \newcommand\RK{ K}\)
\( \newcommand\RL{ L}\)
\( \newcommand { M}\)
\( \newcommand\RN{ N}\)
\( \newcommand\RO{ O}\)
\( \newcommand\RP{ P}\)
\( \newcommand\RQ{ Q}\)
\( \newcommand\RR{ R}\)
\( \newcommand\RS{ S}\)
\( \newcommand\RT{ T}\)
\( \newcommand\RU{ U}\)
\( \newcommand\RV{ V}\)
\( \newcommand\RW{ W}\)
\( \newcommand\RX{ X}\)
\( \newcommand\RY{ Y}\)
\( \newcommand\RZ{ Z}\)
\( \newcommand\Ra{ a}\)
\( \newcommand\Rb{ b}\)
\( \newcommand\Rc{ c}\)
\( \newcommand\Rd{ d}\)
\( \newcommand\Re{ e}\)
\( \newcommand\Rf{ f}\)
\( \newcommand\Rg{ g}\)
\( \newcommand\Rh{ h}\)
\( \newcommand\Ri{ i}\)
\( \newcommand\Rj{ j}\)
\( \newcommand\Rk{ k}\)
\( \newcommand\Rl{ l}\)
\( \newcommand { m}\)
\( \newcommand\Rn{ n}\)
\( \newcommand\Ro{ o}\)
\( \newcommand\Rp{ p}\)
\( \newcommand\Rq{ q}\)
\( \newcommand\Rr{ r}\)
\( \newcommand\Rs{ s}\)
\( \newcommand\Rt{ t}\)
\( \newcommand\Ru{ u}\)
\( \newcommand\Rv{ v}\)
\( \newcommand\Rw{ w}\)
\( \newcommand\Rx{ x}\)
\( \newcommand\Ry{ y}\)
\( \newcommand\Rz{ z}\)
\( \newcommand\BBA{\boldsymbol\RA}\)
\( \newcommand\BBB{\boldsymbol\RB}\)
\( \newcommand\BBC{\boldsymbol\RC}\)
\( \newcommand\BBD{\boldsymbol\RD}\)
\( \newcommand\BBE{\boldsymbol\RE}\)
\( \newcommand\BBF{\boldsymbol\RF}\)
\( \newcommand\BBG{\boldsymbol\RG}\)
\( \newcommand\BBH{\boldsymbol\RH}\)
\( \newcommand\BBI{\boldsymbol\RI}\)
\( \newcommand\BBJ{\boldsymbol\RJ}\)
\( \newcommand\BBK{\boldsymbol\RK}\)
\( \newcommand\BBL{\boldsymbol\RL}\)
\( \newcommand\BBM{\boldsymbol }\)
\( \newcommand\BBN{\boldsymbol\RN}\)
\( \newcommand\BBO{\boldsymbol\RO}\)
\( \newcommand\BBP{\boldsymbol\RP}\)
\( \newcommand\BBQ{\boldsymbol\RQ}\)
\( \newcommand\BBR{\boldsymbol\RR}\)
\( \newcommand\BBS{\boldsymbol\RS}\)
\( \newcommand\BBT{\boldsymbol\RT}\)
\( \newcommand\BBU{\boldsymbol\RU}\)
\( \newcommand\BBV{\boldsymbol\RV}\)
\( \newcommand\BBW{\boldsymbol\RW}\)
\( \newcommand\BBX{\boldsymbol\RX}\)
\( \newcommand\BBY{\boldsymbol\RY}\)
\( \newcommand\BBZ{\boldsymbol\RZ}\)
\( \newcommand\BBa{\boldsymbol\Ra}\)
\( \newcommand\BBb{\boldsymbol\Rb}\)
\( \newcommand\BBc{\boldsymbol\Rc}\)
\( \newcommand\BBd{\boldsymbol\Rd}\)
\( \newcommand\BBe{\boldsymbol\Re}\)
\( \newcommand\BBf{\boldsymbol\Rf}\)
\( \newcommand\BBg{\boldsymbol\Rg}\)
\( \newcommand\BBh{\boldsymbol\Rh}\}\)
\( \newcommand\BBi{\boldsymbol\Ri}\)
\( \newcommand\BBj{\boldsymbol\Rj}\)
\( \newcommand\BBk{\boldsymbol\Rk}\)
\( \newcommand\BBl{boldsymbol\Rl}\)
\( \newcommand\BBm{\boldsymbol }\)
\( \newcommand\BBn{\boldsymbol\Rn}\)
\( \newcommand\BBo{\boldsymbol\Ro}\)
\( \newcommand\BBp{\boldsymbol\Rp}\)
\( \newcommand\BBq{\boldsymbol\Rq}\)
\( \newcommand\BBr{\boldsymbol\Rr}\)
\( \newcommand\BBs{\boldsymbol\Rs}\)
\( \newcommand\BBt{\boldsymbol\Rt}\)
\( \newcommand\BBu{\boldsymbol\Ru}\)
\( \newcommand\BBv{\boldsymbol\Rv}\)
\( \newcommand\BBw{\boldsymbol\Rw}\)
\( \newcommand\BBx{\boldsymbol\Rx}\)
\( \newcommand\BBy{\boldsymbol\Ry}\)
\( \newcommand\BBz{\boldsymbol\Rz}\)
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
\( \newcommand\bnabla{\boldsymbol{\nabla}}\)
\( \newcommand\Bell{\boldsymbol\ell}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \newcommand\ns{^\vphantom{*}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}\)
\( \newcommand\izpi{\int\limits_{0}^{\infty}\!\!}\)
\( \newcommand\etc{\it etc.\/}\)
\( \newcommand\etal{\it et al.\/}\)
\( \newcommand\opcit{\it op. cit.\/}\)
\( \newcommand\ie{\it i.e.\/}\)
\( \newcommand\Ie{\it I.e.\/}\)
\( \newcommand\viz{\it viz.\/}\)
\( \newcommand\eg{\it e.g.\/}\)
\( \newcommand\Eg{\it E.g.\/}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \def\sss#1{\scriptscriptstyle #1}\)
\( \def\ss#1{\scriptstyle #1}\)
\( \def\ssr#1{\scriptstyle #1}\)
\( \def\ssf#1{\scriptstyle #1}\)
\( \newcommand\NA{N_{\ssr{\!A}}}\)
\( \newcommand\lala{\langle\!\langle}\)
\( \newcommand\rara{\rangle\!\rangle}\)
\( \newcommand\blan{\big\langle}\)
\( \newcommand\bran{\big\rangle}\)
\( \newcommand\Blan{\Big\langle}\)
\( \newcommand\Bran{\Big\rangle}\)
\( \newcommand\intl{\int\limits}\)
\( \newcommand\half{\frac{1}{2}}\)
\( \newcommand\third{\frac{1}{3}}\)
\( \newcommand\fourth{\frac{1}{4}}\)
\( \newcommand\eighth{\frac{1}{8}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\undertext#1{$\underline{\hbox{#1}}$}\)
\( \newcommand\Tra{\mathop{\textsf{Tr}}\,}\)
\( \newcommand\det{\mathop{\textsf{det}}\,}\)
\( \def\tket#1{|  #1 \rangle}\)
\( \def\tbra#1{\langle #1|}\)
\( \def\tbraket#1#2{\langle #1  |   #2 \rangle}\)
\( \def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}\)
\( \def\sket#1{|  \, #1 \,  \rangle}\)
\( \def\sbra#1{\langle \,  #1 \, |}\)
\( \def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}\)
\( \def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}\)
\(\def\ket#1{\big| \, #1\, \big\rangle}\)
\( \def\bra#1{\big\langle \, #1 \, \big|}\)
\( \def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}\)
\( \def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}\)
\( \newcommand\pz{\partial}\)
\( \newcommand\pzb{\bar{\partial}}\)
\( \newcommand\svph{\vphantom{\int}}\)
\( \newcommand\vph{\vphantom{\sum_i}}\)
\( \newcommand\bvph{\vphantom{\sum_N^N}}\)
\( \newcommand\nd{^{\vphantom{\dagger}}}\)
\( \newcommand\ns{^{\vphantom{*}}}\)
\( \newcommand\yd{^\dagger}\)
\( \newcommand\zb{\bar z}\)
\( \newcommand\zdot{\dot z}\)
\( \newcommand\zbdot{\dot{\bar z}}\)
\( \newcommand\kB{k_{\sss{B}}}\)
\( \newcommand\kT{k_{\sss{B}}T}\)
\( \newcommand\gtau{g_\tau}\)
\( \newcommand\Htil{\tilde H}\)
\( \newcommand\pairo{(\phi\nd_0,J\nd_0)}\)
\( \newcommand\pairm{(\phi\nd_0,J)}\)
\( \newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}\)
\( \newcommand\pairmb{(\Bphi\nd_0,\BJ)}\)
\( \newcommand\pair{(\phi,J)}\)
\( \newcommand\Hz{H\nd_0}\)
\( \newcommand\Ho{H\nd_1}\)
\( \newcommand\Htz{\Htil\nd_0}\)
\( \newcommand\Hto{\Htil\nd_1}\)
\( \newcommand\oc{\omega_\Rc}\)

\(\newcommand \gtwid{\approx}\)

\( \newcommand\index{\textsf{ind}}\)
\( \newcommand\csch{\,{ csch\,}}\)
\( \newcommand\ctnh{\,{ ctnh\,}}\)
\( \newcommand\ctn{\,{ ctn\,}}\)
\( \newcommand\sgn{\,{ sgn\,}}\)
\( \def\tmapright#1{\xrightarrow \limits^{#1}}\)
\( \def\bmapright#1{\xrightarrow\limits_{#1}}\)
\( \newcommand\hfb{\hfill\break}\)
\( \newcommand\Rep{\textsf{Re}\,}\)
\( \newcommand\Imp{\textsf{Im}\,}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }\)
\( \def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }\)
\( \newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}\)

\( \def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}\)
\( \def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}\)
\( \def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}\)
\( \def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}\)
\( \newcommand\subA{\ns_\ssr{A}}\)
\( \newcommand\subB{\ns_\ssr{B}}\)
\( \newcommand\subC{\ns_\ssr{C}}\)
\( \newcommand\subD{\ns_\ssr{D}}\)
\( \newcommand\subAB{\ns_\ssr{AB}}\)
\( \newcommand\subBC{\ns_\ssr{BC}}\)
\( \newcommand\subCD{\ns_\ssr{CD}}\)
\( \newcommand\subDA{\ns_\ssr{DA}}\)
\( \def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }\)
\( \def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}\)
\( \newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}\)
\( \newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}\)
\( \newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}\)
\( \newcommand\cds{\,\bullet\,}\)
\( \newcommand\ccs{\,\circ\,}\)
\( \newcommand\nsub{_{\vphantom{\dagger}}}\)
\( \newcommand\rhohat{\hat\rho}\)
\( \newcommand\vrhhat{\hat\vrh}\)
\( \newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}\)
\( \newcommand\brangle{\big\rangle}\)
\( \newcommand\blangle{\big\langle}\)
\( \newcommand\vet{\tilde\ve}\)
\( \newcommand\zbar{\bar z}\)
\( \newcommand\ftil{\tilde f}\)
\( \newcommand\XBE{\RXi\ns_\ssr{BE}}\)
\( \newcommand\XFD{\RXi\ns_\ssr{FD}}\)
\( \newcommand\OBE{\Omega\ns_\ssr{BE}}\)
\( \newcommand\OFD{\Omega\ns_\ssr{FD}}\)
\( \newcommand\veF{\ve\ns_\RF}\)
\( \newcommand\kF{k\ns_\RF}\)
\( \newcommand\kFu{k\ns_{\RF\uar}}\)
\( \newcommand\SZ{\textsf Z}}\) \( \newcommand\kFd{k\ns_{\RF\dar}\)
\( \newcommand\muB{\mu\ns_\ssr{B}}\)
\( \newcommand\mutB{\tilde\mu}\ns_\ssr{B}\)
\( \newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}\)
\( \newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}\)
\( \newcommand\xhiOZ{\xhi^\ssr{OZ}}\)
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\jhz{\HJ(0)}\)
\( \newcommand\nda{\nd_\alpha}\)
\( \newcommand\ndap{\nd_{\alpha'}}\)
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.08:_Selected_Examples), /content/body/p/span, line 1, column 23

\)
\( \newcommand\msa{m\ns_\ssr{A}}\)
\( \newcommand\msb{m\ns_\ssr{B}}\)
\( \newcommand\mss{m\ns_\Rs}\)
\( \newcommand\HBx{\hat\Bx}\)
\( \newcommand\HBy{\hat\By}\)
\( \newcommand\HBz{\hat\Bz}\)
\( \newcommand\thm{\theta\ns_m}\)
\( \newcommand\thp{\theta\ns_\phi}\)
\( \newcommand\mtil{\widetilde m}\)
\( \newcommand\phitil{\widetilde\phi}\)
\( \newcommand\delf{\delta\! f}\)
\( \newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}\)
\( \newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}\)
\( \newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}\)
\( \newcommand\vbar{\bar v}\)
\( \newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}\)
\( \newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}\)
\( \newcommand\gla{g\nd_{\RLambda\nd}}\)
\( \newcommand\TA{T\ns_\ssr{A}}\)
\( \newcommand\TB{T\ns_\ssr{B}}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \newcommand\NS{N\ns_{\textsf S}}\)

Spins in an External Magnetic Field

Consider a system of \(\NS\) spins, each of which can be either up \((\sigma=+1)\) or down (\(\sigma=-1\)). The Hamiltonian for this system is

\[\HH=-\mu\ns_0 H\sum_{j=1}^{\NS} \sigma\ns_j\ ,\]

where now we write \(\HH\) for the Hamiltonian, to distinguish it from the external magnetic field \(H\), and \(\mu\ns_0\) is the magnetic moment per particle. We treat this system within the ordinary canonical ensemble. The partition function is

\[Z=\sum_{\sigma\ns_1}\cdots\sum_{\sigma\ns_{\NS}} e^{-\beta \HH} = \zeta^{\NS}\ ,\]

where \(\zeta\) is the single particle partition function:

\[\zeta=\sum_{\sigma=\pm 1} e^{\mu\ns_0 H\sigma/\kT}=2\cosh\!\bigg({\mu\ns_0 H\over \kT}\bigg)\ .\]

The Helmholtz free energy is then

\[F(T,H,\NS)=-\kT\ln Z=-\NS\,\kT\ln\!\Bigg[ 2\cosh\!\bigg({\mu\ns_0 H\over \kT}\bigg)\Bigg]\ . \label{freespin}\]

The magnetization is

\[M=-\pabc{F}{H}{T,\,\NS}=\NS\,\mu\ns_0\tanh\!\bigg({\mu\ns_0 H\over \kT}\bigg)\ . \label{fsmag}\]

The energy is

\[E={\pz\over\pz\beta}\,\big(\beta F\big)=-\NS\,\mu\ns_0 H\tanh\!\bigg({\mu\ns_0 H\over \kT}\bigg)\ . \label{sperg}\]

Hence, \(E=-H M\), which we already knew, from the form of \(\HH\) itself.

Each spin here is independent. The probability that a given spin has polarization \(\sigma\) is

\[P\ns_\sigma={e^{\beta\mu\ns_0 H\sigma}\over e^{\beta\mu\ns_0 H} + e^{-\beta\mu\ns_0 H} }\ .\]

The total probability is unity, and the average polarization is a weighted average of \(\sigma=+1\) and \(\sigma=-1\) contributions:

\[P\ns_\uar+ P\ns_\dar=1 \qquad,\qquad \langle\sigma\rangle = P\ns_\uar - P\ns_\dar =\tanh\!\bigg({\mu\ns_0 H\over \kT}\bigg)\ .\]

At low temperatures \(T\ll\mu\ns_0 H/\kB\), we have \(P\ns_\uar \approx 1-e^{-2\mu\ns_0 H/\kT}\). At high temperatures \(T\>> \mu\ns_0 H/\kB\), the two polarizations are equally likely, and \(P\ns_\sigma\approx \half \Big(1+\frac{\sigma\mu\ns_0 H}{\kT}\Big)\).

The isothermal magnetic susceptibility is defined as

\[\xhi\ns_T={1\over\NS}\pabc{M}{H}{T}={\mu_0^2\over\kT}\>{sech}^2\!\bigg({\mu\ns_0 H\over \kT}\bigg)\ . \label{magsus}\]

(Typically this is computed per unit volume rather than per particle.) At \(H=0\), we have \(\xhi\ns_T=\mu_0^2/\kT\), which is known as the Curie law.

Aside

The energy \(E=-H M\) here is not the same quantity we discussed in our study of thermodynamics. In fact, the thermodynamic energy for this problem vanishes! Here is why. To avoid confusion, we’ll need to invoke a new symbol for the thermodynamic energy, \(\CE\). Recall that the thermodynamic energy \(\CE\) is a function of extensive quantities, meaning \(\CE=\CE(S,M,\NS)\). It is obtained from the free energy \(F(T,H,\NS)\) by a double Legendre transform:

\[\CE(S,M,\NS)=F(T,H,\NS)+ TS + H M\ .\]

Now from Equation \ref{freespin} we derive the entropy

\[S=-{\pz F\over\pz T}=\NS\,\kB\ln\!\Bigg[ 2\cosh\!\bigg({\mu\ns_0 H\over \kT}\bigg)\Bigg]-\NS\,{\mu\ns_0 H\over T}\, \tanh\!\bigg({\mu\ns_0 H\over \kT}\bigg)\ .\]

Thus, using Equations \ref{freespin} and \ref{fsmag}, we obtain \(\CE(S,M,\NS)=0\).

The potential confusion here arises from our use of the expression \(F(T,H,\NS)\). In thermodynamics, it is the Gibbs free energy \(G(T,p,N)\) which is a double Legendre transform of the energy: \(G=\CE-TS+pV\). By analogy, with magnetic systems we should perhaps write \(G=\CE-TS-H M\), but in keeping with many textbooks we shall use the symbol \(F\) and refer to it as the Helmholtz free energy. The quantity we’ve called \(E\) in Equation \ref{sperg} is in fact \(E=\CE-H M\), which means \(\CE=0\). The energy \(\CE(S,M,\NS)\) vanishes here because the spins are noninteracting.

Negative Temperature (!)

Consider again a system of \(\NS\) spins, each of which can be either up \((+)\) or down (\(-\)). Let \(N\ns_\sigma\) be the number of sites with spin \(\sigma\), where \(\sigma=\pm 1\). Clearly \(N\ns_+ + N\ns_- = \NS\). We now treat this system within the microcanonical ensemble.

Figure \(\PageIndex{1}\): When entropy decreases with increasing energy, the temperature is negative. Typically, kinetic degrees of freedom prevent this peculiarity from manifesting in physical systems.

The energy of the system is

\[E=-H M\ ,\]

where \(H\) is an external magnetic field, and \(M=(N\ns_+ - N\ns_-)\,\mu\ns_0\) is the total magnetization. We now compute \(S(E)\) using the ordinary canonical ensemble. The number of ways of arranging the system with \(N\ns_+\) up spins is

\[\ROmega={\NS\choose N\ns_+}\ ,\]

hence the entropy is

\[S=\kB\ln\ROmega=-\NS\,\kB\Big\{x\ln x + (1-x)\ln (1-x)\Big\}\]

in the thermodynamic limit: \(\NS\to\infty\), \(N\ns_+\to\infty\), \(x=N\ns_+/\NS\) constant. Now the magnetization is \(M=(N\ns_+ - N\ns_-)\mu\ns_0 = (2N\ns_+ - \NS)\mu\ns_0\), hence if we define the maximum energy \(E\ns_0\equiv \NS\,\mu\ns_0 H\), then

\[{E\over E\ns_0}=-{M\over\NS\,\mu\ns_0} = 1-2x \qquad\Longrightarrow\qquad x={E\ns_0 - E\over 2 E\ns_0}\ .\]

We therefore have

\[S(E,\NS)=-\NS\,\kB\Bigg[ \bigg({E\ns_0 - E\over 2 E\ns_0}\bigg)\ln\!\bigg({E\ns_0 - E\over 2 E\ns_0}\bigg) + \bigg({E\ns_0 + E\over 2 E\ns_0}\bigg)\ln\!\bigg({E\ns_0 + E\over 2 E\ns_0}\bigg)\Bigg]\ .\]

We now have

\[{1\over T}=\pabc{S}{E}{\NS}={\pz S\over \pz x}\,{\pz x\over\pz E}= {\NS\,\kB\over 2E\ns_0}\,\ln\!\bigg({E\ns_0-E\over E\ns_0+E}\bigg)\ .\]

We see that the temperature is positive for \(-E\ns_0\le E < 0\) and is negative for \(0<E\le E\ns_0\).

What has gone wrong? The answer is that nothing has gone wrong – all our calculations are perfectly correct. This system does exhibit the possibility of negative temperature. It is, however, unphysical in that we have neglected kinetic degrees of freedom, which result in an entropy function \(S(E,\NS)\) which is an increasing function of energy. In this system, \(S(E,\NS)\) achieves a maximum of \(S\ns_{max}=\NS\,\kB\ln 2\) at \(E=0\) ( \(x=\half\)), and then turns over and starts decreasing. In fact, our results are completely consistent with Equation \ref{sperg}: the energy \(E\) is an odd function of temperature. Positive energy requires negative temperature! Another example of this peculiarity is provided in the appendix in §11.2.

Adsorption

PROBLEM: A surface containing \(\NS\) adsorption sites is in equilibrium with a monatomic ideal gas. Atoms adsorbed on the surface have an energy \(-\RDelta\) and no kinetic energy. Each adsorption site can accommodate at most one atom. Calculate the fraction \(f\) of occupied adsorption sites as a function of the gas density \(n\), the temperature \(T\), the binding energy \(\RDelta\), and physical constants.

The grand partition function for the surface is

\[\begin{split} \Xi\nd_{surf}=e^{-\ROmega\nd_{surf}/\kT}&=\sum_{j=0}^{\NS} {\NS\choose j}\,e^{j(\mu+\RDelta)/\kT}\\ &=\big(1+e^{\mu/\kT}\,e^{\RDelta/\kT}\big)^{\NS}\ . \end{split}\]

The fraction of occupied sites is

\[f={\langle \HN\nd_{surf}\rangle\over \NS}=-{1\over \NS}\,{\pz\ROmega\nd_{surf}\over\pz\mu}= {e^{\mu/\kT}\over e^{\mu/\kT} + e^{-\RDelta/\kT}}\ .\]

Since the surface is in equilibrium with the gas, its fugacity \(z=\exp(\mu/\kT)\) and temperature \(T\) are the same as in the gas.

SOLUTION: For a monatomic ideal gas, the single particle partition function is \(\zeta=V\lambda_T^{-3}\), where \(\lambda\nd_T=\sqrt{2\pi\hbar^2/m\kT}\) is the thermal wavelength. Thus, the grand partition function, for indistinguishable particles, is

\[\Xi\nd_{gas}=\exp\Big(V\lambda_T^{-3}\,e^{\mu/\kT}\Big)\ .\]

The gas density is

\[n={\langle \HN\nd_{gas}\rangle\over V}=-{1\over V}\>{\pz\ROmega\nd_{gas}\over\pz\mu}=\lambda_T^{-3}\,e^{\mu/\kT}\ .\]

We can now solve for the fugacity: \(z=e^{\mu/\kT}=n\lambda_T^3\). Thus, the fraction of occupied adsorption sites is

\[f={n\lambda_T^3\over n\lambda_T^3 + e^{-\RDelta/\kT}}\ .\]

Interestingly, the solution for \(f\) involves the constant \(\hbar\).

It is always advisable to check that the solution makes sense in various limits. First of all, if the gas density tends to zero at fixed \(T\) and \(\RDelta\), we have \(f\to 0\). On the other hand, if \(n\to\infty\) we have \(f\to 1\), which also makes sense. At fixed \(n\) and \(T\), if the adsorption energy is \((-\RDelta)\to-\infty\), then once again \(f=1\) since every adsorption site wants to be occupied. Conversely, taking \((-\RDelta)\to +\infty\) results in \(n\to 0\), since the energetic cost of adsorption is infinitely high.

Figure \(\PageIndex{2}\): The monomers in wool are modeled as existing in one of two states. The low energy undeformed state is A, and the higher energy deformed state is B. Applying tension induces more monomers to enter the B state.

Elasticity of wool

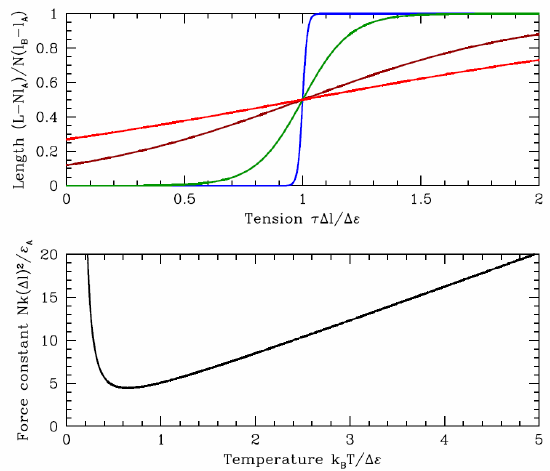
Wool consists of interlocking protein molecules which can stretch into an elongated configuration, but reversibly so. This feature gives wool its very useful elasticity. Let us model a chain of these proteins by assuming they can exist in one of two states, which we will call A and B, with energies \(\ve\subA\) and \(\ve\subB\) and lengths \(\ell\subA\) and \(\ell\subB\). The situation is depicted in Figure \(\PageIndex{2}\). We model these conformational degrees of freedom by a spin variable \(\sigma=\pm 1\) for each molecule, where \(\sigma=+1\) in the A state and \(\sigma=-1\) in the B state. Suppose a chain consisting of \(N\) monomers is placed under a tension \(\tau\). We then have

\[\HH=\sum_{j=1}^N \Big[\ve\subA\,\delta\ns_{\sigma\ns_j,+1} + \ve\subB\,\delta\ns_{\sigma\ns_j,-1}\Big]\ .\]

Similarly, the length is

\[\HL=\sum_{j=1}^N \Big[\ell\subA\,\delta\ns_{\sigma\ns_j,+1} + \ell\subB\,\delta\ns_{\sigma\ns_j,-1}\Big]\ .\]

The Gibbs partition function is \(Y=\Tra e^{-\HK/\kT}\), with \(\HK=\HH-\tau \HL\) :

\[\HK=\sum_{j=1}^N \Big[\vet\subA\,\delta\ns_{\sigma\ns_j,+1} + \vet\subB\,\delta\ns_{\sigma\ns_j,-1}\Big]\ ,\]

where \(\vet\subA\equiv\ve\subA-\tau\ell\subA\) and \(\vet\subB\equiv\ve\subB-\tau\ell\subB\). At \(\tau=0\) the A state is preferred for each monomer, but when \(\tau\) exceeds \(\tau^*\), defined by the relation \(\vet\subA=\vet\subB\), the B state is preferred. One finds

\[\tau^*={\ve\subB-\ve\subA\over\ell\subB-\ell\subA}\ .\]

Figure \(\PageIndex{3}\): Upper panel: length \(L(\tau,T)\) for \(k_{\ssr{B}}T/\vet=0.01\) (blue), \(0.1\) (green), \(0.5\) (dark red), and \(1.0\) (red). Bottom panel: dimensionless force constant \(k/N(\RDelta\ell)^2\) versus temperature.

Once again, we have a set of \(N\) noninteracting spins. The partition function is \(Y=\zeta^N\), where \(\zeta\) is the single monomer partition function, \(\zeta=\Tra e^{-\beta \Hh}\), where

\[\Hh=\vet\subA\,\delta\ns_{\sigma\ns_j,1} + \vet\subB\,\delta\ns_{\sigma\ns_j,-1}\]

is the single “spin" Hamiltonian. Thus,

\[\zeta=\Tra e^{-\beta \Hh} = e^{-\beta\vet\ns_\RA} + e^{-\beta\vet\ns_\RB}\ ,\]

It is convenient to define the differences

\[\RDelta\ve=\ve\subB-\ve\subA\quad,\quad \RDelta\ell=\ell\subB-\ell\subA\quad,\quad \RDelta\vet=\vet\subB-\vet\subA\]

in which case the partition function \(Y\) is

\[\begin{aligned} Y(T,\tau,N)&=e^{-N\beta\,\vet\ns_\RA}\Big[1+e^{-\beta\RDelta\vet}\Big]^N\\ G(T,\tau,N)&=N\vet\subA - N\kT\ln\!\Big[1+e^{-\RDelta\vet/\kT}\Big]\end{aligned}\]

The average length is

\[\begin{split} L=\langle \HL\rangle &= -\pabc{G}{\tau}{T,N}\\ &=N\ell\subA + {N\RDelta\ell\over e^{(\RDelta\ve-\tau\RDelta\ell)/\kT}+1}\ . \end{split}\]

The polymer behaves as a spring, and for small \(\tau\) the spring constant is

\[k={\pz \tau\over\pz L}\bigg|\nd_{\tau=0}={4\kT\over N(\RDelta\ell)^2}\,\cosh^2\!\bigg({\RDelta\ve\over 2\kT}\bigg)\ .\]

The results are shown in Figure \(\PageIndex{3}\). Note that length increases with temperature for \(\tau < \tau^*\) and decreases with temperature for \(\tau>\tau^*\). Note also that \(k\) diverges at both low and high temperatures. At low \(T\), the energy gap \(\RDelta \ve\) dominates and \(L=N\ell\ns_\ssr{A}\), while at high temperatures \(\kT\) dominates and \(L=\half N(\ell\ns_\ssr{A}+\ell\ns_\ssr{B})\).

Noninteracting spin dimers

Consider a system of noninteracting spin dimers as depicted in Figure \(\PageIndex{4}\). Each dimer contains two spins, and is described by the Hamiltonian

\[\HH\ns_{dimer}=-J\,\sigma\ns_1\sigma\ns_2 - \mu\ns_0 H\,(\sigma\ns_1 +\sigma\ns_2)\ .\]

Here, \(J\) is an interaction energy between the spins which comprise the dimer. If \(J>0\) the interaction is ferromagnetic, which prefers that the spins are aligned. That is, the lowest energy states are \(\sket{\!\!\uar\uar}\) and \(\sket{\!\!\dar\dar}\). If \(J<0\) the interaction is antiferromagnetic, which prefers that spins be anti-aligned: \(\sket{\!\!\uar\dar}\) and \(\sket{\!\!\dar\uar}\).⁹

Suppose there are \(N\ns_\Rd\) dimers. Then the OCE partition function is \(Z=\zeta^{N\ns_\Rd}\), where \(\zeta(T,H)\) is the single dimer partition function. To obtain \(\zeta(T,H)\), we sum over the four possible states of the two spins, obtaining

\[\begin{split} \zeta&={Tr}\,e^{- \HH\ns_{dimer}/\kT}\nonumber\\ &=2\,e^{-J/\kT} + 2\,e^{J/\kT}\cosh\!\bigg({2\mu\ns_0 H\over\kT}\bigg)\ . \end{split}\]

Thus, the free energy is

\[F(T,H,N\ns_\Rd)=-N\ns_\Rd\,\kT\ln 2 - N\ns_\Rd\,\kT\ln\!\Bigg[ e^{-J/\kT} + e^{J/\kT}\cosh\!\bigg({2\mu\ns_0 H\over\kT}\bigg)\Bigg]\ .\]

The magnetization is

\[M=-\pabc{F}{H}{T,N\ns_\Rd}=2N\ns_\Rd\,\mu\ns_0\cdot {e^{J/\kT}\sinh\!\Big({2\mu\ns_0 H\over\kT}\Big)\over e^{-J/\kT} + e^{J/\kT}\cosh\!\Big({2\mu\ns_0 H\over\kT}\Big)}\]

It is instructive to consider the zero field isothermal susceptibility per spin,

\[\xhi\nd_T={1\over 2N\ns_\Rd}\,{\pz M\over\pz H}\bigg|\nd_{H=0} ={\mu_0^2\over\kT}\cdot{2\,e^{J/\kT}\over e^{J/\kT} + e^{-J/\kT}}\ .\]

The quantity \(\mu_0^2/\kT\) is simply the Curie susceptibility for noninteracting classical spins. Note that we correctly recover the Curie result when \(J=0\), since then the individual spins comprising each dimer are in fact noninteracting. For the ferromagnetic case, if \(J\gg\kT\), then we obtain

\[\xhi\ns_T(J\gg\kT)\approx{2\mu_0^2\over\kT}\ .\]

This has the following simple interpretation. When \(J\gg\kT\), the spins of each dimer are effectively locked in parallel. Thus, each dimer has an effective magnetic moment \(\mu\ns_{eff}=2\mu\ns_0\). On the other hand, there are only half as many dimers as there are spins, so the resulting Curie susceptibility per spin is \(\half\times (2\mu_0)^2/\kT\).

Figure \(\PageIndex{4}\): A model of noninteracting spin dimers on a lattice. Each red dot represents a classical spin for which \(\sigma_j=\pm 1\).

When \(-J\gg\kT\), the spins of each dimer are effectively locked in one of the two antiparallel configurations. We then have

\[\xhi\ns_T(-J\gg\kT)\approx {2\mu_0^2\over\kT}\,e^{-2|J|/\kT}\ .\]

In this case, the individual dimers have essentially zero magnetic moment.