21.1: Magnetic fields
( \newcommand{\kernel}{\mathrm{null}\,}\)
Just as we can model the electric force on a charge by using the electric field (e.g. from another charge), we can model the force on a magnet by using a magnetic field (e.g. from another magnet). In your experience, every magnet that you have seen always has a “North” pole and a “South” pole. Most likely, you have noticed that the North pole of a magnet is attracted to the South pole of another magnet, and that the two North (or South) poles of different magnets repel each other. Thus, the magnetic force is attractive between two opposite poles, and repulsive otherwise.
The Earth itself can be modeled as a giant bar magnet, with North and South magnetic poles. The poles on a magnet are labeled North and South according to which geographic pole of the Earth they are attracted to (a magnetic compass needle has a magnetic North pole on the side that point to the Earth’s North geographic pole).
Is the magnetic North pole of the Earth located closer to the Earth’s geographic North pole or closer to its geographic South Pole?
- Earth does not have a magnetic field.
- Earth’s magnetic North pole is at Earth’s geographic North pole.
- Earth’s magnetic North pole is at Earth’s geographic South pole.
- Earth’s magnetic North pole depends on the charge of the observer.
- Answer
-
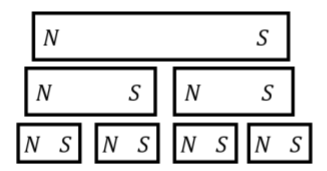
It may seem that the magnetic force can be described in the same way as the electric force, having two opposite sign “charges” (or poles for magnets), although this is not the case. As far as we can tell, there are no magnets that have only a North or a South pole. Every magnet must have a North and a South pole. This is fundamentally different from the electric force, where an object can have a net positive or negative charge. In the context of magnetism, we say that “monopoles do not exist” (an object that has only a North or a South pole would be called a monopole). This is illustrated in Figure 21.1.1, which shows what happens as one cuts a bar magnet into two pieces; rather than ending up with a North and a South piece (monopoles), we end up with two smaller bar magnets, each with their own North and South poles, and so on if we try to subdivide the magnets further.
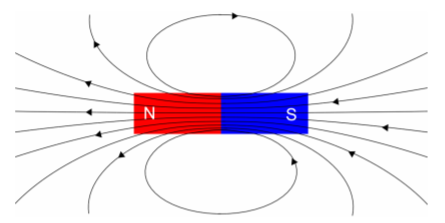
We model the magnetic force using a magnetic field vector, usually labeled, →B. The magnitude of the magnetic field has the S.I. units of Teslas (T). We draw magnetic field lines in much the same way that we draw electric field lines. The magnetic field lines are such that the magnetic field vector, →B, at some point in space is tangent to the field line at that point. The strength of the magnetic field is determined by the density of field lines at that position in space. The direction of the magnetic field, →B, indicates the direction of the force that is exerted on the North pole of a magnet. Magnetic field lines thus flow away from North poles and towards South poles.
The magnetic field description is similar to that of the electric field, with North magnetic poles being similar to positive electric charges, and vice versa. However, because magnetic monopoles do not exist, magnetic field lines do not end (or start) on the pole of a magnet. Rather, magnetic field lines must always form closed loops. Figure 21.1.2 shows the magnetic field lines for a bar magnet, highlighting that the field lines do not end at the poles, but rather continue through the magnet (and some of the lines only “close” outside of the figure). The magnetic field from a bar magnet is very similar to the electric field created by an electric dipole (and for that reason, we often use the term magnetic dipole to describe objects that create a magnetic field with the same shape).
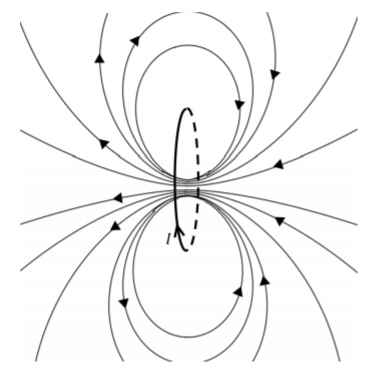
We will discuss how to model magnetic fields in the next chapter, but it is important to understand that magnetic fields are created by moving electric charges. The electrons in the material that forms a bar magnet are the moving charges that create the magnetic field. As we will see, the magnetic field from a charge moving around in a circle (or a circular loop of current), has exactly the same shape as that of a bar magnet, as illustrated in Figure 21.1.3. We can thus think of charge moving in a circle as a small bar magnet, or more precisely, as a magnetic dipole.
In a magnet, the electrons in the material are moving in such a way that the magnetic fields that they generate are all in the same direction. Each atom is like a small magnetic dipole, and all of these are aligned. This allows us to understand why cutting a magnet does not result in two monopoles (Figure 21.1.1): when we cut the bar magnet, we end up with less material, but each piece of material still contains magnetic dipoles that are aligned with each other, each having a North and South side. Note that it is not the motion of electrons around their nuclei that results in the magnetic field, and that one requires quantum mechanics and the notion of “spin” to describe this all in detail.
Most materials will respond to magnetic fields, but the behavior is most evident in “ferromagnetic” materials, such as iron (Fe). Ferromagnetic materials can be magnetized by an external magnetic field, effectively transforming them into magnets. One can think of a material as containing many little magnetic dipoles (from the motion of the electrons), which themselves are like bar magnets. If that material is ferromagnetic, an external magnetic field can act on the little “bar magnets”, orienting them all in the same way, so that the material as a whole becomes magnetic. For some ferromagnetic materials, that common orientation will remain when the external magnetic field is removed, creating a “permanent magnet”. For other ferromagnetic materials, the common orientation disappears when the external field is removed; those materials are thus attracted to a magnet, but they cannot form a magnet.

