21.2: The magnetic force on a moving charge

review topics

Section A1.3 on the vector product.

When an electric charge, \(q\), has a velocity, \(\vec v\), relative to a magnetic field, \(\vec B\), a magnetic force is exerted on the particle:

\[\vec F_{B}=q\vec v\times\vec B\]

We can make a few remarks about the magnetic force:

• The magnetic force is always perpendicular to the velocity and to the magnetic field (since it is given by their cross-product).
• The direction of the magnetic force depends on the sign of the charge.
• The magnetic force can do no work, since it is always perpendicular to the velocity (and thus to displacement).
• There is no force if the particle’s velocity is in the same direction as the magnetic field vector.
• The force increases with charge, speed, and strength of the magnetic field.

Exercise \(\PageIndex{1}\)

A proton moves East in Earth’s magnetic field, which way is it deflected?

1. Away from the Earth.
2. Towards the Earth.
3. North.
4. South.

Answer

Exercise \(\PageIndex{2}\)

An electron moves West in Earth’s magnetic field, which way is it deflected?

1. Away from the Earth.
2. Towards the Earth.
3. North.
4. South.

Answer

josh's thoughts

It is very important to remember what each part of the right-hand rule for cross-products represents. To help remember what each finger represents, I say "velocity" as I extend my thumb, "field" as I extend my index finger, and "force" as I extend my middle finger. When using the right hand rule, it is also important to remember the \(q\) in the equation \(\vec F_B = q\vec v \times \vec B\). This \(q\) could be negative, which would mean that the force acts in the opposite direction.

Figure \(\PageIndex{1}\): The way that Josh remembers the right hand rule for magnetism.

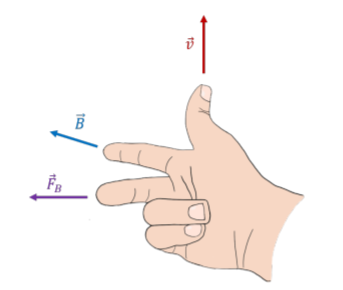
If you find yourself forgetting the right-hand rule on a test or exam, just remember that you can still find the correct answer by setting up a three-dimensional coordinate system and evaluating the cross product.

You should be somewhat bothered by the fact that the force depends on the velocity of the charge, since velocity depends on the frame of reference from which it is measured. The above equation has a strange implication: if we observe an electron moving in a magnetic field, we will see its motion be deflected by the magnetic field. If we move along with the electron, so that it has a velocity of zero in our frame of reference, we should not see the electron being deflected, since the magnetic force would be zero. Clearly, the motion of the electron cannot depend on the frame of reference from which we observe it. Thus, the only way that this equation can make sense is if the magnetic field also depends on our frame of reference. We will revisit this in a subsequent chapter, but for now, remember that this equation only makes sense if the velocity is measured in the same reference frame as that in which the magnetic field is defined.

Another bothersome issue with the magnetic force is that it appears to depend on the fact that most humans are right-handed. Indeed, the direction of the force requires one to use the right-hand rule, which appears arbitrary. This is a common occurrence in physics, as many quantities are defined using a cross-product. However, no physical quantity can ever depend on our choice of right or left hand for determining cross-products. It turns out that any physical quantity (such as the force on a particle, which will deflect the particle in a clearly identifiable direction that does not depends on human’s choice of right and left), always depends on two successive applications of the right-hand rule. In this case, the direction of the magnetic field is also given by a right-hand rule applied to the moving charges that create the field (as we will see in the next chapter). The successive uses of the right hand twice “cancel”; one finds that a charge is deflected in the same direction if one had used the left hand to define the magnetic field, and then again the left-hand for the cross-product! We will revisit this issue in the next chapter.

Consider the motion of a charged particle in a region where the magnetic field is uniform (constant in magnitude and direction). If the velocity vector of the particle is perpendicular to the magnetic field, the particle will undergo uniform circular motion, as illustrated in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): The motion of a charged particle in a uniform magnetic field (out of the page) is uniform circular motion.

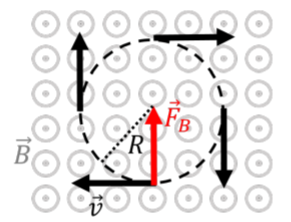
Indeed, the force is always perpendicular to the velocity, and the force is constant in magnitude since both the speed and magnetic field remain constant. These are the only conditions required for uniform circular motion. We can easily determine the radius, \(R\), of the circle, since the magnetic force is responsible for the centripetal acceleration:

\[\begin{aligned} F_B &= m\frac{v^2}{R}\\[4pt] qvB &= m\frac{v^2}{R}\\[4pt] \therefore R &= \frac{mv}{qB}\end{aligned}\]

The radius is called the “cyclotron radius”.

Exercise \(\PageIndex{3}\)

Is the particle illustrated in Figure \(\PageIndex{2}\) positively or negatively charged?

1. The particle is positively charged.
2. The particle is negatively charged.
3. Not enough information to tell.
4. The particle has no charge.

Answer

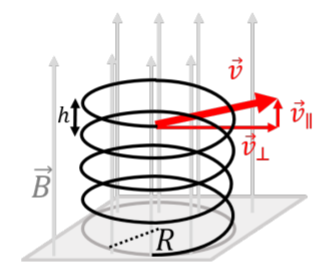
Referring to Figure \(\PageIndex{2}\), if the velocity of the particle is in the plane of the page (perpendicular to the magnetic field), as illustrated, the particle will undergo uniform circular motion. If the velocity of the particle has a component that is parallel to the magnetic field (for example a component coming out of the page, towards you), the particle will undergo “helical motion” (a spiral). The radius of the helix is determined by the component of the velocity, \(\vec v_{\perp}\), that is perpendicular the magnetic field:

\[\begin{aligned} \therefore R &= \frac{mv_{\perp}}{qB}\end{aligned}\]

The charged particle would also have a component of velocity towards you that is constant, resulting in the spiral motion illustrated in Figure \(\PageIndex{3}\). Note that the distance between two spirals (labeled \(h\) in the figure) is called the “pitch”, and is determined by the component of velocity that is parallel to the magnetic field, \(\vec v_\parallel\), since that component is not affected by the magnetic force.

Figure \(\PageIndex{3}\): The helical motion of a charged particle with a component of velocity parallel to the magnetic field. The distance, \(h\), between spirals is called the “pitch”.

Example \(\PageIndex{1}\)

A particle of unknown charge and unknown mass is observed to undergo uniform circular motion with a period, \(T\), when traveling perpendicular to a uniform magnetic field, \(B\). What is the ratio of the particle’s charge to its mass, \(q/m\)?

Solution

We can use the period of the motion to determine the speed of the particle in terms of the radius of the circular path:

\[\begin{aligned} v = \frac{2\pi R}{T}\end{aligned}\]

and then use the equation for the cyclotron radius to relate this to the charge-to-mass ratio of the particle:

\[\begin{aligned} R &= \frac{mv}{qB}\\[4pt] &= \frac{2\pi R m}{qBT}\\[4pt] \therefore \frac{q}{m} &= \frac{2\pi}{BT} \end{aligned}\]

Discussion

When a charged particle undergoes uniform circular motion in a magnetic field, the radius of the motion depends on the particle’s charge-to-mass ratio. This can often be used to measure the mass of, say, an ion, if the charge of the ion is known (usually one or two units of the electron charge). A mass spectrometer makes use of this principle in order to determine the composition of a sample. The sample is vaporized and ionized, the ions are then accelerated using an electric potential difference, before they undergo uniform circular motion. Ions of different masses (and same charge) will then undergo circular motion with different radii, which allows their masses to be determined, and thus the composition of the sample to be known.