24.6: Lorentz transformations and space-time
- Page ID
- 19556
Four-dimensional space-time
So far, we have seen that our notions of time intervals (the time between two events) and space intervals (the distance between two locations) depend on our frame of reference. We also saw how space and time are connected, for example by the fact that time-dilation must go hand-in-hand with length contraction. We also concluded that there is no absolute concept of time, and that time is relative (depends on your frame of reference).
In the context of Special Relativity, we introduce the concept of space-time. To describe the location of an object in space-time, we must specify both the location/position coordinates (\(x\), \(y\), \(z\)) and the time “coordinate”, \(t\). Since time, \(t\), has the dimension of time, we usually specify the time coordinate by multiplying it by speed of light, \(ct\), so that it has dimensions of length. Thus, position in space-time is given by 4 coordinates: \((x,y,z,ct)\).
Space-time diagrams
It is practically impossible to visualize situations in three dimensions, so four dimensions is hopeless! However, we can gain a lot of insight into Special Relativity models by using “space-time diagrams”. In a space-time diagram, we use only one of the space coordinates (typically \(x\)) along with the time coordinate, \(ct\), to define the two axes of a space-time diagram. Space-time diagrams are analogous to “position as a function of time” graphs that one would draw in kinematics, although they are fundamentally different in that, for a space-time diagram, the coordinates should be thought of as independent (one is not plotting a dependent variable as a function of an independent variable).
Figure \(\PageIndex{1}\) shows a space-time diagram for an object that was located at position \(x=x_1\) at time \(t=t_1\) (location \(A\)), and at position \(x=x_2\) at time \(t=t_2\) (location \(B\)). The path of an object through space-time, indicated by the line that connects \(A\) and \(B\), is called the “world line” of the object.
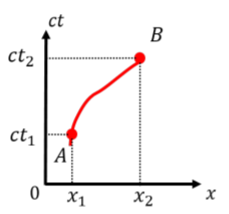
What does the world-line of a stationary particle look like?
- A vertical line.
- A horizontal line.
- A point.
- Answer
-
A pulse of light traveling in the \(x\) direction will always have a world-line that makes a \(45^{\circ}\) angle with the horizontal (space) axis (since \(x=ct\)). The world line of any object that travels with a speed below the speed of light must always make an angle with the horizontal axis that is greater than \(45^{\circ}\).
A position in space-time is usually called an “event”. We can draw a set of lines, at \(45^{\circ}\) degrees from the horizontal axis, that intersect at an event in space-time. Those lines define two “light cones” corresponding to: (1) locations in space-time in the past that could have had a causal effect on the event (the “past light cone”), and (2), locations in space-time in the future for which the event can have a causal effect (the “future light cone”).
Figure \(\PageIndex{2}\) shows the light cones associated with an event, \(A\), in space-time. The past light cone is the only region of space-time in which a different event could have had an impact on the event \(A\). For example, the event \(A\) might be that “the object is at position \(x=x_1\) at time \(t=t_1\)”, so that the past light cone corresponds to the only locations in space-time that the object could have been in the past. Similarly, the future light-cone defines the locations in space-time upon which the event \(A\) could have an effect. For example, this could define the possible locations of the object in the future. The regions outside the light cones can never have an effect on the event \(A\); they are not causally connected. A signal or object would need to travel faster than the speed of light in order to have an effect on something outside of its light cone. There are locations in space-time, in the future of our Universe, that we cannot influence, no matter what we do.
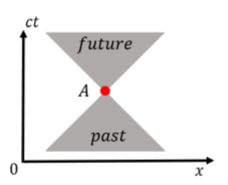
When two events in space-time are within each other’s light cones, we say that the space-time interval between them (the line that you draw from one event to the other) is “time-like”. Time-like events are such that all observers, in any frame of reference, will agree that one event happened before the other. Thus, events that are causally related must have a time-like interval between them (they are connected by a line that makes an angle greater than \(45^{\circ}\) with the horizontal axis).
Two events that are outside of each other’s light cones are said to be “space-like”. Events that are connected by space-like intervals cannot be causally related (one cannot cause the other). Observers in different frames of reference will disagree on the time ordering of space-like events. For example, when Alice observed the two clocks on the platform to emit pulses of light at the same time, Brice disagreed; those two events are connected by a space-like interval.
Finally, the space-time interval between events that are on each other’s light-cone (connected by a line that makes a \(45^{\circ}\) angle with the x-axis), is said to be “light-like” or “null”.
Lorentz transformations
In this section, we consider how to transform the space-time coordinates, \((x,y,z,ct)\), as measured in a frame of reference, \(S\), to coordinate \((x',y',z',c't)\), as measured in a frame of reference, \(S'\), that is moving with a constant speed, \(v\), relative to the frame, \(S\). For simplicity, we assume that frame \(S'\) is moving with speed \(v\) in the positive \(x\) direction, as measured in frame, \(S\), and that the origin of the two coordinate systems coincided at time \(t=0\). Figure \(\PageIndex{3}\) shows an illustration of how the two frames of reference are related (note that these are actual coordinate systems, not space-time diagrams).
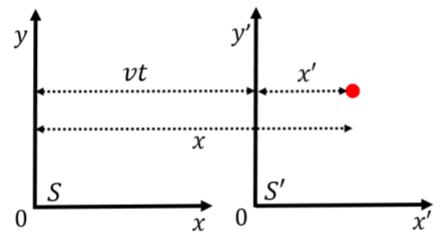
If we ignore any of Special Relativity, then the coordinates in \(S'\) are easily related to those in the \(S\) frame of reference using the “Galilean transformations”:
\[\begin{aligned} x' &= x - vt\\[4pt] y' &= y\\[4pt] z' &= z\\[4pt] t' &= t\end{aligned}\]
and this corresponds to transformations that we have implicitly used before considering Special Relativity. These equations also allow us to relate the speeds measured in different frames of reference. Suppose that an object has a velocity, \(\vec u=(u_x,u_y,u_z)\), as measured in the frame of reference, \(S\). We can obtain the components of the velocity vector, \(\vec u'\), as measured in the frame of reference, \(S'\), by taking the time derivatives of the above equations:
\[\begin{aligned} u'_x &= \frac{dx'}{dt'}=\frac{dx'}{dt}=\frac{d}{dt}(x-vt)=\frac{dx}{dt}-v=u_x - v\\[4pt] u'_y &=\frac{dy'}{dt'}=u_y\\[4pt] u'_z &=\frac{dz'}{dt'}=u_z\end{aligned}\]
which is trivial, since \(t=t'\). The transformation above are equivalent (identical) to the rules for transforming velocity that we derived in Section 3.4 for kinematics. In Galilean relativity, time is an absolute quantity that does not depend on the frame of reference. In Special Relativity, the time coordinate is different between different frames of reference, so we cannot simply convert a time derivative in \(t'\) to a derivative in \(t\). Instead, we must use the Lorentz transformations.
We can use the formulas for length contraction and time dilation to derive the Lorentz Transformations. Referring to Figure \(\PageIndex{3}\), \(x\) refers to the distance between a point in space-time and the origin of the \(x\) axis in the frame, \(S\), as measured in frame, \(S\). Similarly, \(x'\), is the distance to the point in space-time as measured in frame \(S'\), from the origin of \(S'\). In frame, \(S\), the distance \(x'\) will be contracted to the length \(x'/\gamma\), so that the Galilean transformation for the \(x\) coordinate is modified as follows:
\[\begin{aligned} x' &= x - vt\quad\text{(Galilean)}\\[4pt] \frac{x'}{\gamma} &= x - vt\\[4pt] \therefore x'&=\gamma (x-vt)\quad\text{(Lorentz)}\end{aligned}\]
The \(y\) and \(z\) coordinates are the same between frames of references, since all of the length contraction will take place in the direction of the relative motion between frames of reference, which we chose to be in the \(x\) direction.
We can obtain the equation for the time coordinate by considering that, in the \(S'\) frame of reference, it is the \(x\) coordinate that is contracted to \(x/\gamma\). In the \(S'\) frame of reference, the distance between the origins of the two systems is \(vt'\) (note the prime on \(t\)). We can thus write the contracted distance \(x\), in the \(S'\) frame of reference:
\[\begin{aligned} \frac{x}{\gamma}&=vt'+x'\\[4pt] t'&= \frac{1}{v}\left(\frac{x}{\gamma}-x'\right)\end{aligned}\]
We can eliminate \(x'\) from the last equation using the Lorentz transformation for \(x'\) that we just found:
\[\begin{aligned} t'&= \frac{1}{v}\left(\frac{x}{\gamma}-x'\right)\\[4pt] t'&= \frac{1}{v}\left(\frac{x}{\gamma}-\gamma x+\gamma vt\right)\\[4pt] \frac{t'}{\gamma}&=\frac{1}{v}\left(\frac{x}{\gamma^2}-x+vt\right)\\[4pt] &=\frac{1}{v}\left(x\left(1-\frac{v^2}{c^2}\right)-x+vt\right)\\[4pt] &=\frac{1}{v}\left(-\frac{v^2}{c^2}x+vt\right)\\[4pt] &=t-\frac{vx}{c^2}\\[4pt] \therefore t'&=\gamma\left(t-\frac{vx}{c^2} \right)\end{aligned}\]
where we wrote out the \(\gamma\) factor out explicitly in the fourth line. We can summarize the Lorentz transformations as follows:
\[\begin{aligned} x' &=\gamma (x-vt)\\[4pt] y' &= y\\[4pt] z' &= z\\[4pt] t' &=\gamma\left(t-\frac{vx}{c^2} \right)\end{aligned}\]
and the inverse relations are easily found:
\[\begin{aligned} x &=\gamma (x'+vt')\\[4pt] y &= y'\\[4pt] z &= z'\\[4pt] t &=\gamma\left(t'+\frac{vx'}{c^2} \right)\end{aligned}\]
Note that the Lorentz transformations reduce to the Galilean transformations when the speed, \(v\), between frames of reference is small (so that \(\gamma \sim 1\)).
In a frame, \(S\), a pulse of light is emitted (at the speed of light) in the positive \(x\) direction, at \(t=0\), from the origin. The pulse is then absorbed at time \(t\), at position \(x=d\). Use the Lorentz transformation to show that, in a frame, \(S'\), moving in the positive \(x\) direction with speed \(v\), relative to \(S\), the pulse also traveled at the speed of light.
Solution
In order to use the Lorentz transformations, we need to define “events”, with coordinates in space-time, that we can then convert from one frame of reference to another. Let \(A\) be the event that corresponds to the emission of the pulse of light, and \(B\) the event that corresponds to the absorption of the pulse. In frame, \(S\), the coordinates of these events are:
\[\begin{aligned} x_A&=0\\[4pt] t_A&=0\\[4pt] x_B&=d\\[4pt] t_B&=\frac{d}{c}\end{aligned}\]
where in the last line, we used the fact that, in frame, \(S\), the pulse travels at the speed of light. Applying the Lorentz transformations, we can find the coordinates of the same events in frame, \(S'\):
\[\begin{aligned} x'_A&=\gamma (x_A-vt_A)=0\\[4pt] t'_A&=\gamma\left(t_A-\frac{vx_A}{c^2} \right)=0\\[4pt] x'_B&=\gamma (x_B-vt_B)=\gamma \left(d-v\frac{d}{c}\right)\\[4pt] t'_B&=\gamma\left(t_B-\frac{vx_B}{c^2} \right)=\gamma\left(\frac{d}{c}-\frac{vd}{c^2} \right)\end{aligned}\]
The speed, \(v'_p\), of the pulse of light in frame, \(S'\), is given by:
\[\begin{aligned} v'_p&=\frac{(x'_B-x'_A)}{(t'_B-t'_A)}=\frac{\gamma \left(d-v\frac{d}{c}\right)}{\gamma\left(\frac{d}{c}-\frac{vd}{c^2} \right)}\\[4pt] &=\frac{\left(d-v\frac{d}{c}\right)}{\left(\frac{d}{c}-\frac{vd}{c^2} \right)}=c\frac{\left(\frac{d}{c}-v\frac{d}{c^2}\right)}{\left(\frac{d}{c}-\frac{vd}{c^2} \right)}=c\end{aligned}\]
which is the speed of light, as expected.
Discussion
In this example, we showed how to use the Lorentz transformations, by clearly defining “events” and their coordinates in space-time. We saw that the Lorentz transformation are consistent with Einstein’s second postulate and that the speed of light is the same all frames of reference. This of course makes sense, as we derived the Lorentz transformations from time dilation and length contraction, which are consequences of the postulate.
Einstein’s second postulate states that the speed of light is independent of the frame of reference. Consider two points in space-time corresponding to the emission (\(A\)) and the absorption (\(B\)) of a pulse of light. In the reference frame, \(S\), the distance squared in space between these two events must be equal to the distance (squared) that light traveled between the time of emission and absorption:
\[\begin{aligned} (x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2&= c^2(t_B-t_A)^2\\[4pt] \therefore \Delta x^2 + \Delta y^2 +\Delta z^2&=c^2\Delta t^2\end{aligned}\]
where \((x_A,y_A,z_A,ct_A)\) and \((x_B,y_B,z_B,ct_B)\) are the space-time coordinates of events \(A\) and \(B\). The above equation must hold in all frame of references (e.g. adding a prime to each coordinate), since it is a statement that the speed of light is \(c\).
We can define, \(s\), the ”space-time interval”, between events, \(A\) and \(B\):
\[\begin{aligned} s^2 = \Delta x^2 + \Delta y^2 +\Delta z^2&-c^2\Delta t^2\end{aligned}\]
which turns out to be “Lorentz invariant” (meaning that this value is the same in all reference frames). The space-time interval can be thought of as a “distance” in space-time that is the same in all reference frames. If the events \(A\) and \(B\) corresponds to the emission and absorption of light, then \(s=0\), and we say that the interval between \(A\) and \(B\) is light-like or null. If \(s<0\), the events are on a time-like interval, and if \(s>0\), the events are separated by a space-like interval. Since \(s\) does not depend on the frame of reference, all observers will agree on whether events are separated by time or space-like intervals.
We can visualize the effect of Lorentz transformations on space-time diagrams, as in Figure \(\PageIndex{4}\), which shows the space-time diagrams for a reference frame, \(S\), and a second reference frame, \(S'\), moving with speed \(v\) in the \(x\) direction relative to \(S\).
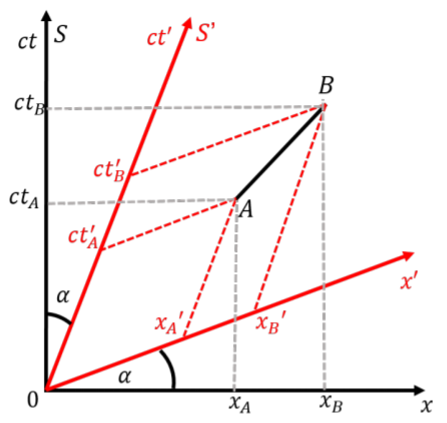
The effect of the Lorentz transformation on a space-time diagram is to tilt both the space and time axes “inwards”1, by an angle, \(\alpha\), given by:
\[\begin{aligned} \tan\alpha = \frac{v}{c}\end{aligned}\]
Figure \(\PageIndex{4}\) shows a light-like interval between two points, \(A\) and \(B\), and how to determine the space-time coordinates in the two reference frames. You can think of space-time as the sheet of paper on which events happen. You can then draw different coordinate systems on that piece of paper to describe the position (in space and time) of different events.
Use a space-time diagram to show how two events at different locations that are simultaneous in one frame of reference are not simultaneous in a reference frame that is moving relative to the one where the events are simultaneous. This is an illustration of the relativity of simultaneity that we uncovered at the beginning of the chapter when examining Alice on a train platform and the two pulses of light.
Solution
Let \(S\) be the frame of reference where events, \(A\) and \(B\), are simultaneous. These events are connected by a space-like interval, since they are separated in space, but not in time. There is no way for one event to have caused the other. In the frame, \(S\), these events are on a horizontal line in a space-time diagram.
Let us define a second reference frame, \(S'\), that is moving with speed \(v\), relative to \(S\). We have illustrated space-time diagrams for the the two reference frames, and the events \(A\) and \(B\), in Figure \(\PageIndex{5}\).
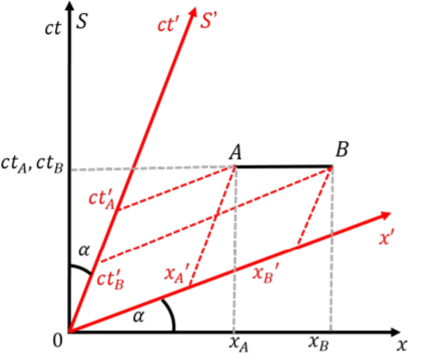
From the space-time diagram, it is clear that, in the frame of reference, \(S'\), the event \(B\) happened first. If the frame of reference \(S'\) was moving in the opposite (negative \(x\)) direction, event \(A\) would occur first, and the axes of \(S'\) would be tilted in the other direction (so that the opening angle between the axes is greater than \(90^{\circ}\)).
Discussion
This example illustrates how space-time diagrams can be used to qualitatively model events in space-time between two different reference frames. In particular, we showed how two events that are simultaneous in one frame (\(S\)) are not simultaneous in a different frame. For events connected by space-like intervals, there exist frames of reference where the events are simultaneous, or where either one happened first. If two events are separated by a time-like interval, there is no frame of reference in which one will disagree in the ordering of the events (although observers in different frames of reference will still measure different lengths of time between events due to time-dilation). For time-like events, the moving frame of reference would have to go faster than the speed of light for the time ordering to be different. This would violate causality, and is a good argument as to why nothing can go faster than the speed of light!
This chapter is where the bubble of intuitive reality is popped, and students (like you and me) are given the oppourtunity to challenge our understanding of how the universe operates. As amazing and exciting as this is, it can also be incredibly frustrating. Many students rely on intuition to guide them as they problem solve, but hit a wall in special relativity. To avoid this issue, I suggest drawing spacetime diagrams and using Lorentz transformations. Practicing with these tools will help make the process of understanding the strange consequences of Einstein’s postulates less awkward.
In addition to the practical advice I have given, I reccommend embracing the strangeness of reality. Throughout history, scientists have ventured into the unknown in attemps to discover and decode the universe. In many cases, the answer to a question has posed more questions than answers, and humanity is given the oppourunity to further understand the world we live in. As a student, you are participating in a process of understanding which allows us to continue the adventure that is scientific inquiry. Confusion can be frustrating, but don’t let it discourage you, being confused means that you’re only a few steps away from understanding!
Lorentz addition of velocities
In the previous section, we reviewed the Galilean velocity transformations, that allow us to convert a velocity, \(\vec u\), as measured in one frame of reference, to a velocity, \(\vec u'\), measured in a different frame of reference. We now derive the equivalent relations based on the Lorentz transformation. Again, we assume that frame, \(S'\), moves in the positive \(x\) direction with speed, \(v\), relative to frame, \(S\).
The \(x\) component of the velocity vector, \(\vec u'\), for some object in the \(S'\) frame of reference is given by:
\[\begin{aligned} u'_x = \frac{d}{dt'} x'\end{aligned}\]
In Galilean relativity, we could simply replace the derivative over \(t'\) by a derivative over \(t\), since the two are equivalent. This is no longer the case. However, we can use the Chain Rule and the Lorentz transformations to convert a derivative over \(t'\) to a derivative over \(t\):
\[\begin{aligned} \frac{d}{dt'} &= \frac{dt}{dt'}\frac{d}{dt}\\[4pt] &= \frac{d}{dt'} \gamma\left(t'+\frac{vx'}{c^2} \right)\frac{d}{dt}\\[4pt] &=\gamma \left(1+\frac{v}{c^2}\frac{dx'}{dt'}\right)\frac{d}{dt}\\[4pt] &=\gamma \left(1+\frac{vu'_x}{c^2}\right)\frac{d}{dt}\end{aligned}\]
where we recognized that \(\frac{dx'}{dt'}=u'_x\). The \(x\) component of the velocity, as measured in the \(S'\) frame of reference, is then given by:
\[\begin{aligned} u'_x &= \frac{d}{dt'} x' = \gamma \left(1+\frac{vu'_x}{c^2}\right)\frac{d}{dt}x'\\[4pt] &=\gamma \left(1+\frac{vu'_x}{c^2}\right)\frac{d}{dt}\gamma (x-vt)\\[4pt] &=\gamma^2 \left(1+\frac{vu'_x}{c^2}\right)(u_x -v)\\[4pt] \frac{u'_x}{\gamma^2}&=u_x -v +\frac{vu'_xu_x}{c^2}-\frac{v^2u'_x}{c^2}\\[4pt] u'_x\left (1-\frac{v^2}{c^2}\right)&=u_x -v +\frac{vu'_xu_x}{c^2}-\frac{v^2u'_x}{c^2}\\[4pt] u'_x \left( 1- \frac{vu_x}{c^2}\right) &=u_x -v \end{aligned}\]
\[\therefore\mu_{x}^{'}=\frac{\mu_{x}-v}{1-\frac{v\mu_{x}}{c^{2}}}\]
where we made use of the Lorentz transformation: \(x'=\gamma (x-vt)\). We can proceed in a similar way to determine the \(y\) and \(z\) components. Note that, unlike the Galilean case, all of the velocity components must transform, since the time derivative is involved for each component. Intuitively, we expect all components of velocity to be affected, since one needs to guarantee that the total speed is always below \(c\). The velocity transformations for all components are given by the following:
\[\begin{aligned} u'_x&=\frac{u_x -v}{1- \frac{vu_x}{c^2}}\\[4pt] u'_y &=\frac{u_y}{\gamma\left(1- \frac{vu_x}{c^2}\right)}\\[4pt] u'_z &=\frac{u_z}{\gamma\left(1- \frac{vu_x}{c^2}\right)}\end{aligned}\]
and the reverse transformations are given by:
\[\begin{aligned} u_x &=\frac{u'_x +v}{1+ \frac{vu_x}{c^2}}\\[4pt] u_y &=\frac{u'_y}{\gamma\left(1+ \frac{vu_x}{c^2}\right)}\\[4pt] u_z &=\frac{u'_z}{\gamma\left(1+ \frac{vu_x}{c^2}\right)}\end{aligned}\]
An archer can shoot a very fast arrow with a speed of \(0.5c\). The archer is on a train moving with speed, \(v=0.7c\), and fires an arrow in the direction of motion. What is the speed of the arrow, as measured in the frame of reference of the ground?
Solution
Let the train be the frame of reference, \(S'\), moving in the positive \(x\) direction with speed \(v=0.7c\) relative to the frame, \(S\), which corresponds to the ground. The speed of the arrow, as seen from the train (\(S'\)), is given by:
\[\begin{aligned} u'_x = 0.5c\end{aligned}\]
The speed of the arrow, as measured from the ground, is thus given by:
\[\begin{aligned} u_x &=\frac{u'_x +v}{1+ \frac{vu_x}{c^2}}\\[4pt] &=\frac{(0.5c) +(0.7c)}{1+ \frac{(0.7c)(0.5c)}{c^2}}\\[4pt]` &=\frac{(1.2c)}{1+(0.7)(0.5)}=\frac{1.2}{1.35}c=0.89c\end{aligned}\]
Discussion
By using the Lorentz transformations for velocity, we see that the arrow does not exceed the speed of light. Had we used Galilean relativity, we would have concluded that the arrow has a speed of \(1.2c\) when measured from the ground.
Footnotes
1. Outwards if the speed of \(S'\) is in the negative \(x\) direction relative to \(S\).