16.E: Waves (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
16.1 Traveling Waves
- Give one example of a transverse wave and one example of a longitudinal wave, being careful to note the relative directions of the disturbance and wave propagation in each.
- A sinusoidal transverse wave has a wavelength of 2.80 m. It takes 0.10 s for a portion of the string at a position x to move from a maximum position of y = 0.03 m to the equilibrium position y = 0. What are the period, frequency, and wave speed of the wave?
- What is the difference between propagation speed and the frequency of a mechanical wave? Does one or both affect wavelength? If so, how?
- Consider a stretched spring, such as a slinky. The stretched spring can support longitudinal waves and transverse waves. How can you produce transverse waves on the spring? How can you produce longitudinal waves on the spring?
- Consider a wave produced on a stretched spring by holding one end and shaking it up and down. Does the wavelength depend on the distance you move your hand up and down?
- A sinusoidal, transverse wave is produced on a stretched spring, having a period T. Each section of the spring moves perpendicular to the direction of propagation of the wave, in simple harmonic motion with an amplitude A. Does each section oscillate with the same period as the wave or a different period? If the amplitude of the transverse wave were doubled but the period stays the same, would your answer be the same?
- An electromagnetic wave, such as light, does not require a medium. Can you think of an example that would support this claim?
16.2 Mathematics of Waves
- If you were to shake the end of a taut spring up and down 10 times a second, what would be the frequency and the period of the sinusoidal wave produced on the spring?
- If you shake the end of a stretched spring up and down with a frequency f, you can produce a sinusoidal, transverse wave propagating down the spring. Does the wave number depend on the frequency you are shaking the spring?
- Does the vertical speed of a segment of a horizontal taut string through which a sinusoidal, transverse wave is propagating depend on the wave speed of the transverse wave?
- In this section, we have considered waves that move at a constant wave speed. Does the medium accelerate?
- If you drop a pebble in a pond you may notice that several concentric ripples are produced, not just a single ripple. Why do you think that is?
16.3 Wave Speed on a Stretched String
- If the tension in a string were increased by a factor of four, by what factor would the wave speed of a wave on the string increase?
- Does a sound wave move faster in seawater or fresh water, if both the sea water and fresh water are at the same temperature and the sound wave moves near the surface?ρw≈1000kg/m3,ρs≈1030kg/m3,Bw=2.15×109Pa,Bs=2.34×109Pa
- Guitars have strings of different linear mass density. If the lowest density string and the highest density string are under the same tension, which string would support waves with the higher wave speed?
- Shown below are three waves that were sent down a string at different times. The tension in the string remains constant. (a) Rank the waves from the smallest wavelength to the largest wavelength. (b) Rank the waves from the lowest frequency to the highest frequency.

- Electrical power lines connected by two utility poles are sometimes heard to hum when driven into oscillation by the wind. The speed of the waves on the power lines depend on the tension. What provides the tension in the power lines?
- Two strings, one with a low mass density and one with a high linear density are spliced together. The higher density end is tied to a lab post and a student holds the free end of the low-mass density string. The student gives the string a flip and sends a pulse down the strings. If the tension is the same in both strings, does the pulse travel at the same wave velocity in both strings? If not, where does it travel faster, in the low density string or the high density string?
16.4 Energy and Power of a Wave
- Consider a string with under tension with a constant linear mass density. A sinusoidal wave with an angular frequency and amplitude produced by some external driving force. If the frequency of the driving force is decreased to half of the original frequency, how is the time-averaged power of the wave affected? If the amplitude of the driving force is decreased by half, how is the time-averaged power affected? Explain your answer.
- Circular water waves decrease in amplitude as they move away from where a rock is dropped. Explain why.
- In a transverse wave on a string, the motion of the string is perpendicular to the motion of the wave. If this is so, how is possible to move energy along the length of the string?
- The energy from the sun warms the portion of the earth facing the sun during the daylight hours. Why are the North and South Poles cold while the equator is quite warm?
- The intensity of a spherical waves decreases as the wave moves away from the source. If the intensity of the wave at the source is I0, how far from the source will the intensity decrease by a factor of nine?
16.5 Interference of Waves
- An incident sinusoidal wave is sent along a string that is fixed to the wall with a wave speed of v. The wave reflects off the end of the string. Describe the reflected wave.
- A string of a length of 2.00 m with a linear mass density of μ = 0.006 kg/m is attached to the end of a 2.00-m-long string with a linear mass density of μ = 0.012 kg/m. The free end of the higher-density string is fixed to the wall, and a student holds the free end of the low-density string, keeping the tension constant in both strings. The student sends a pulse down the string. Describe what happens at the interface between the two strings.
- A long, tight spring is held by two students, one student holding each end. Each student gives the end a flip sending one wavelength of a sinusoidal wave down the spring in opposite directions. When the waves meet in the middle, what does the wave look like?
- Many of the topics discussed in this chapter are useful beyond the topics of mechanical waves. It is hard to conceive of a mechanical wave with sharp corners, but you could encounter such a wave form in your digital electronics class, as shown below. This could be a signal from a device known as an analog to digital converter, in which a continuous voltage signal is converted into a discrete signal or a digital recording of sound. What is the result of the superposition of the two signals?
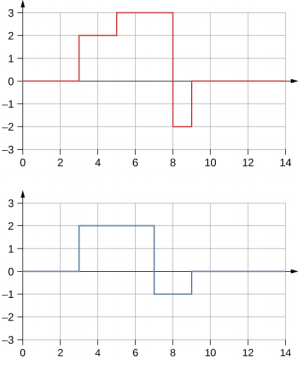
- A string of a constant linear mass density is held taut by two students, each holding one end. The tension in the string is constant. The students each send waves down the string by wiggling the string. (a) Is it possible for the waves to have different wave speeds? (b) Is it possible for the waves to have different frequencies? (c) Is it possible for the waves to have different wavelengths?
16.6 Standing Waves and Resonance
- A truck manufacturer finds that a strut in the engine is failing prematurely. A sound engineer determines that the strut resonates at the frequency of the engine and suspects that this could be the problem. What are two possible characteristics of the strut can be modified to correct the problem?
- Why do roofs of gymnasiums and churches seem to fail more than family homes when an earthquake occurs?
- Wine glasses can be set into resonance by moistening your finger and rubbing it around the rim of the glass. Why?
- Air conditioning units are sometimes placed on the roof of homes in the city. Occasionally, the air conditioners cause an undesirable hum throughout the upper floors of the homes. Why does this happen? What can be done to reduce the hum?
- Consider a standing wave modeled as y(x, t) = 4.00 cm sin (3 m−1 x) cos (4 s−1 t). Is there a node or an antinode at x = 0.00 m? What about a standing wave modeled as y(x, t) = 4.00 cm sin (3 m−1 x + π2) cos (4 s−1 t)? Is there a node or an antinode at the x = 0.00 m position?
Problems
16.1 Traveling Waves
- Storms in the South Pacific can create waves that travel all the way to the California coast, 12,000 km away. How long does it take them to travel this distance if they travel at 15.0 m/s?
- Waves on a swimming pool propagate at 0.75 m/s. You splash the water at one end of the pool and observe the wave go to the opposite end, reflect, and return in 30.00 s. How far away is the other end of the pool?
- Wind gusts create ripples on the ocean that have a wavelength of 5.00 cm and propagate at 2.00 m/s. What is their frequency?
- How many times a minute does a boat bob up and down on ocean waves that have a wavelength of 40.0 m and a propagation speed of 5.00 m/s?
- Scouts at a camp shake the rope bridge they have just crossed and observe the wave crests to be 8.00 m apart. If they shake the bridge twice per second, what is the propagation speed of the waves?
- What is the wavelength of the waves you create in a swimming pool if you splash your hand at a rate of 2.00 Hz and the waves propagate at a wave speed of 0.800 m/s?
- What is the wavelength of an earthquake that shakes you with a frequency of 10.0 Hz and gets to another city 84.0 km away in 12.0 s?
- Radio waves transmitted through empty space at the speed of light (v = c = 3.00 x 108 m/s) by the Voyager spacecraft have a wavelength of 0.120 m. What is their frequency?
- Your ear is capable of differentiating sounds that arrive at each ear just 0.34 ms apart, which is useful in determining where low frequency sound is originating from. (a) Suppose a low-frequency sound source is placed to the right of a person, whose ears are approximately 18 cm apart, and the speed of sound generated is 340 m/s. How long is the interval between when the sound arrives at the right ear and the sound arrives at the left ear? (b) Assume the same person was scuba diving and a low-frequency sound source was to the right of the scuba diver. How long is the interval between when the sound arrives at the right ear and the sound arrives at the left ear, if the speed of sound in water is 1500 m/s? (c) What is significant about the time interval of the two situations?
- (a) Seismographs measure the arrival times of earthquakes with a precision of 0.100 s. To get the distance to the epicenter of the quake, geologists compare the arrival times of S- and P-waves, which travel at different speeds. If S- and P-waves travel at 4.00 and 7.20 km/s, respectively, in the region considered, how precisely can the distance to the source of the earthquake be determined? (b) Seismic waves from underground detonations of nuclear bombs can be used to locate the test site and detect violations of test bans. Discuss whether your answer to (a) implies a serious limit to such detection. (Note also that the uncertainty is greater if there is an uncertainty in the propagation speeds of the S- and P-waves.)
- A Girl Scout is taking a 10.00-km hike to earn a merit badge. While on the hike, she sees a cliff some distance away. She wishes to estimate the time required to walk to the cliff. She knows that the speed of sound is approximately 343 meters per second. She yells and finds that the echo returns after approximately 2.00 seconds. If she can hike 1.00 km in 10 minutes, how long would it take her to reach the cliff?
- A quality assurance engineer at a frying pan company is asked to qualify a new line of nonstick-coated frying pans. The coating needs to be 1.00 mm thick. One method to test the thickness is for the engineer to pick a percentage of the pans manufactured, strip off the coating, and measure the thickness using a micrometer. This method is a destructive testing method. Instead, the engineer decides that every frying pan will be tested using a nondestructive method. An ultrasonic transducer is used that produces sound waves with a frequency of f = 25 kHz. The sound waves are sent through the coating and are reflected by the interface between the coating and the metal pan, and the time is recorded. The wavelength of the ultrasonic waves in the coating is 0.076 m. What should be the time recorded if the coating is the correct thickness (1.00 mm)?
16.2 Mathematics of Waves
- A pulse can be described as a single wave disturbance that moves through a medium. Consider a pulse that is defined at time t = 0.00 s by the equation y(x) = 6.00m3x2+2.00m2 centered around x = 0.00 m. The pulse moves with a velocity of v = 3.00 m/s in the positive x-direction. (a) What is the amplitude of the pulse? (b) What is the equation of the pulse as a function of position and time? (c) Where is the pulse centered at time t = 5.00 s ?
- A transverse wave on a string is modeled with the wave function y(x, t) = (0.20 cm) sin(2.00 m−1 x − 3.00 s−1 t + π16). What is the height of the string with respect to the equilibrium position at a position x = 4.00 m and a time t = 10.00 s?
- Consider the wave function y(x, t) = (3.00 cm) sin(0.4 m−1 x + 2.00 s−1 t + π10). What are the period, wavelength, speed, and initial phase shift of the wave modeled by the wave function?
- A pulse is defined as y(x, t) = e−2.77(2.00(x−2.00m/s(t))5.00m)2. Use a spreadsheet, or other computer program, to plot the pulse as the height of medium y as a function of position x. Plot the pulse at times t = 0.00 s and t = 3.00 s on the same graph. Where is the pulse centered at time t = 3.00 s ? Use your spreadsheet to check your answer.
- A wave is modeled at time t = 0.00 s with a wave function that depends on position. The equation is y(x) = (0.30 m) sin(6.28 m−1 x). The wave travels a distance of 4.00 meters in 0.50 s in the positive x-direction. Write an equation for the wave as a function of position and time.
- A wave is modeled with the function y(x, t) = (0.25 m) cos(0.30 m−1 x − 0.90 s−1 t + π3). Find the (a) amplitude, (b) wave number, (c) angular frequency, (d) wave speed, (e) initial phase shift, (f) wavelength, and (g) period of the wave.
- A surface ocean wave has an amplitude of 0.60 m and the distance from trough to trough is 8.00 m. It moves at a constant wave speed of 1.50 m/s propagating in the positive x-direction. At t = 0, the water displacement at x = 0 is zero, and vy is positive. (a) Assuming the wave can be modeled as a sine wave, write a wave function to model the wave. (b) Use a spreadsheet to plot the wave function at times t = 0.00 s and t = 2.00 s on the same graph. Verify that the wave moves 3.00 m in those 2.00 s.
- A wave is modeled by the wave function y(x, t) = (0.30 m) sin[2π4.50m(x−18.00m/st)]. What are the amplitude, wavelength, wave speed, period, and frequency of the wave?
- A transverse wave on a string is described with the wave function y(x, t) = (0.50 cm) sin(1.57 m−1 x − 6.28 s−1 t). (a) What is the wave velocity of the wave? (b) What is the magnitude of the maximum velocity of the string perpendicular to the direction of the motion?
- A swimmer in the ocean observes one day that the ocean surface waves are periodic and resemble a sine wave. The swimmer estimates that the vertical distance between the crest and the trough of each wave is approximately 0.45 m, and the distance between each crest is approximately 1.8 m. The swimmer counts that 12 waves pass every two minutes. Determine the simple harmonic wave function that would describes these waves.
- Consider a wave described by the wave function y(x, t) = 0.3 m sin(2.00 m−1 x − 628.00 s−1 t). (a) How many crests pass by an observer at a fixed location in 2.00 minutes? (b) How far has the wave traveled in that time?
- Consider two waves defined by the wave functions y1(x, t) = 0.50 m sin(2π3.00mx+2π4.00st) and y2(x, t) = 0.50 m sin(2π6.00mx−2π4.00st). What are the similarities and differences between the two waves?
- Consider two waves defined by the wave functions y1(x, t) = 0.20 m sin(2π6.00mx−2π4.00st) and y2(x, t) = 0.20 m cos(2π6.00mx−2π4.00st). What are the similarities and differences between the two waves?
- The speed of a transverse wave on a string is 300.00 m/s, its wavelength is 0.50 m, and the amplitude is 20.00 cm. How much time is required for a particle on the string to move through a distance of 5.00 km?
16.3 Wave Speed on a Stretched String
- Transverse waves are sent along a 5.00-m-long string with a speed of 30.00 m/s. The string is under a tension of 10.00 N. What is the mass of the string?
- A copper wire has a density of ρ = 8920 kg/m3, a radius of 1.20 mm, and a length L. The wire is held under a tension of 10.00 N. Transverse waves are sent down the wire. (a) What is the linear mass density of the wire? (b) What is the speed of the waves through the wire?
- A piano wire has a linear mass density of μ = 4.95 x 10−3 kg/m. Under what tension must the string be kept to produce waves with a wave speed of 500.00 m/s?
- A string with a linear mass density of μ = 0.0060 kg/m is tied to the ceiling. A 20-kg mass is tied to the free end of the string. The string is plucked, sending a pulse down the string. Estimate the speed of the pulse as it moves down the string.
- A cord has a linear mass density of μ = 0.0075 kg/m and a length of three meters. The cord is plucked and it takes 0.20 s for the pulse to reach the end of the string. What is the tension of the string?
- A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
- A sound wave travels through a column of nitrogen at STP. Assuming a density of ρ = 1.25 kg/m3 and a bulk modulus of β = 1.42 x 105 Pa, what is the approximate speed of the sound wave?
- What is the approximate speed of sound traveling through air at a temperature of T = 28°C ?
- Transverse waves travel through a string where the tension equals 7.00 N with a speed of 20.00 m/s. What tension would be required for a wave speed of 25.00 m/s?
- Two strings are attached between two poles separated by a distance of 2.00 m as shown below, both under the same tension of 600.00 N. String 1 has a linear density of μ1 = 0.0025 kg/m and string 2 has a linear mass density of μ2 = 0.0035 kg/m. Transverse wave pulses are generated simultaneously at opposite ends of the strings. How much time passes before the pulses pass one another?
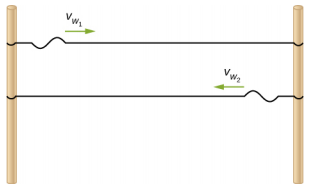
- Two strings are attached between two poles separated by a distance of 2.00 meters as shown in the preceding figure, both strings have a linear density of μ1 = 0.0025 kg/m, the tension in string 1 is 600.00 N and the tension in string 2 is 700.00 N. Transverse wave pulses are generated simultaneously at opposite ends of the strings. How much time passes before the pulses pass one another?
- The note E4 is played on a piano and has a frequency of f = 393.88. If the linear mass density of this string of the piano is μ = 0.012 kg/m and the string is under a tension of 1000.00 N, what is the speed of the wave on the string and the wavelength of the wave?
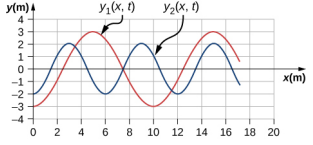
- Two transverse waves travel through a taut string. The speed of each wave is v = 30.00 m/s. A plot of the vertical position as a function of the horizontal position is shown below for the time t = 0.00 s. (a) What is the wavelength of each wave? (b) What is the frequency of each wave? (c) What is the maximum vertical speed of each string?
- A sinusoidal wave travels down a taut, horizontal string with a linear mass density of µ = 0.060 kg/m . The maximum vertical speed of the wave is vy max = 0.30 cm/s. The wave is modeled with the wave equation y(x, t) = A sin(6.00 m−1 x − 24.00 s−1 t) . (a) What is the amplitude of the wave? (b) What is the tension in the string?
- The speed of a transverse wave on a string is v = 60.00 m/s and the tension in the string is FT = 100.00 N . What must the tension be to increase the speed of the wave to v = 120.00 m/s?
16.4 Energy and Power of a Wave
- A string of length 5 m and a mass of 90 g is held under a tension of 100 N. A wave travels down the string that is modeled as y(x, t) = 0.01 m sin(15.7 m−1 x − 1170.12 s−1). What is the power over one wavelength?
- Ultrasound of intensity 1.50 x 102 W/m2 is produced by the rectangular head of a medical imaging device measuring 3.00 cm by 5.00 cm. What is its power output?
- The low-frequency speaker of a stereo set has a surface area of A = 0.05 m2 and produces 1 W of acoustical power. (a) What is the intensity at the speaker? (b) If the speaker projects sound uniformly in all directions, at what distance from the speaker is the intensity 0.1 W/m2?
- To increase the intensity of a wave by a factor of 50, by what factor should the amplitude be increased?
- A device called an insolation meter is used to measure the intensity of sunlight. It has an area of 100 cm2 and registers 6.50 W. What is the intensity in W/m2 ?
- Energy from the Sun arrives at the top of Earth’s atmosphere with an intensity of 1400 W/m2. How long does it take for 1.80 x 109 J to arrive on an area of 1.00 m2?
- Suppose you have a device that extracts energy from ocean breakers in direct proportion to their intensity. If the device produces 10.0 kW of power on a day when the breakers are 1.20 m high, how much will it produce when they are 0.600 m high?
- A photovoltaic array of (solar cells) is 10.0% efficient in gathering solar energy and converting it to electricity. If the average intensity of sunlight on one day is 70.00 W/m2, what area should your array have to gather energy at the rate of 100 W? (b) What is the maximum cost of the array if it must pay for itself in two years of operation averaging 10.0 hours per day? Assume that it earns money at the rate of 9.00 cents per kilowatt-hour.
- A microphone receiving a pure sound tone feeds an oscilloscope, producing a wave on its screen. If the sound intensity is originally 2.00 x 10−5 W/m2, but is turned up until the amplitude increases by 30.0%, what is the new intensity?
- A string with a mass of 0.30 kg has a length of 4.00 m. If the tension in the string is 50.00 N, and a sinusoidal wave with an amplitude of 2.00 cm is induced on the string, what must the frequency be for an average power of 100.00 W?
- The power versus time for a point on a string (μ = 0.05 kg/m) in which a sinusoidal traveling wave is induced is shown in the preceding figure. The wave is modeled with the wave equation y(x, t) = A sin(20.93 m−1 x − ωt). What is the frequency and amplitude of the wave?
- A string is under tension FT1. Energy is transmitted by a wave on the string at rate P1 by a wave of frequency f1. What is the ratio of the new energy transmission rate P2 to P1 if the tension is doubled?
- A 250-Hz tuning fork is struck and the intensity at the source is I1 at a distance of one meter from the source. (a) What is the intensity at a distance of 4.00 m from the source? (b) How far from the tuning fork is the intensity a tenth of the intensity at the source? 88. A sound speaker is rated at a voltage of P = 120.00 V and a current of I = 10.00 A. Electrical power consumption is P = IV. To test the speaker, a signal of a sine wave is applied to the speaker. Assuming that the sound wave moves as a spherical wave and that all of the energy applied to the speaker is converted to sound energy, how far from the speaker is the intensity equal to 3.82 W/m2?
- The energy of a ripple on a pond is proportional to the amplitude squared. If the amplitude of the ripple is 0.1 cm at a distance from the source of 6.00 meters, what was the amplitude at a distance of 2.00 meters from the source?
16.5 Interference of Waves
- Consider two sinusoidal waves traveling along a string, modeled as y1(x, t) = 0.3 m sin(4 m−1 x + 3 s−1 t) and y2(x, t) = 0.6 m sin(8 m−1 x − 6 s−1 t). What is the height of the resultant wave formed by the interference of the two waves at the position x = 0.5 m at time t = 0.2 s?
- Consider two sinusoidal sine waves traveling along a string, modeled as y1(x, t) = 0.3 m sin(4 m−1 x + 3 s−1 t + π3) and y2(x, t) = 0.6 m sin(8 m−1 x − 6 s−1 t). What is the height of the resultant wave formed by the interference of the two waves at the position x = 1.0 m at time t = 3.0 s?
- Consider two sinusoidal sine waves traveling along a string, modeled as y1(x, t) = 0.3 m sin(4 m−1 x − 3 s−1 t) and y2(x, t) = 0.3 m sin(4 m−1 x + 3 s−1 t). What is the wave function of the resulting wave? [Hint: Use the trig identity sin(u ± v) = sin u cos v ± cos u sin v]
- Two sinusoidal waves are moving through a medium in the same direction, both having amplitudes of 3.00 cm, a wavelength of 5.20 m, and a period of 6.52 s, but one has a phase shift of an angle ϕ. What is the phase shift if the resultant wave has an amplitude of 5.00 cm? [Hint: Use the trig identity sin u + sin v = 2 sin(u+v2) cos(u−v2)]
- Two sinusoidal waves are moving through a medium in the positive x-direction, both having amplitudes of 6.00 cm, a wavelength of 4.3 m, and a period of 6.00 s, but one has a phase shift of an angle ϕ = 0.50 rad. What is the height of the resultant wave at a time t = 3.15 s and a position x = 0.45 m?
- Two sinusoidal waves are moving through a medium in the positive x-direction, both having amplitudes of 7.00 cm, a wave number of k = 3.00 m−1 , an angular frequency of ω = 2.50 s−1, and a period of 6.00 s, but one has a phase shift of an angle ϕ = π12 rad. What is the height of the resultant wave at a time t = 2.00 s and a position x = 0.53 m?
- Consider two waves y1(x, t) and y2(x, t) that are identical except for a phase shift propagating in the same medium. (a) What is the phase shift, in radians, if the amplitude of the resulting wave is 1.75 times the amplitude of the individual waves? (b) What is the phase shift in degrees? (c) What is the phase shift as a percentage of the individual wavelength?
- Two sinusoidal waves, which are identical except for a phase shift, travel along in the same direction. The wave equation of the resultant wave is yR(x, t) = 0.70 m sin(3.00 m−1 x − 6.28 s−1 t + π16 rad). What are the angular frequency, wave number, amplitude, and phase shift of the individual waves?
- Two sinusoidal waves, which are identical except for a phase shift, travel along in the same direction. The wave equation of the resultant wave is yR(x, t) = 0.35 cm sin(6.28 m−1 x − 1.57 s−1 t + π4). What are the period, wavelength, amplitude, and phase shift of the individual waves?
- Consider two wave functions, y1(x, t) = 4.00 m sin(π m−1 x − π s−1 t) and y2(x, t) = 4.00 m sin(π m−1 x − π s−1 t + π3). (a) Using a spreadsheet, plot the two wave functions and the wave that results from the superposition of the two wave functions as a function of position (0.00 ≤ x ≤ 6.00 m) for the time t = 0.00 s. (b) What are the wavelength and amplitude of the two original waves? (c) What are the wavelength and amplitude of the resulting wave?
- Consider two wave functions, y2(x, t) = 2.00 m sin(π2 m−1 x − π3 s−1 t) and y2(x, t) = 2.00 m sin(π2 m−1 x − π3 s−1 t + π6). (a) Verify that yR= 2A cos(ϕ2) sin(kx − ωt + ϕ2) is the solution for the wave that results from a superposition of the two waves. Make a column for x, y1, y2, y1 + y2, and yR = 2A cos(ϕ2) sin(kx − ωt + ϕ2). Plot four waves as a function of position where the range of x is from 0 to 12 m.
- Consider two wave functions that differ only by a phase shift, y1(x, t) = A cos(kx − ωt) and y2(x, t) = A cos(kx − ωt + ϕ). Use the trigonometric identities cos u + cos v = 2 cos(u−v2) cos (u+v2) and cos(−θ) = cos(θ) to find a wave equation for the wave resulting from the superposition of the two waves. Does the resulting wave function come as a surprise to you?
16.6 Standing Waves and Resonance
- A wave traveling on a Slinky® that is stretched to 4 m takes 2.4 s to travel the length of the Slinky and back again. (a) What is the speed of the wave? (b) Using the same Slinky stretched to the same length, a standing wave is created which consists of three antinodes and four nodes. At what frequency must the Slinky be oscillating?
- A 2-m long string is stretched between two supports with a tension that produces a wave speed equal to vw = 50.00 m/s. What are the wavelength and frequency of the first three modes that resonate on the string?
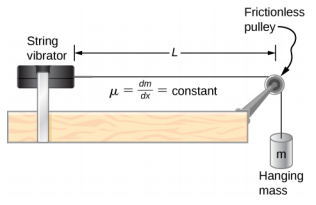
- Consider the experimental setup shown below. The length of the string between the string vibrator and the pulley is L = 1.00 m. The linear density of the string is μ = 0.006 kg/m. The string vibrator can oscillate at any frequency. The hanging mass is 2.00 kg. (a)What are the wavelength and frequency of n = 6 mode? (b) The string oscillates the air around the string. What is the wavelength of the sound if the speed of the sound is vs = 343.00 m/s?
- A cable with a linear density of μ = 0.2 kg/m is hung from telephone poles. The tension in the cable is 500.00 N. The distance between poles is 20 meters. The wind blows across the line, causing the cable resonate. A standing waves pattern is produced that has 4.5 wavelengths between the two poles. The speed of sound at the current temperature T = 20 °C is 343.00 m/s. What are the frequency and wavelength of the hum?
- Consider a rod of length L, mounted in the center to a support. A node must exist where the rod is mounted on a support, as shown below. Draw the first two normal modes of the rod as it is driven into resonance. Label the wavelength and the frequency required to drive the rod into resonance.
- Consider two wave functions y(x, t) = 0.30 cm sin(3 m−1 x − 4 s−1 t) and y(x, t) = 0.30 cm sin(3 m−1 x + 4 s−1 t). Write a wave function for the resulting standing wave.
- A 2.40-m wire has a mass of 7.50 g and is under a tension of 160 N. The wire is held rigidly at both ends and set into oscillation. (a) What is the speed of waves on the wire? The string is driven into resonance by a frequency that produces a standing wave with a wavelength equal to 1.20 m. (b) What is the frequency used to drive the string into resonance?
- A string with a linear mass density of 0.0062 kg/m and a length of 3.00 m is set into the n = 100 mode of resonance. The tension in the string is 20.00 N. What is the wavelength and frequency of the wave?
- A string with a linear mass density of 0.0075 kg/m and a length of 6.00 m is set into the n = 4 mode of resonance by driving with a frequency of 100.00 Hz. What is the tension in the string?
- Two sinusoidal waves with identical wavelengths and amplitudes travel in opposite directions along a string producing a standing wave. The linear mass density of the string is μ = 0.075 kg/m and the tension in the string is FT = 5.00 N. The time interval between instances of total destructive interference is Δt = 0.13 s. What is the wavelength of the waves?
- A string, fixed on both ends, is 5.00 m long and has a mass of 0.15 kg. The tension if the string is 90 N. The string is vibrating to produce a standing wave at the fundamental frequency of the string. (a) What is the speed of the waves on the string? (b) What is the wavelength of the standing wave produced? (c) What is the period of the standing wave?
- A string is fixed at both end. The mass of the string is 0.0090 kg and the length is 3.00 m. The string is under a tension of 200.00 N. The string is driven by a variable frequency source to produce standing waves on the string. Find the wavelengths and frequency of the first four modes of standing waves.
- The frequencies of two successive modes of standing waves on a string are 258.36 Hz and 301.42 Hz. What is the next frequency above 100.00 Hz that would produce a standing wave?
- A string is fixed at both ends to supports 3.50 m apart and has a linear mass density of μ = 0.005 kg/m. The string is under a tension of 90.00 N. A standing wave is produced on the string with six nodes and five antinodes. What are the wave speed, wavelength, frequency, and period of the standing wave?
- Sine waves are sent down a 1.5-m-long string fixed at both ends. The waves reflect back in the opposite direction. The amplitude of the wave is 4.00 cm. The propagation velocity of the waves is 175 m/s. The n = 6 resonance mode of the string is produced. Write an equation for the resulting standing wave.
Additional Problems
- Ultrasound equipment used in the medical profession uses sound waves of a frequency above the range of human hearing. If the frequency of the sound produced by the ultrasound machine is f = 30 kHz, what is the wavelength of the ultrasound in bone, if the speed of sound in bone is v = 3000 m/s?
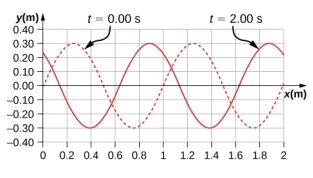
- Shown below is the plot of a wave function that models a wave at time t = 0.00 s and t = 2.00 s. The dotted line is the wave function at time t = 0.00 s and the solid line is the function at time t = 2.00 s. Estimate the amplitude, wavelength, velocity, and period of the wave.
- The speed of light in air is approximately v = 3.00 x 108 m/s and the speed of light in glass is v = 2.00 x 108 m/s. A red laser with a wavelength of λ = 633.00 nm shines light incident of the glass, and some of the red light is transmitted to the glass. The frequency of the light is the same for the air and the glass. (a) What is the frequency of the light? (b) What is the wavelength of the light in the glass?
- A radio station broadcasts radio waves at a frequency of 101.7 MHz. The radio waves move through the air at approximately the speed of light in a vacuum. What is the wavelength of the radio waves?
- A sunbather stands waist deep in the ocean and observes that six crests of periodic surface waves pass each minute. The crests are 16.00 meters apart. What is the wavelength, frequency, period, and speed of the waves?
- A tuning fork vibrates producing sound at a frequency of 512 Hz. The speed of sound of sound in air is v = 343.00 m/s if the air is at a temperature of 20.00 °C. What is the wavelength of the sound?
- A motorboat is traveling across a lake at a speed of vb = 15.00 m/s. The boat bounces up and down every 0.50 s as it travels in the same direction as a wave. It bounces up and down every 0.30 s as it travels in a direction opposite the direction of the waves. What is the speed and wavelength of the wave?
- Use the linear wave equation to show that the wave speed of a wave modeled with the wave function y(x, t) = 0.20 m sin(3.00 m−1 x + 6.00 s−1 t) is v = 2.00 m/s. What are the wavelength and the speed of the wave?
- Given the wave functions y1(x, t) = A sin(kx − ωt) and y2(x, t) = A sin(kx − ωt + ϕ) with ϕ≠π2, show that y1(x, t) + y2(x, t) is a solution to the linear wave equation with a wave velocity of v = ωk.
- A transverse wave on a string is modeled with the wave function y(x, t) = 0.10 m sin(0.15 m−1 x + 1.50 s−1 t + 0.20). (a) Find the wave velocity. (b) Find the position in the y-direction, the velocity perpendicular to the motion of the wave, and the acceleration perpendicular to the motion of the wave, of a small segment of the string centered at x = 0.40 m at time t = 5.00 s.
- A sinusoidal wave travels down a taut, horizontal string with a linear mass density of μ = 0.060 kg/m. The magnitude of maximum vertical acceleration of the wave is ay max = 0.90 cm/s2 and the amplitude of the wave is 0.40 m. The string is under a tension of FT = 600.00 N . The wave moves in the negative x-direction. Write an equation to model the wave.
- A transverse wave on a string (μ = 0.0030 kg/m) is described with the equation y(x, t) = 0.30 m sin(2π4.00m(x−16.00m/st)). What is the tension under which the string is held taut?
- A transverse wave on a horizontal string (μ = 0.0060 kg/m) is described with the equation y(x, t) = 0.30 m sin(2π4.00m(x−vwt)). The string is under a tension of 300.00 N. What are the wave speed, wave number, and angular frequency of the wave?
- A student holds an inexpensive sonic range finder and uses the range finder to find the distance to the wall. The sonic range finder emits a sound wave. The sound wave reflects off the wall and returns to the range finder. The round trip takes 0.012 s. The range finder was calibrated for use at room temperature T = 20 °C, but the temperature in the room is actually T = 23 °C. Assuming that the timing mechanism is perfect, what percentage of error can the student expect due to the calibration?
- A wave on a string is driven by a string vibrator, which oscillates at a frequency of 100.00 Hz and an amplitude of 1.00 cm. The string vibrator operates at a voltage of 12.00 V and a current of 0.20 A. The power consumed by the string vibrator is P = IV. Assume that the string vibrator is 90% efficient at converting electrical energy into the energy associated with the vibrations of the string. The string is 3.00 m long, and is under a tension of 60.00 N. What is the linear mass density of the string?
- A traveling wave on a string is modeled by the wave equation y(x, t) = 3.00 cm sin(8.00 m−1 x + 100.00 s−1 t). The string is under a tension of 50.00 N and has a linear mass density of μ = 0.008 kg/m. What is the average power transferred by the wave on the string?
- A transverse wave on a string has a wavelength of 5.0 m, a period of 0.02 s, and an amplitude of 1.5 cm. The average power transferred by the wave is 5.00 W. What is the tension in the string?
- (a) What is the intensity of a laser beam used to burn away cancerous tissue that, when 90.0% absorbed, puts 500 J of energy into a circular spot 2.00 mm in diameter in 4.00 s? (b) Discuss how this intensity compares to the average intensity of sunlight (about) and the implications that would have if the laser beam entered your eye. Note how your answer depends on the time duration of the exposure.
- Consider two periodic wave functions, y1(x, t) = A sin(kx − ωt) and y2(x, t) = A sin(kx − ωt + ϕ). (a) For what values of ϕ will the wave that results from a superposition of the wave functions have an amplitude of 2A? (b) For what values of ϕ will the wave that results from a superposition of the wave functions have an amplitude of zero?
- Consider two periodic wave functions, y1(x, t) = A sin(kx − ωt) and y2(x, t) = A cos(kx − ωt + ϕ). (a) For what values of ϕ will the wave that results from a superposition of the wave functions have an amplitude of 2A? (b) For what values of ϕ will the wave that results from a superposition of the wave functions have an amplitude of zero?
- A trough with dimensions 10.00 meters by 0.10 meters by 0.10 meters is partially filled with water. Small-amplitude surface water waves are produced from both ends of the trough by paddles oscillating in simple harmonic motion. The height of the water waves are modeled with two sinusoidal wave equations, y1(x, t) = 0.3 m sin(4 m−1 x − 3 s−1 t) and y2 (x, t) = 0.3 m cos(4 m−1 x + 3 s−1 t − π2). What is the wave function of the resulting wave after the waves reach one another and before they reach the end of the trough (i.e., assume that there are only two waves in the trough and ignore reflections)? Use a spreadsheet to check your results. [Hint: Use the trig identities sin(u ± v) = sin u cos v ± cos u sin v and cos(u ± v) = cos u cos v ∓ sin u sin v]
- A seismograph records the S- and P-waves from an earthquake 20.00 s apart. If they traveled the same path at constant wave speeds of vS = 4.00 km/s and vP = 7.50 km/s, how far away is the epicenter of the earthquake?
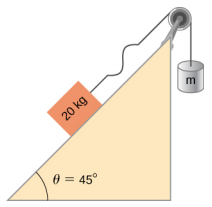
- Consider what is shown below. A 20.00-kg mass rests on a frictionless ramp inclined at 45°. A string with a linear mass density of μ = 0.025 kg/m is attached to the 20.00-kg mass. The string passes over a frictionless pulley of negligible mass and is attached to a hanging mass (m). The system is in static equilibrium. A wave is induced on the string and travels up the ramp. (a) What is the mass of the hanging mass (m)? (b) At what wave speed does the wave travel up the string?
- Consider the superposition of three wave functions y(x, t) = 3.00 cm sin(2 m−1 x − 3 s−1 t), y(x, t) = 3.00 cm sin(6 m−1 x + 3 s−1 t), and y(x, t) = 3.00 cm sin(2 m−1 x − 4 s−1 t). What is the height of the resulting wave at position x = 3.00 m at time t = 10.0 s?
- A string has a mass of 150 g and a length of 3.4 m. One end of the string is fixed to a lab stand and the other is attached to a spring with a spring constant of ks = 100 N/m. The free end of the spring is attached to another lab pole. The tension in the string is maintained by the spring. The lab poles are separated by a distance that stretches the spring 2.00 cm. The string is plucked and a pulse travels along the string. What is the propagation speed of the pulse?
- A standing wave is produced on a string under a tension of 70.0 N by two sinusoidal transverse waves that are identical, but moving in opposite directions. The string is fixed at x = 0.00 m and x = 10.00 m. Nodes appear at x = 0.00 m, 2.00 m, 4.00 m, 6.00 m, 8.00 m, and 10.00 m. The amplitude of the standing wave is 3.00 cm. It takes 0.10 s for the antinodes to make one complete oscillation. (a) What are the wave functions of the two sine waves that produce the standing wave? (b) What are the maximum velocity and acceleration of the string, perpendicular to the direction of motion of the transverse waves, at the antinodes?
- A string with a length of 4 m is held under a constant tension. The string has a linear mass density of μ = 0.006 kg/m. Two resonant frequencies of the string are 400 Hz and 480 Hz. There are no resonant frequencies between the two frequencies. (a) What are the wavelengths of the two resonant modes? (b) What is the tension in the string?
Challenge Problems
- A copper wire has a radius of 200 μm and a length of 5.0 m. The wire is placed under a tension of 3000 N and the wire stretches by a small amount. The wire is plucked and a pulse travels down the wire. What is the propagation speed of the pulse? (Assume the temperature does not change: (ρ = 8.96 g/cm3, Y = 1.1 x 1011 N/m).
- A pulse moving along the x axis can be modeled as the wave function y(x, t) = 4.00 m e−(x+(2.00m/s)t1.00m)2. (a) What are the direction and propagation speed of the pulse? (b) How far has the wave moved in 3.00 s? (c) Plot the pulse using a spreadsheet at time t = 0.00 s and t = 3.00 s to verify your answer in part (b).
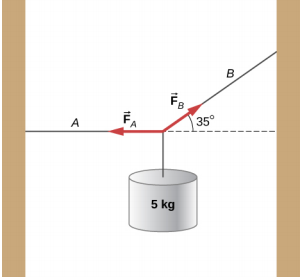
- A string with a linear mass density of μ = 0.0085 kg/m is fixed at both ends. A 5.0-kg mass is hung from the string, as shown below. If a pulse is sent along section A, what is the wave speed in section A and the wave speed in section B?
- Consider two wave functions y1(x, t) = A sin(kx − ωt) and y2(x, t) = A sin(kx + ωt + ϕ). What is the wave function resulting from the interference of the two wave? [Hint: sin(α±β) = sin α cos β ± cos α sin β and ϕ=ϕ2+ϕ2).
- The wave function that models a standing wave is given as yR (x, t) = 6.00 cm sin(3.00 m−1 x + 1.20 rad) cos(6.00 s−1 t + 1.20 rad). What are two wave functions that interfere to form this wave function? Plot the two wave functions and the sum of the sum of the two wave functions at t = 1.00 s to verify your answer.
- Consider two wave functions y1(x, t) = A sin(kx − ωt) and y2(x, t) = A sin(kx + ωt + ϕ). The resultant wave form when you add the two functions is yR = 2A sin(kx + ϕ2) cos(\omega t + \frac{\phi}{2}\)). Consider the case where A = 0.03 m−1, k = 1.26 m−1, ω=π s−1, and ϕ=π10. (a) Where are the first three nodes of the standing wave function starting at zero and moving in the positive x direction? (b) Using a spreadsheet, plot the two wave functions and the resulting function at time t = 1.00 s to verify your answer.


