19.4: Complex Atoms

Last updated
Save as PDF

Page ID: 32867

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The energy levels of the hydrogen atom whose energies are given by equation (19.3.8) are actually degenerate, in that each energy has more than one state associated with it. Three extra degrees of freedom are associated with angular momentum, expressed by the quantum numbers l, m, and m_s. For energy level n, the orbital angular momentum quantum number can take on the values \(l=0,1,2, \ldots, n-1\). Thus, for the ground state, n = 1, the only possible value of \(l\) is zero. For a given value of \(l\), there are \(2l+ 1\) possible values of the orbital z component quantum number, \(m = -l,-l + 1,…,l\). Finally, there are two possible values of the spin orientation quantum number, \(\mathrm{m}_{\mathrm{S}}\). Thus, for the nth energy level there are

\[N_{n}=2 \sum_{l=0}^{n-1}(2 l+1)\label{19.15}\]

states. In particular, for \(\mathrm{n}=1,2,3, \ldots\), we have \(\mathrm{N}_{n}=2,8,18, \ldots\). This is summarized in figure 19.2.

Figure 19.2: Energy levels of the hydrogen atom. Energy increases upward and angular momentum increases to the right. The numbers above each level indicate the spin orientation multiplied by the orbital orientation degeneracy for each level. The numbers at the right show the total degeneracy for each value of n. Only the first three values of n are shown.

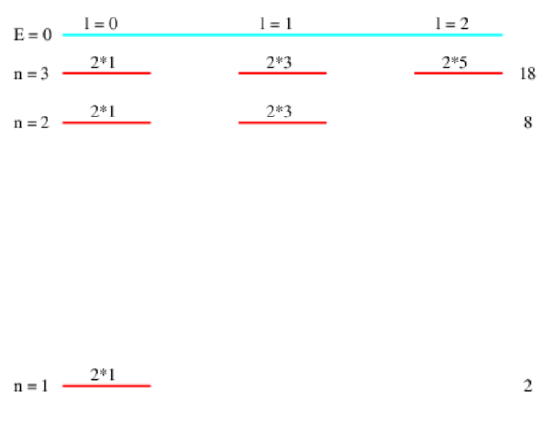
These results have implications for the character of atoms with more than one proton in the nucleus. Let us imagine how such atoms might be built. The binding energy of a single electron in the ground state of a nucleus with \(Z\) protons is \(Z^{2}\) multiplied by the binding energy of the electron in the ground state of a hydrogen atom. If the force between electrons can be ignored compared to the force between an electron and the nucleus (a very poor but initially useful assumption that we will discuss below), then we could construct an atom by dropping \(Z\) electrons one by one into the potential well of the nucleus. The Pauli exclusion principle prevents all of these electrons from falling into the ground state. Instead, the available states will fill in order of lowest energy first until all \(Z\) electrons are added and the atom becomes electrically neutral. From figure 19.2 we see that \(Z = 2\) fills the \(n = 1\) levels with two electrons, one spin up and one spin down, both with zero orbital angular momentum. For \(Z = 10\) the \(n = 2\) levels fill such that two electrons have \(l = 0\) and six have \(l = 1\).

As electrons are added to an atom, previous electrons tend to shield subsequent electrons from the nucleus, since their negative charge partially compensates for the nuclear positive charge. Thus, binding energies are considerably less than would be expected on the basis of the non-interacting electron model. Furthermore, the binding energies for states with higher orbital angular momentum are smaller than those with lower values, since electrons in these states tend to be more effectively shielded from the nucleus by other electrons. This effect becomes sufficiently important at higher \(Z\) to disrupt the sequence in which states are filled by electrons — sometimes level \(n + 1\) states with low \(l\) start to fill before all the level \(n\) states with large \(l\) are full. Accurate calculations of atomic properties in which electron-electron interactions are taken into account are possible, but are computationally expensive.