19.6: Problems

Last updated
Save as PDF

Page ID: 32869

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The wave function for three non-identical particles in a box of unit length with one particle in the ground state, the second in the first excited state, and the third in the second excited state is \(\psi\left(x_{1}, x_{2}, x_{3}\right)=\sin \left(\pi x_{1}\right) \sin \left(2 \pi x_{2}\right) \sin \left(3 \pi x_{3}\right) .\)
Hint: In each case there are six terms corresponding to the six permutations of \(x_{1}, x_{2}, \text { and } x_{3}\). Exchanging any two particles leaves \(\Psi\) unchanged for bosons but changes the sign for fermions.
1. From this write down the wave function for three identical bosons in the above mentioned states.
2. Do the same for three identical fermions.
Two identical particles with equal energies collide nearly head-on, so that they are both deflected through an angle \(\theta\), as shown in figure 19.4. A physicist calculates the amplitude \(\Psi\) as a function of \(\theta\) for this deflection to take place (using very advanced theory!), resulting in the solid curve shown in figure 19.4. However, measurements show that the actual amplitude as a function of \(\theta\) (not probability!) is given by the dashed curve.
Hint: If the outgoing particles (but not the incoming particles) are interchanged, how does the apparent deflection angle change?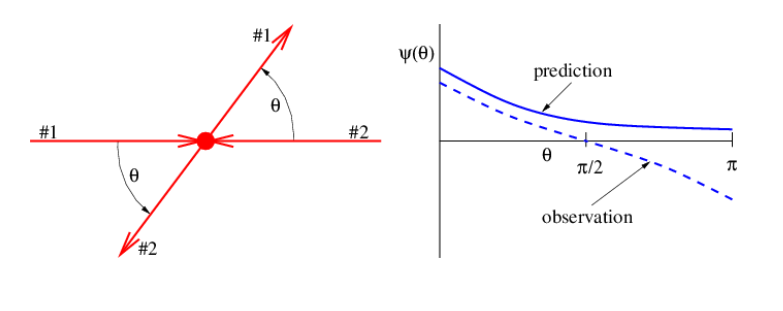Figure 19.4: Incorrectly calculated and observed scattering amplitude for a collision between two identical particles.
1. What did the physicist forget to take into account? Explain.
2. Are the particles fermions or bosons? Explain.
Consider the hydrogen atom, which has one electron circling the nucleus.
1. Suppose that the electron moves in a circle of radius R with velocity v, as shown in figure 19.5. (This can only occur in an excited state of the atom.) Use Ampére’s law to estimate the magnetic field produced at the nucleus. Hint: Derive an equation for the average magnetic field over a magnetic circulation loop of radius R that circles the trajectory of the electron. Assume that the field at the nucleus is somewhat greater than this average value. (Pick a number.)
2. The radius of the hydrogen atom in an excited state is of order 10^-10 m. Compute the orbital velocity of the electron for a circular orbit, given the electron mass and the charges on the electron and the proton nucleus.
3. From the above information compute an approximate value for the magnetic field at the nucleus caused by the electron’s orbital motion. 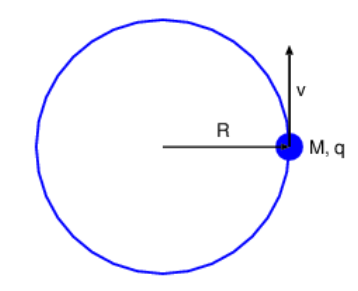Figure 19.5: Charge of mass \(M\) and charge \(q\) moving in a circle of radius \(R\) at speed \(v\).
4. The Stern-Gerlach experiment demonstrated the quantization of angular momentum by passing a beam of neutral silver atoms (approximately 108 times the mass of a proton) through a magnetic field with a strong gradient. (See figure 19.6.) Since silver has one unpaired electron, the magnetic dipole moment is non-zero. Assuming a vertical gradient in the vertical component of the magnetic field, the silver atoms will be deflected either up or down, depending on the orientation of the dipole moment.
  1. For a given value of \(\partial \mathrm{B}_{\mathrm{z}} / \partial \mathrm{z}\), derive an expression for the \(z\) component of the force on a silver atom, assuming that the dipole moment equals one Bohr magneton aligned (1) in the \(+z\) and (2) in the \(-z\) directions.
  2. If the silver atom has mass \(M\) and initial speed \(v\), compute the angular deflection up or down of the trajectory of the silver atom as it passes through the field of the magnet, assumed to have length \(L\).
  3. Assuming \(\partial B_{z} / \partial z=10^{2} T / m, v=300 m / s, \text { and } L=10 \mathrm{~cm}\) compute the above deflection angle.
  4. Explain why the classical result is different from the quantum result as illustrated in figure 19.6.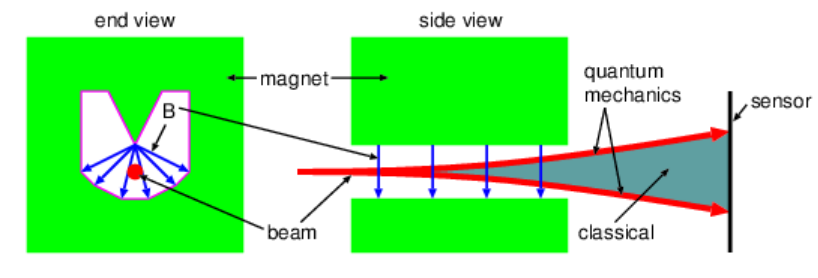Figure 19.6: Stern-Gerlach experiment. A neutral silver atom moves through a non-uniform magnetic field and is deflected according to the orientation of its magnetic moment vector.
5. Following the analysis made for the hydrogen atom, compute the “Bohr radius” and the ground state binding energy for an “atom” consisting of Z protons in the nucleus and one electron.
6. Upper and lower bounds on the binding energy of the last (outermost) electron in the sodium atom \(Z = 11\) may be obtained by assuming (a) that the other electrons have no effect, or (b) that the other electrons neutralize all but one proton in the nucleus. Compute the binding energy of the last electron in sodium in these two limits. (The actual binding energy of the last electron in sodium is \(5.139 eV.\))
7. A uranium atom \(Z = 92\) has all its electrons stripped off except the first one.
  1. What is the first electron’s binding energy in electron volts?
  2. What is the ground state radius of the electron orbit in this case?
8. The energy levels of a particle in a box are given by \(E_{n}=E_{0} n^{2}=E_{0}, 4 E_{0}, 9 E_{0}, \ldots\) where \(\mathrm{E}_{0}\) is the ground state energy for the particle. Find the lowest possible total energy of a group of particles, expressed as a multiple of \(\mathrm{E}_{0}\), for the following particles in the box:
  1. 5 identical spin 0 particles.
  2. 5 identical spin 1/2 particles.
  3. 5 identical spin 1 particles.
  4. 5 identical spin 3/2 particles.
9. A charged particle in a 1-D box has energy levels at \(\mathrm{E}_{\mathrm{n}}=\mathrm{E}_{0} \mathrm{n}^{2}=\mathrm{E}_{0}, 4 \mathrm{E}_{0}, 9 \mathrm{E}_{0}, 16 \mathrm{E}_{0}, 25 \mathrm{E}_{0, \ldots}\) where \(\mathrm{E}_{0}\) is the ground state energy of the particle. If the particle can absorb a photon with any of the energies \(5 \mathrm{E}_{0,} 12 \mathrm{E}_{0}, 21 \mathrm{E}_{0},...\), what can you infer about the initial energy of the particle? Explain.
10. The X-rays in your dentist’s office are produced when an energetic beam of free electrons knocks the most tightly bound electrons \(n = 1\) completely out of the target atoms. Electrons from the next level up \(n = 2\) then drop into the \(n = 1\) level.
  1. Estimate the energy in electron volts of the resulting photons for a copper target \(Z = 29\). Hint: For the inner electrons, you may ignore the effects of the other electrons to reasonable accuracy.
  2. What minimum energy must the electron beam have in this case?
11. What is the shortest ultraviolet wavelength usable in astronomy? Hint: \(UV\) photons more energetic than the binding energy of the electron in hydrogen are strongly absorbed by this gas.
12. In the naive periodic table model, the first three closed shells occur for \(Z = 2, 10, 28\). However, the first three noble gases have \(Z = 2, 10, 18\). Explain why this is so.