11.4: Quarks
- Page ID
- 4557
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Compare and contrast the six known quarks
- Use quark composition of hadrons to determine the total charge of these particles
- Explain the primary evidence for the existence of quarks
In the 1960s, particle physicists began to realize that hadrons are not elementary particles but are made of particles called quarks. (The name ‘quark’ was coined by the physicist Murray Gell-Mann, from a phrase in the James Joyce novel Finnegans Wake.) Initially, it was believed there were only three types of quarks, called up (u), down (d), and strange (s). However, this number soon grew to six—interestingly, the same as the number of leptons—to include charmed (c), bottom (b), and top (t).
All quarks are spin-half fermions \((s = 1/2)\), have a fractional charge \((1/3\) or \(2/3 e)\), and have baryon number \(B = 1/3\). Each quark has an antiquark with the same mass but opposite charge and baryon number. The names and properties of the six quarks are listed in Table.
| Quark | Charge (units of e) | Spin (s) | Baryon number | Strangeness number |
|---|---|---|---|---|
| Down (d) | - 1/3 | 1/2 | 1/3 | 0 |
| Up (u) | + 2/3 | 1/2 | 1/3 | 0 |
| Strange (s) | - 1/3 | 1/2 | 1/3 | - 1 |
| Charm (c) | + 2/3 | 1/2 | 1/3 | 0 |
| Bottom (b) | - 1/3 | 1/2 | 1/3 | 0 |
| Top (t) | + 2/3 | 1/2 | 1/3 | 0 |
Quark Combinations
As mentioned earlier, quarks bind together in groups of two or three to form hadrons. Baryons are formed from three quarks. Sample baryons, including quark content and properties, are given in Table. Interestingly, the delta plus (\(\Delta^+\)) baryon is formed from the same three quarks as the proton, but the total spin of the particle is 3/2 rather than 1/2. Similarly, the mass of \(\Delta^+\) with spin 3/2 is 1.3 times the mass of the proton, and the delta zero (\(\Delta^0\)) baryon with a spin 3/2 is 1.3 times the neutron mass. Evidently, the energy associated with the spin (or angular momentum) of the particle contributes to its mass energy. It is also interesting that no baryons are believed to exist with top quarks, because top quarks decay too quickly to bind to the other quarks in their production.
| Name | Symbol | Quarks | Charge (unit of e) | Spin (s) | Mass \((GeV/c^2)\) |
|---|---|---|---|---|---|
| Proton | p | u u d | 1 | 1/2 | 0.938 |
| Neutron | n | u d d | 0 | 1/2 | 0.940 |
| Delta plus plus | \(\Delta^{++}\) | u u u | 2 | 3/2 | 1.232 |
| Delta plus | \(\Delta^+\) | u u d | 1 | 3/2 | 1.232 |
| Delta zero | \(\Delta^0\) | u d d | 0 | 3/2 | 1.232 |
| Delta minus | \(\Delta^-\) | d d d | -1 | 3/2 | 1.232 |
| Lambda zero | \(\Lambda^0\) | u d s | 0 | 1/2 | 1.116 |
| Positive sigma | \(\Sigma^+\) | u u s | 1 | 1/2 | 1.189 |
| Neutral sigma | \(\Sigma^0\) | u d s | 0 | 1/2 | 1.192 |
| Negative xi | \(\Xi^-\) | s d s | -1 | 1/2 | 1.321 |
| Neutral xi | \(\Xi_0\) | s u s | 0 | 1/2 | 1.315 |
| Omega minus | \(\Omega^-\) | s s s | -1 | 3/2 | 1.672 |
| Charmed lambda | \(\Lambda_{C+}\) | u d c | 1 | 1/2 | 2.281 |
| Charmed bottom | \(\Lambda_{b0}\) | u d b | 0 | 1/2 | 5.612 |
Mesons are formed by two quarks—a quark-antiquark pair. Sample mesons, including quark content and properties, are given in Table \(\PageIndex{3}\). Consider the formation of the pion (\(\pi^+ = u\overline{d}\)). Based on its quark content, the charge of the pion is
\[\dfrac{2}{3}e + \dfrac{1}{3}e = e. \nonumber \]
Both quarks are spin-half (\(s = \dfrac{1}{2}\)), so the resultant spin is either 0 or 1. The spin of the \((\pi^+)\) meson is 0. The same quark-antiquark combination gives the rho (\(\rho\)) meson with spin 1. This meson has a mass approximately 5.5 times that of the \(\pi^+\) meson.
Show that the quark composition given in Table \(\PageIndex{2}\) for \(\Xi^0\) is consistent with the known charge, spin, and strangeness of this baryon.
Strategy
\(\Xi^0\) is composed of two strange quarks and an up quark (s u s). We can add together the properties of quarks to predict the resulting properties of the \(\Xi^0\) baryon.
Solution
The charge of the s quark is \(-e/3\) and the charge of the u quark is 2e/3. Thus, the combination (s u s) has no net charge, in agreement with the known charge of \(\Xi^0\). Since three spin \(-1/2\) quarks can combine to produce a particle with spin of either 1/2 or 3/2, the quark composition is consistent with the known spin (\(s = 1/2\)) of \(\Xi^0\). Finally, the net strangeness of the (s u s) combination is \((-1) + 0 + (-1) = -2\), which also agrees with experiment.
Significance
The charge, spin, and strangeness of the \(\Xi^0\) particle can be determined from the properties of its constituent quarks. The great diversity of baryons and mesons can be traced to the properties of just six quarks: up, down, charge, strange, top, and bottom.
What is the baryon number of a pion?
- Answer
-
0
Color
Quarks are fermions that obey Pauli’s exclusion principle, so it might be surprising to learn that three quarks can bind together within a nucleus. For example, how can two up quarks exist in the same small region of space within a proton? The solution is to invent a third new property to distinguish them. This property is called color, and it plays the same role in the strong nuclear interaction as charge does in electromagnetic interactions. For this reason, quark color is sometimes called “strong charge.”
Quarks come in three colors: red, green, and blue. (These are just labels—quarks are not actually colored.) Each type of quark \((u, \, d, \, c, \, s, \, b, \, t)\) can possess any other colors. For example, three strange quarks exist: a red strange quark, a green strange quark, and a blue strange quark. Antiquarks have anticolor. Quarks that bind together to form hadrons (baryons and mesons) must be color neutral, colorless, or “white.” Thus, a baryon must contain a red, blue, and green quark. Likewise, a meson contains either a red-antired, blue-antiblue, or green-antigreen quark pair. Thus, two quarks can be found in the same spin state in a hadron, without violating Pauli’s exclusion principle, because their colors are different.
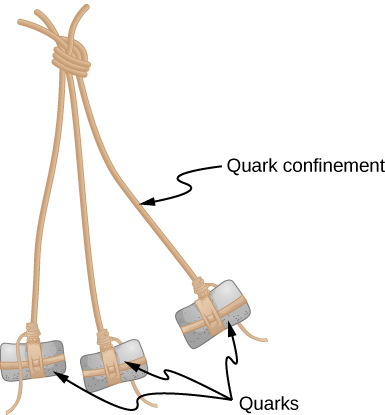
Quark Confinement
The first strong evidence for the existence of quarks came from a series of experiments performed at the Stanford Linear Accelerator Center (SLAC) and at CERN around 1970. This experiment was designed to probe the structure of the proton, much like Rutherford studied structure inside the atom with his \(\alpha\)-particle scattering experiments. Electrons were collided with protons with energy in excess of 20 GeV. At this energy, \(E \approx pc\), so the de Broglie wavelength of an electron is
\[\lambda = \dfrac{h}{p} = \dfrac{hc}{E} \approx 6 \times 10^{-17} m. \nonumber \]
The wavelength of the electron is much smaller than the diameter of the proton (about \(10^{-15} m)\). Thus, like an automobile traveling through a rocky mountain range, electrons can be used to probe the structure of the nucleus.
The SLAC experiments found that some electrons were deflected at very large angles, indicating small scattering centers within the proton. The scattering distribution was consistent with electrons being scattered from sites with spin 1/2, the spin of quarks. The experiments at CERN used neutrinos instead of electrons. This experiment also found evidence for the tiny scattering centers. In both experiments, the results suggested that the charges of the scattering particles were either \(+2/3e\) or \(-1/3 e\), in agreement with the quark model.
Watch this video to learn more about quarks.
Protons and neutrons are made of three quarks, right? Wrong! Explore the particle they should have told you about when you were a kid!
The quark model has been extremely successful in organizing the complex world of subatomic particles. Interestingly, however, no experiment has ever produced an isolated quark. All quarks have fractional charge and should therefore be easily distinguishable from the known elementary particles, whose charges are all an integer multiple of e. Why are isolated quarks not observed? In current models of particle interactions, the answer is expressed in terms of quark confinement. Quark confinement refers to the confinement of quarks in groups of two or three in a small region of space. The quarks are completely free to move about in this space, and send and receive gluons (the carriers of the strong force). However, if these quarks stray too far from one another, the strong force pulls them back it. This action is likened to a bola, a weapon used for hunting (Figure \(\PageIndex{1}\)). The stones are tied to a central point by a string, so none of the rocks can move too far from the others. The bola corresponds to a baryon, the stones correspond to quarks, and the string corresponds to the gluons that hold the system together.