8.8: Capacitance (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
8.2 Capacitors and Capacitance
1. Does the capacitance of a device depend on the applied voltage? Does the capacitance of a device depend on the charge residing on it?
2. Would you place the plates of a parallel-plate capacitor closer together or farther apart to increase their capacitance?
3. The value of the capacitance is zero if the plates are not charged. True or false?
4. If the plates of a capacitor have different areas, will they acquire the same charge when the capacitor is connected across a battery?
5. Does the capacitance of a spherical capacitor depend on which sphere is charged positively or negatively?
8.3 Capacitors in Series and in Parallel
6. If you wish to store a large amount of charge in a capacitor bank, would you connect capacitors in series or in parallel? Explain.
7. What is the maximum capacitance you can get by connecting three 1.0-μF capacitors? What is the minimum capacitance?
8.4 Energy Stored in a Capacitor
8. If you wish to store a large amount of energy in a capacitor bank, would you connect capacitors in series or parallel? Explain.
8.5 Capacitor with a Dielectric
9. Discuss what would happen if a conducting slab rather than a dielectric were inserted into the gap between the capacitor plates.
10. Discuss how the energy stored in an empty but charged capacitor changes when a dielectric is inserted if (a) the capacitor is isolated so that its charge does not change; (b) the capacitor remains connected to a battery so that the potential difference between its plates does not change.
8.6 Molecular Model of a Dielectric
11. Distinguish between dielectric strength and dielectric constant.
12. Water is a good solvent because it has a high dielectric constant. Explain.
13. Water has a high dielectric constant. Explain why it is then not used as a dielectric material in capacitors.
14. Elaborate on why molecules in a dielectric material experience net forces on them in a non-uniform electrical field but not in a uniform field.
15. Explain why the dielectric constant of a substance containing permanent molecular electric dipoles decreases with increasing temperature.
16. Give a reason why a dielectric material increases capacitance compared with what it would be with air between the plates of a capacitor. How does a dielectric material also allow a greater voltage to be applied to a capacitor? (The dielectric thus increases C and permits a greater V.)
17. Elaborate on the way in which the polar character of water molecules helps to explain water’s relatively large dielectric constant.
18. Sparks will occur between the plates of an air-filled capacitor at a lower voltage when the air is humid than when it is dry. Discuss why, considering the polar character of water molecules.
Problems
8.2 Capacitors and Capacitance
19. What charge is stored in a 180.0-μF capacitor when 120.0 V is applied to it?
20. Find the charge stored when 5.50 V is applied to an 8.00-pF capacitor.
21. Calculate the voltage applied to a 2.00-μF capacitor when it holds 3.10μC of charge.
22. What voltage must be applied to an 8.00-nF capacitor to store 0.160 mC of charge?
23. What capacitance is needed to store 3.00μC of charge at a voltage of 120 V?
24. What is the capacitance of a large Van de Graaff generator’s terminal, given that it stores 8.00 mC of charge at a voltage of 12.0 MV?
25. The plates of an empty parallel-plate capacitor of capacitance 5.0 pF are 2.0 mm apart. What is the area of each plate?
26. A 60.0-pF vacuum capacitor has a plate area of 0.010m2. What is the separation between its plates?
27. A set of parallel plates has a capacitance of 5.0µF. How much charge must be added to the plates to increase the potential difference between them by 100 V?
28. Consider Earth to be a spherical conductor of radius 6400 km and calculate its capacitance.
29. If the capacitance per unit length of a cylindrical capacitor is 20 pF/m, what is the ratio of the radii of the two cylinders?
30. An empty parallel-plate capacitor has a capacitance of 20µF. How much charge must leak off its plates before the voltage across them is reduced by 100 V?
8.3 Capacitors in Series and in Parallel
31. A 4.00-pF is connected in series with an 8.00-pF capacitor and a 400-V potential difference is applied across the pair. (a) What is the charge on each capacitor?
(b) What is the voltage across each capacitor?
32. Three capacitors, with capacitances of \displaystyle C_1=2.0μF, C_2=3.0μF, and \displaystyle C_3=6.0μF, respectively, are connected in parallel. A 500-V potential difference is applied across the combination. Determine the voltage across each capacitor and the charge on each capacitor.
33. Find the total capacitance of this combination of series and parallel capacitors shown below.
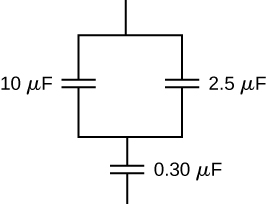
34. Suppose you need a capacitor bank with a total capacitance of 0.750 F but you have only 1.50-mF capacitors at your disposal. What is the smallest number of capacitors you could connect together to achieve your goal, and how would you connect them?
35. What total capacitances can you make by connecting a 5.00-μF and a 8.00-μF capacitor?
36. Find the equivalent capacitance of the combination of series and parallel capacitors shown below.
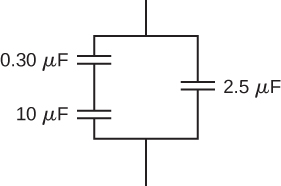
37. Find the net capacitance of the combination of series and parallel capacitors shown below.
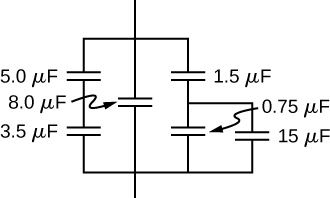
38. A 40-pF capacitor is charged to a potential difference of 500 V. Its terminals are then connected to those of an uncharged 10-pF capacitor. Calculate:
(a) the original charge on the 40-pF capacitor;
(b) the charge on each capacitor after the connection is made; and
(c) the potential difference across the plates of each capacitor after the connection.
39. A 2.0-μF capacitor and a 4.0-μF capacitor are connected in series across a 1.0-kV potential. The charged capacitors are then disconnected from the source and connected to each other with terminals of like sign together. Find the charge on each capacitor and the voltage across each capacitor.
8.4 Energy Stored in a Capacitor
40. How much energy is stored in an 8.00-μF capacitor whose plates are at a potential difference of 6.00 V?
41. A capacitor has a charge of 2.5μC when connected to a 6.0-V battery. How much energy is stored in this capacitor?
42. How much energy is stored in the electrical field of a metal sphere of radius 2.0 m that is kept at a 10.0-V potential?
43. (a) What is the energy stored in the 10.0-μF capacitor of a heart defibrillator charged to \displaystyle 9.00×10^3V?
(b) Find the amount of the stored charge.
44. In open-heart surgery, a much smaller amount of energy will defibrillate the heart.
(a) What voltage is applied to the 8.00-μF capacitor of a heart defibrillator that stores 40.0 J of energy?
(b) Find the amount of the stored charge.
45. A 165-μF capacitor is used in conjunction with a dc motor. How much energy is stored in it when 119 V is applied?
46. Suppose you have a 9.00-V battery, a 2.00-μF capacitor, and a 7.40-μF capacitor.
(a) Find the charge and energy stored if the capacitors are connected to the battery in series.
(b) Do the same for a parallel connection.
47. An anxious physicist worries that the two metal shelves of a wood frame bookcase might obtain a high voltage if charged by static electricity, perhaps produced by friction.
(a) What is the capacitance of the empty shelves if they have area \displaystyle 1.00×10^2m and are 0.200 m apart?
(b) What is the voltage between them if opposite charges of magnitude 2.00 nC are placed on them?
(c) To show that this voltage poses a small hazard, calculate the energy stored.
(d) The actual shelves have an area 100 times smaller than these hypothetical shelves. Are his fears justified?
48. A parallel-plate capacitor is made of two square plates 25 cm on a side and 1.0 mm apart. The capacitor is connected to a 50.0-V battery. With the battery still connected, the plates are pulled apart to a separation of 2.00 mm. What are the energies stored in the capacitor before and after the plates are pulled farther apart? Why does the energy decrease even though work is done in separating the plates?
49. Suppose that the capacitance of a variable capacitor can be manually changed from 100 pF to 800 pF by turning a dial, connected to one set of plates by a shaft, from 0° to 180°. With the dial set at 180°180° (corresponding to C=800pF), the capacitor is connected to a 500-V source. After charging, the capacitor is disconnected from the source, and the dial is turned to 0°. If friction is negligible, how much work is required to turn the dial from 180° to 0°?
8.5 Capacitor with a Dielectric
50. Show that for a given dielectric material, the maximum energy a parallel-plate capacitor can store is directly proportional to the volume of dielectric.
51. An air-filled capacitor is made from two flat parallel plates 1.0 mm apart. The inside area of each plate is 8.0cm28.0cm2.
(a) What is the capacitance of this set of plates?
(b) If the region between the plates is filled with a material whose dielectric constant is 6.0, what is the new capacitance?
52. A capacitor is made from two concentric spheres, one with radius 5.00 cm, the other with radius 8.00 cm.
(a) What is the capacitance of this set of conductors?
(b) If the region between the conductors is filled with a material whose dielectric constant is 6.00, what is the capacitance of the system?
53. A parallel-plate capacitor has charge of magnitude 9.00μC on each plate and capacitance 3.00μF when there is air between the plates. The plates are separated by 2.00 mm. With the charge on the plates kept constant, a dielectric with \kappa = 5 is inserted between the plates, completely filling the volume between the plates.
(a) What is the potential difference between the plates of the capacitor, before and after the dielectric has been inserted?
(b) What is the electrical field at the point midway between the plates before and after the dielectric is inserted?
54. Some cell walls in the human body have a layer of negative charge on the inside surface. Suppose that the surface charge densities are \displaystyle ±0.50×10^{−3}C/m^2, the cell wall is \displaystyle 5.0×10^{−9}m thick, and the cell wall material has a dielectric constant of κ=5.4.
(a) Find the magnitude of the electric field in the wall between two charge layers.
(b) Find the potential difference between the inside and the outside of the cell. Which is at higher potential?
(c) A typical cell in the human body has volume \displaystyle 10^{−16}m^3. Estimate the total electrical field energy stored in the wall of a cell of this size when assuming that the cell is spherical. (Hint: Calculate the volume of the cell wall.)
55. A parallel-plate capacitor with only air between its plates is charged by connecting the capacitor to a battery. The capacitor is then disconnected from the battery, without any of the charge leaving the plates.
(a) A voltmeter reads 45.0 V when placed across the capacitor. When a dielectric is inserted between the plates, completely filling the space, the voltmeter reads 11.5 V. What is the dielectric constant of the material?
(b) What will the voltmeter read if the dielectric is now pulled away out so it fills only one-third of the space between the plates?
8.6 Molecular Model of a Dielectric
56. Two flat plates containing equal and opposite charges are separated by material 4.0 mm thick with a dielectric constant of 5.0. If the electrical field in the dielectric is 1.5 MV/m, what are
(a) the charge density on the capacitor plates, and
(b) the induced charge density on the surfaces of the dielectric?
57. For a Teflon™-filled, parallel-plate capacitor, the area of the plate is \displaystyle 50.0cm^2 and the spacing between the plates is 0.50 mm. If the capacitor is connected to a 200-V battery, find
(a) the free charge on the capacitor plates,
(b) the electrical field in the dielectric, and
(c) the induced charge on the dielectric surfaces.
58. Find the capacitance of a parallel-plate capacitor having plates with a surface area of \displaystyle 5.00m^2 and separated by 0.100 mm of Teflon™.
59. (a) What is the capacitance of a parallel-plate capacitor with plates of area \displaystyle 1.50m^2 that are separated by 0.0200 mm of neoprene rubber?
(b) What charge does it hold when 9.00 V is applied to it?
60. Two parallel plates have equal and opposite charges. When the space between the plates is evacuated, the electrical field is \displaystyle E=3.20×10^5V/m. When the space is filled with dielectric, the electrical field is \displaystyle E=2.50×10^5V/m.
(a) What is the surface charge density on each surface of the dielectric?
(b) What is the dielectric constant?
61. The dielectric to be used in a parallel-plate capacitor has a dielectric constant of 3.60 and a dielectric strength of \displaystyle 1.60×10^7V/m. The capacitor has to have a capacitance of 1.25 nF and must be able to withstand a maximum potential difference 5.5 kV. What is the minimum area the plates of the capacitor may have?
62. When a 360-nF air capacitor is connected to a power supply, the energy stored in the capacitor is 18.5μJ. While the capacitor is connected to the power supply, a slab of dielectric is inserted that completely fills the space between the plates. This increases the stored energy by 23.2μJ.
(a) What is the potential difference between the capacitor plates?
(b) What is the dielectric constant of the slab?
63. A parallel-plate capacitor has square plates that are 8.00 cm on each side and 3.80 mm apart. The space between the plates is completely filled with two square slabs of dielectric, each 8.00 cm on a side and 1.90 mm thick. One slab is Pyrex glass and the other slab is polystyrene. If the potential difference between the plates is 86.0 V, find how much electrical energy can be stored in this capacitor.
Additional Problems
64. A capacitor is made from two flat parallel plates placed 0.40 mm apart. When a charge of 0.020μC is placed on the plates the potential difference between them is 250 V.
(a) What is the capacitance of the plates?
(b) What is the area of each plate?
(c) What is the charge on the plates when the potential difference between them is 500 V?
(d) What maximum potential difference can be applied between the plates so that the magnitude of electrical fields between the plates does not exceed 3.0 MV/m?
65. An air-filled (empty) parallel-plate capacitor is made from two square plates that are 25 cm on each side and 1.0 mm apart. The capacitor is connected to a 50-V battery and fully charged. It is then disconnected from the battery and its plates are pulled apart to a separation of 2.00 mm.
(a) What is the capacitance of this new capacitor?
(b) What is the charge on each plate?
(c) What is the electrical field between the plates?
66. Suppose that the capacitance of a variable capacitor can be manually changed from 100 to 800 pF by turning a dial connected to one set of plates by a shaft, from 0° to 180°. With the dial set at 180° (corresponding to C=800pF), the capacitor is connected to a 500-V source. After charging, the capacitor is disconnected from the source, and the dial is turned to 0°. (a) What is the charge on the capacitor? (b) What is the voltage across the capacitor when the dial is set to 0°?
67. Earth can be considered as a spherical capacitor with two plates, where the negative plate is the surface of Earth and the positive plate is the bottom of the ionosphere, which is located at an altitude of approximately 70 km. The potential difference between Earth’s surface and the ionosphere is about 350,000 V.
(a) Calculate the capacitance of this system.
(b) Find the total charge on this capacitor.
(c) Find the energy stored in this system.
68. A 4.00-μF capacitor and a 6.00-μF capacitor are connected in parallel across a 600-V supply line.
(a) Find the charge on each capacitor and voltage across each.
(b) The charged capacitors are disconnected from the line and from each other. They are then reconnected to each other with terminals of unlike sign together. Find the final charge on each capacitor and the voltage across each.
69. Three capacitors having capacitances of 8.40, 8.40, and 4.20 μF, respectively, are connected in series across a 36.0-V potential difference.
(a) What is the charge on the 4.20-μF capacitor?
(b) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
70. A parallel-plate capacitor with capacitance 5.0μF is charged with a 12.0-V battery, after which the battery is disconnected. Determine the minimum work required to increase the separation between the plates by a factor of 3.
71. (a) How much energy is stored in the electrical fields in the capacitors (in total) shown below?
(b) Is this energy equal to the work done by the 400-V source in charging the capacitors?
72. Three capacitors having capacitances 8.4, 8.4, and 4.2 μF are connected in series across a 36.0-V potential difference.
(a) What is the total energy stored in all three capacitors?
(b) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other with the positively charged plates connected together. What is the total energy now stored in the capacitors?
73. (a) An 8.00-μF capacitor is connected in parallel to another capacitor, producing a total capacitance of 5.00μF. What is the capacitance of the second capacitor?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
74. (a) On a particular day, it takes \displaystyle 9.60×10^3J of electrical energy to start a truck’s engine. Calculate the capacitance of a capacitor that could store that amount of energy at 12.0 V.
(b) What is unreasonable about this result?
(c) Which assumptions are responsible?
75. (a) A certain parallel-plate capacitor has plates of area \displaystyle 4.00m^2, separated by 0.0100 mm of nylon, and stores 0.170 C of charge. What is the applied voltage?
(b) What is unreasonable about this result?
(c) Which assumptions are responsible or inconsistent?
76. A prankster applies 450 V to an 80.0-μF capacitor and then tosses it to an unsuspecting victim. The victim’s finger is burned by the discharge of the capacitor through 0.200 g of flesh. Estimate, what is the temperature increase of the flesh? Is it reasonable to assume that no thermodynamic phase change happened?
Challenge Problems
77. A spherical capacitor is formed from two concentric spherical conducting spheres separated by vacuum. The inner sphere has radius 12.5 cm and the outer sphere has radius 14.8 cm. A potential difference of 120 V is applied to the capacitor.
(a) What is the capacitance of the capacitor?
(b) What is the magnitude of the electrical field at r=12.6cm, just outside the inner sphere?
(c) What is the magnitude of the electrical field at r=14.7cm, just inside the outer sphere?
(d) For a parallel-plate capacitor the electrical field is uniform in the region between the plates, except near the edges of the plates. Is this also true for a spherical capacitor?
78. The network of capacitors shown below are all uncharged when a 300-V potential is applied between points A and B with the switch S open.
(a) What is the potential difference \displaystyle V_E−V_D?
(b) What is the potential at point E after the switch is closed?
(c) How much charge flows through the switch after it is closed?
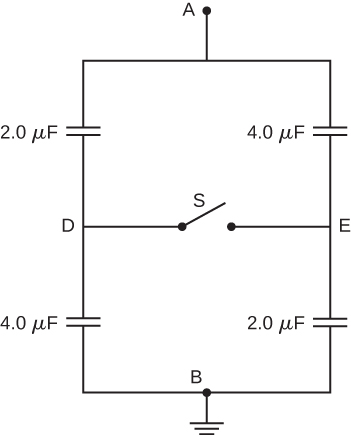
79. Electronic flash units for cameras contain a capacitor for storing the energy used to produce the flash. In one such unit the flash lasts for 1/675 fraction of a second with an average light power output of 270 kW.
(a) If the conversion of electrical energy to light is 95% efficient (because the rest of the energy goes to thermal energy), how much energy must be stored in the capacitor for one flash?
(b) The capacitor has a potential difference between its plates of 125 V when the stored energy equals the value stored in part (a). What is the capacitance?
80. A spherical capacitor is formed from two concentric spherical conducting shells separated by a vacuum. The inner sphere has radius 12.5 cm and the outer sphere has radius 14.8 cm. A potential difference of 120 V is applied to the capacitor.
(a) What is the energy density at r=12.6cm, just outside the inner sphere?
(b) What is the energy density at r=14.7cm, just inside the outer sphere?
(c) For the parallel-plate capacitor the energy density is uniform in the region between the plates, except near the edges of the plates. Is this also true for the spherical capacitor?
81. A metal plate of thickness t is held in place between two capacitor plates by plastic pegs, as shown below. The effect of the pegs on the capacitance is negligible. The area of each capacitor plate and the area of the top and bottom surfaces of the inserted plate are all A. What is the capacitance of this system?
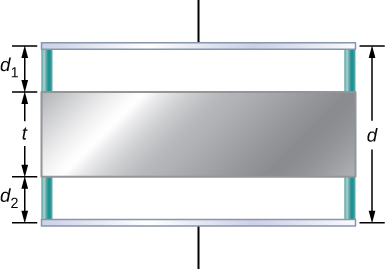
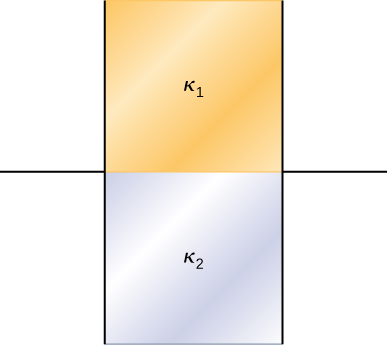
82. A parallel-plate capacitor is filled with two dielectrics, as shown below. When the plate area is A and separation between plates is d, show that the capacitance is given by \displaystyle C=ε_0\frac{A}{d}\frac{κ_1+κ_2}{2}.
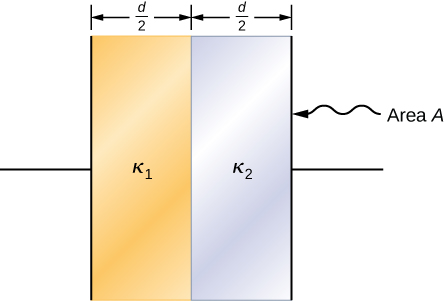
83. A parallel-plate capacitor is filled with two dielectrics, as shown below. Show that the capacitance is given by \displaystyle C=2ε_0\frac{A}{d}\frac{κ_1κ_2}{κ_1+κ_2}.
84. A capacitor has parallel plates of area \displaystyle 12cm^2 separated by 2.0 mm. The space between the plates is filled with polystyrene.
(a) Find the maximum permissible voltage across the capacitor to avoid dielectric breakdown.
(b) When the voltage equals the value found in part (a), find the surface charge density on the surface of the dielectric.


