15.6: Resonance in an AC Circuit
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of the section, you will be able to:
- Determine the peak ac resonant angular frequency for a RLC circuit
- Explain the width of the average power versus angular frequency curve and its significance using terms like bandwidth and quality factor
In the RLC series circuit of Figure 15.4.1, the current amplitude is, from Equation 15.4.7,
I_0 = \dfrac{V_0}{\sqrt{R^2 + (\omega L - 1/\omega C)^2}}. \label{15.15}
If we can vary the frequency of the ac generator while keeping the amplitude of its output voltage constant, then the current changes accordingly. A plot of I_0 versus \omega is shown in Figure \PageIndex{1}.

In Oscillations, we encountered a similar graph where the amplitude of a damped harmonic oscillator was plotted against the angular frequency of a sinusoidal driving force (see Forced Oscillations). This similarity is more than just a coincidence, as shown earlier by the application of Kirchhoff’s loop rule to the circuit of Figure 15.4.1. This yields
L\dfrac{di}{dt} + iR + \dfrac{q}{C} = V_0 \, \sin \, \omega t, \label{15.16}
or
L\dfrac{d^2q}{dt^2} + R\dfrac{dq}{dt} + \dfrac{1}{C}q = V_0 \, \sin \, \omega t, \nonumber
where we substituted dq(t)/dt for i(t). A comparison of Equation \ref{15.16} and, from Oscillations, Damped Oscillations for damped harmonic motion clearly demonstrates that the driven RLC series circuit is the electrical analog of the driven damped harmonic oscillator.
The resonant frequency f_0 of the RLC circuit is the frequency at which the amplitude of the current is a maximum and the circuit would oscillate if not driven by a voltage source. By inspection, this corresponds to the angular frequency \omega_0 = 2\pi f_0 at which the impedance Z in Equation \ref{15.15} is a minimum, or when
\omega_0 L = \dfrac{1}{\omega_0 C} \label{resonantfrequency1}
and
\omega_0 = \sqrt{\dfrac{1}{LC}}.\label{resonantfrequency2}
This is the resonant angular frequency of the circuit. Substituting \omega_0 into Equation 15.4.5, Equation 15.4.7, and Equation 15.4.8, we find that at resonance,
\phi = tan^{-1}(0) = 0, \, I_0 = V_0/R, \, and \, Z = R. \nonumber
Therefore, at resonance, an RLC circuit is purely resistive, with the applied emf and current in phase.
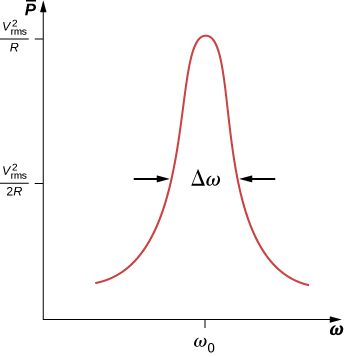
What happens to the power at resonance? Equation 15.5.18 tells us how the average power transferred from an ac generator to the RLC combination varies with frequency. In addition, P_{ave} reaches a maximum when Z, which depends on the frequency, is a minimum, that is, when X_L = X_C and Z = R. Thus, at resonance, the average power output of the source in an RLC series circuit is a maximum. From Equation 15.5.18, this maximum is V_{rms}^2 /R.
Figure \PageIndex{2} is a typical plot of P_{ave} versus \omega in the region of maximum power output. The bandwidth \Delta \omega of the resonance peak is defined as the range of angular frequencies \omega over which the average power P_{ave} is greater than one-half the maximum value of P_{ave}. The sharpness of the peak is described by a dimensionless quantity known as the quality factor Q of the circuit. By definition,
Q = \dfrac{\omega_0}{\Delta \omega}, \label{15.18}
where \omega_0 is the resonant angular frequency. A high Q indicates a sharp resonance peak. We can give Q in terms of the circuit parameters as
Q = \dfrac{\omega_0L}{R}. \label{15.19}
Resonant circuits are commonly used to pass or reject selected frequency ranges. This is done by adjusting the value of one of the elements and hence “tuning” the circuit to a particular resonant frequency. For example, in radios, the receiver is tuned to the desired station by adjusting the resonant frequency of its circuitry to match the frequency of the station. If the tuning circuit has a high Q, it will have a small bandwidth, so signals from other stations at frequencies even slightly different from the resonant frequency encounter a high impedance and are not passed by the circuit. Cell phones work in a similar fashion, communicating with signals of around 1 GHz that are tuned by an inductor-capacitor circuit. One of the most common applications of capacitors is their use in ac-timing circuits, based on attaining a resonant frequency. A metal detector also uses a shift in resonance frequency in detecting metals (Figure \PageIndex{3}).

- What is the resonant frequency of the circuit of Example 15.3.1?
- If the ac generator is set to this frequency without changing the amplitude of the output voltage, what is the amplitude of the current?
Strategy
The resonant frequency for a RLC circuit is calculated from Equation \ref{resonantfrequency2}, which comes from a balance between the reactances of the capacitor and the inductor. Since the circuit is at resonance, the impedance is equal to the resistor. Then, the peak current is calculated by the voltage divided by the resistance.
Solution
- The resonant frequency is found from Equation \ref{resonantfrequency2}: \begin{align*} f_0 &= \dfrac{1}{2\pi} \sqrt{\dfrac{1}{LC}} \\[4pt] &= \dfrac{1}{2\pi}\sqrt{\dfrac{1}{(3.00 \times 10^{-3} H)(8.00 \times 10^{-4}F)}} \\[4pt] &= 1.03 \times 10^2 \, Hz. \end{align*}
- At resonance, the impedance of the circuit is purely resistive, and the current amplitude is I_0 = \dfrac{0.100 \, V}{4.00 \, \Omega} = 2.50 \times 10^{-2}A. \nonumber
Significance
If the circuit were not set to the resonant frequency, we would need the impedance of the entire circuit to calculate the current.
- What is the resonant angular frequency of an RLC circuit with R = 0.200 \, \Omega, \, L = 4.00 \times 10^{-3} H, and C = 2.00 \times 10^{-6}F?
- If an ac source of constant amplitude 4.00 V is set to this frequency, what is the average power transferred to the circuit?
- Determine Q and the bandwidth of this circuit.
Strategy
The resonant angular frequency is calculated from Equation \ref{resonantfrequency2}. The average power is calculated from the rms voltage and the resistance in the circuit. The quality factor is calculated from Equation \ref{15.19} and by knowing the resonant frequency. The bandwidth is calculated from Equation \ref{15.18} and by knowing the quality factor.
Solution
- The resonant angular frequency is \begin{align*} \omega_0 &= \sqrt{\dfrac{1}{LC}} \\[4pt] &= \sqrt{\dfrac{1}{(4.00 \times 10^{-3}H)(2.00 \times 10^{-6}F)}} \\[4pt] &= 1.12 \times 10^4 \, rad/s. \end{align*}
- At this frequency, the average power transferred to the circuit is a maximum. It is P_{ave} = \dfrac{V_{rms}^2}{R} = \dfrac{[(1/\sqrt{2})(4.00 \, V)]^2}{0.200 \, \Omega} = 40.0 \, W. \nonumber
- The quality factor of the circuit is Q = \dfrac{\omega_0L}{R} = \dfrac{(1.12 \times 10^4 \, rad/s)(4.00 \times 10^{-3}H)}{0.200 \, \Omega} = 224. \nonumber We then find for the bandwidth \Delta \omega = \dfrac{\omega_0}{Q} = \dfrac{1.12 \times 10^4 \, rad/s}{224} = 50.0 \, rad/s. \nonumber
Significance
If a narrower bandwidth is desired, a lower resistance or higher inductance would help. However, a lower resistance increases the power transferred to the circuit, which may not be desirable, depending on the maximum power that could possibly be transferred.
In the circuit of Figure 15.4.1, L = 2.0 \times 10^{-3}H, \, C = 5.0 \times 10^{-4} F, and R = 40 \, \Omega.
- What is the resonant frequency?
- What is the impedance of the circuit at resonance?
- If the voltage amplitude is 10 V, what is i(t) at resonance?
- The frequency of the AC generator is now changed to 200 Hz. Calculate the phase difference between the current and the emf of the generator.
- Answer
-
a. 160 Hz; b. 40 \Omega; c. (0.25 A) \, \sin \, 10^3t; d. 0.023 rad
What happens to the resonant frequency of an RLC series circuit when the following quantities are increased by a factor of 4: (a) the capacitance, (b) the self-inductance, and (c) the resistance?
- Answer
-
a. halved; b. halved; c. same
The resonant angular frequency of an RLC series circuit is 4.0 \times 10^2 \, rad/s. An ac source operating at this frequency transfers an average power of 2.0 \times 10^{-2} W to the circuit. The resistance of the circuit is 0.50 \, \Omega. Write an expression for the emf of the source.
- Answer
-
v(t) = (0.14 \, V) \, sin \, (4.0 \times 10^2 t)


