13.12: Quantum Teleportation
( \newcommand{\kernel}{\mathrm{null}\,}\)
INTRODUCTION
In March 1993 Charles H. Bennett from IBM proposed a scheme, based on Quantum Mechanics, that in principle could be used to teleport an object. The scheme was experimentally verified by Dik Bouwmeester et al. in the Fall of 1997. In 2004 researchers at the University of Vienna and the Austrian Academy of Science used an 800m-long optical fibre fed through a public sewer system tunnel to connect labs on opposite sides of the River Danube to achieve such teleportation..
Here we explore this phenomenon of Quantum Teleportation. We will then extend the discussion to Quantum Information and Quantum Cryptography. The document is based on a discussion with an upper year course in modern Physics without mathematics given at the University of Toronto.
Although the discussion is almost totally non-mathematical, it requires considerable understanding of the Quantum Correlation experiments used in describing Bell's Theorem.
TELEPORTATION
In Star Trek, when Captain Kirk is beamed from the starship Enterprise to the surface of a planet, Captain Kirk de-materialises on the Enterprise, and then re-materialises on the planet. On the TV show, an unanswered question is whether the transporter physically disassembles Captain Kirk, moves the atoms from his body to the planet, and then reassembles them. Another perhaps more reasonable alternative would be to scan all the information about Captain Kirk's physical state, and transmit that information to the planet surface where it is used to construct a new Captain Kirk out of raw materials found on the planet. Note that in either case the transporter needs to have complete information on Kirk's physical state in order to reconstruct him.
However, the Heisenberg Uncertainty Principle means that it is impossible to obtain this complete information about Kirk. Thus, it seems that the best the transporter can do is make an approximate copy of him on the planet surface. Quantum Teleportation provides a way to "beat" the Uncertainty Principle and make an exact copy.
As we shall see, the mechanism that beats the Uncertainty Principle is the same one used to beat it in the Quantum Correlation experiments we examined when we discussed Bell's Theorem. We shall also see that although the collapse of the state for the two measurements in the correlation experiments occurs instantaneously, the teleportation can not occur faster than the speed of light.
Finally, a little terminology. Before we were discussing Quantum Correlation experiments in which we were measuring the spins of two separate electrons whose total spin was zero. We call the states of those two electrons entangled.
BELL-STATE MEASUREMENTS
In previous discussions we almost always talked about the spin state of electrons, although we regularly pointed out that the same situations exist for the polarization of light, albeit with a difference of a factor of 2 in the angles being used. Here we will reverse the situation, and mostly talk about polarization states for photons, although the arguments also apply to spin states of electrons.
The fact that we may talk about light polarization in almost the same way that we discuss electron spin is not a coincidence. It turns out that photons have spins which can exist in only two different states. And those different spins states are related to the polarization of the light when we think of it as a wave.
Here we shall prepare pairs of entangled photons with opposite polarizations; we shall call them E1 and E2. The entanglement means that if we measure a beam of, say, E1 photons with a polarizer, one-half of the incident photons will pass the filter, regardless of the orientation of the polarizer. Whether a particular photon will pass the filter is random. However, if we measure its companion E2 photon with a polarizer oriented at 90 degrees relative to the first, then if E1 passes its filter E2 will also pass its filter. Similarly if E1 does not pass its filter its companion E2 will not.
Earlier we discussed the Michelson-Morley experiment, and later the Mach-Zehnder interferometer. You will recall that for both of these we had half-silvered mirrors, which reflect one-half of the light incident on them and transmit the other half without reflection. These mirrors are sometimes called beam splitters because they split a light beam into two equal parts.
We shall use a half-silvered mirror to perform Bell State Measurements. The name is after the originator of Bell's Theorem.
|
We direct one of the entangled photons, say E1, to the beam splitter. Meanwhile, we prepare another photon with a polarization of 450, and direct it to the same beam splitter from the other side, as shown. This is the photon whose properties will be transported; we label it K (for Kirk). We time it so that both E1 and K reach the beam splitter at the same time. |
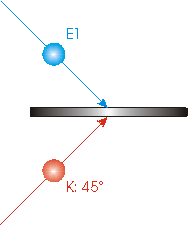 |
|
The E1 photon incident from above will be reflected by the beam splitter some of the time and will be transmitted some of the time. Similarly for the K photon that is incident from below. So sometimes both photons will end up going up and to the right as shown. Similarly, sometimes both photons will end up going down and to the right. |
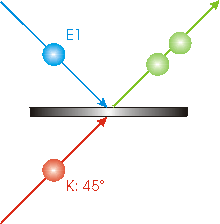 |
|
But sometimes one photon will end up going upwards and the other will be going downwards, as shown. This will occur when either both photons have been reflected or both photons have been transmitted. Thus there are three possible arrangements for the photons from the beam splitter: both upwards, both downwards, or one upwards and one downwards. Which of these three possibilities has occurred can be determined if we put detectors in the paths of the photons after they have left the beam splitter. However, in the case of one photon going upwards and the other going downwards, we can not tell which is which. Perhaps both photons were reflected by the beam splitter, but perhaps both were transmitted. This means that the two photons have become entangled. If we have a large beam of identically prepared photon pairs incident on the beam splitter, the case of one photon ending up going upwards and the other downwards occurs, perhaps surprisingly, 25% of the time. |
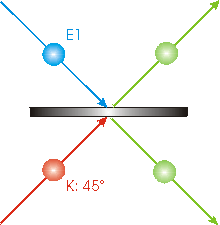 |
Also somewhat surprisingly, for a single pair of photons incident on the beam splitter, the photon E1 has now collapsed into a state where its polarization is -450, the opposite polarization of the prepared 450 one. This is because the photons have become entangled. So although we don't know which photon is which, we know the polarizations of both of them.
The explanation of these two somewhat surprising results is beyond the level of this discussion, but can be explained by the phase shifts the light experiences when reflected, the mixture of polarization states of E1, and the consequent interference between the two photons.
THE TELEPORTER
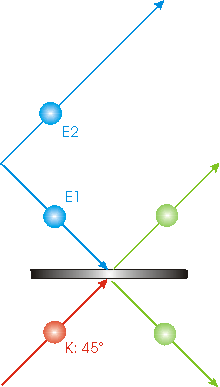 Now we shall think about the E2 companion to E1.
Now we shall think about the E2 companion to E1.
25 percent of the time, the Bell-state measurement resulted in the circumstance shown, and in these cases we have collapsed the state of the E1 photon into a state where its polarization is -450.
But since the two photon system E1 and E2 was prepared with opposite polarizations, this means that the companion to E1, E2, now has a polarization of +450. Thus the state of the K photon has now been transferred to the E2 photon. We have teleported the information about the K photon to E2.
Although this collapse of E2 into a 450 polarization state occurs instantaneously, we haven't achieved teleportation until we communicate that the Bell-state measurement has yielded the result shown. Thus the teleportation does not occur instantaneously.
Note that the teleportation has destroyed the state of the original K photon.
Quantum entanglements such as exist between E1 and E2 in principle are independent of how far apart the two photons become. This has been experimentally verified for distances as large as 10km. Thus, the Quantum Teleportation is similarly independent of the distance.
The Original State of the Teleported Photon Must Be Destroyed
Above we saw that the K photon's state was destroyed when the E2 photon acquired it. Consider for a moment that this was not the case, so we end up with two photons with identical polarization states. Then we could measure the polarization of one of the photons at, say, 450 and the other photon at 22.50. Then we would know the polarization state of both photons for both of those angles.
As we saw in our discussion of Bell's Theorem, the Heisenberg Uncertainty Principle says that this is impossible: we can never know the polarization of a photon for these two angles. Thus any teleporter must destroy the state of the object being teleported.
OTHER APPLICATIONS
Teleporting the polarization state of a single photon a quarter of the time is a long long way from reliably teleporting Captain Kirk. However, there are other applications of the above sort of apparatus that may be closer to being useful.
Quantum Information
As you probably know, computers store information as sequences of 0's and 1's. For example, in the ASCII encoding the letter A is represented by the number 65. As a binary number this is:
1,000,001
Inside the computer, there are transistors that are either on or off, and we assign the on-state be 1 and the off state 0. However, the same information can be stored in exactly the same way in any system that has two mutually exclusive binary states.
For example, if we have a collection photons we could represent the 1's as photons whose polarization is +450 and the 0's as polarizations of -450. We could similarly use electrons with spin-up and spin-down states to encode the information. These quantum bits of information are called qubits.
Above we were thinking about an apparatus to do Quantum Teleportation. Now we see that we can think of the same apparatus as transferring Quantum Information. Note that, as opposed to, say, a fax, when transferring Quantum Information the original, the polarization of the K photon, is destroyed.
Quantum Cryptography
Cryptography depends on both the sender and receiver of the encrypted information both knowing a key. The sender uses the key to encrypt the information and the receiver uses the same key to decrypt it.
The key can be something very simple, such as both parties knowing that each letter has been shifted up by 13 places, with letters above the thirteenth in the alphabet rotated to the beginning. Or they can be very complex, such as a very very long string of binary digits.
Here is an example of using binary numbers to encrypt and decrypt a message, in this case the letter A, which we have seen is 1,000,001 in a binary ASCII encoding. We shall use as the key the number 23, which in binary is 0,010,111. We will use the key to encode the letter using a rule that if the corresponding bits of the letter and key are the same, the result is a 1, and otherwise a 0.
| A | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|---|
| Key | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| Encrypted | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
The encrypted value is 41, which in ASCII is the right parenthesis: )
To decrypt the message we use the key and the same procedure:
| Encrypted | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|---|
| Key | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| A | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Any classical encryption scheme is vulnerable on two counts:
- If the "bad guys" get hold of the key they too can decrypt the message. So-called public key encryptation schemes reveals on an open channel a long string of binary digits which must be converted to the key by means of a secret procedure; here security is based on the computational complexity of "cracking" the secret procedure.
- Because there are patterns in all messages, such as the fact that the letter e predominates, then if multiple messages are intercepted using the same key the bad guys can begin to decipher them.
To be really secure, then, there must be a unique secret key for each message. So the question becomes how can we generate a unique key and be sure that the bad guys don't know what it is.
To send a key in Quantum Cryptography, simply send photons in one of four polarizations: -45, 0, 45, or 90 degrees. As you know, the receiver can measure, say, whether or not a photon is polarized at 90 degrees and if it is not then be sure than it was polarized at 0 degrees. Similarly the receiver can measure whether a photon was polarized at 45 degrees, and if it is not then it is surely polarized at -45 degrees. However the receiver can not measure both the 0 degree state and 45 degree state, since the first measurement destroys the information of the second one, regardless of which one is performed first.
The receiver measures the incoming photons, randomly choosing whether to measure at 90 degrees or 45 degrees, and records the results but keeps them secret. The receiver contacts the sender and tells her on an open channel which type of measurement was done for each, without revealing the result. The sender tells the receiver which of the measurements were of the correct type. Both the sender and receiver keep only the qubits that were measured correctly, and they have now formed the key.
If the bad guys intercept the transmission of photons, measure their polarizations, and then send them on to the receiver, they will inevitably introduce errors because they don't know which polarization measurement to perform. The two legitimate users of the quantum channel test for eavesdropping by revealing a random subset of the key bits and checking the error rate on an open channel. Although they cannot prevent eavesdropping, they will never be fooled by an eavesdropper because any, however subtle and sophisticated, effort to tap the channel will be detected. Whenever they are not happy with the security of the channel they can try to set up the key distribution again.
By February 2000 a working Quantum Cryptography system using the above scheme achieved the admittedly modest rates of 10 bits per second over a 30 cm length.
There is another method of Quantum Cryptography which uses entangled photons. A sequence of correlated particle pairs is generated, with one member of each pair being detected by each party (for example, a pair of photons whose polarisations are measured by the parties). An eavesdropper on this communication would have to detect a particle to read the signal, and retransmit it in order for his presence to remain unknown. However, the act of detection of one particle of a pair destroys its quantum correlation with the other, and the two parties can easily verify whether this has been done, without revealing the results of their own measurements, by communication over an open channel.
Author
David M. Harrison, Department of Physics, University of Toronto, harrison@physics.utoronto.ca.

