Sample Problems

All of the problems below have had their basic features discussed in an "Analyze This" box in this chapter. This means that the solutions provided here are incomplete, as they will refer back to the analysis performed for information (i.e. the full solution is essentially split between the analysis earlier and details here). If you have not yet spent time working on (not simply reading!) the analysis of these situations, these sample problems will be of little benefit to your studies.

Problem 3.1

A toy train rolls along a straight, frictionless track, parallel to the \(x\)-axis.  As it rolls, it experiences a force given by the equation:

\[\vec F = F\left(x\right)\left[0.600\;\hat i + 0.800\;\hat j\right]\nonumber\]

The function \(F\left(x\right)\) can be expressed by the graph below.

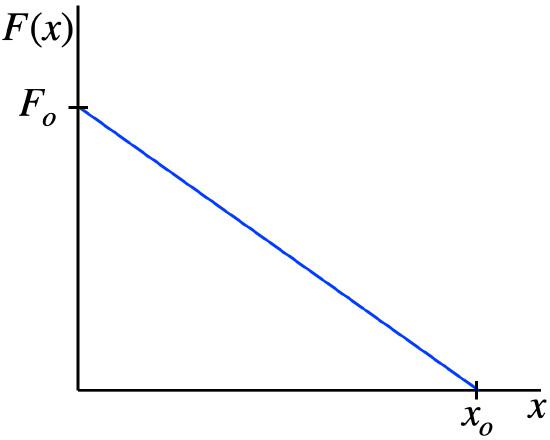
The train starts at the position \(x_o=12m\) with a speed of \(3.0\frac{m}{s}\), moving in the \(-x\) direction, and the force stops it when it gets halfway to the origin. If the same train is then picked up and placed on the track at the origin, find its acceleration.

Solution

As we saw in the analysis, the work done by this force on the train when it moves along the \(x\)-axis is 0.60 times the area under the graph given.  In this case, the displacement of the train is from \(x_o\) to \(\frac{1}{2}x_o\), so we use the area for that interval to compute the work (and since the displacement is in the \(-x\)-direction, this work is negative).  The maximum force reached is \(\frac{1}{2}F_o\), so area of this triangle is:

\[\text{area under curve} = \frac{1}{2}bh = \frac{1}{2}\left(\frac{1}{2}x_o\right)\left(\frac{1}{2}F_o\right)= \frac{1}{8}F_ox_o\nonumber\]

The work done by the force during the train's journey is therefore:

\[W=-0.600\left(\text{area under graph}\right)=-0.60\left(\frac{1}{8}F_ox_o\right) = -F_o\left(0.90m\right) \nonumber\]

This work results in a change of the train's kinetic energy, according to the work-energy theorem.  The final kinetic energy is zero (the train stops), so:

\[W=\Delta KE = \frac{1}{2}mv_f^2-\frac{1}{2}mv_o^2-\;\;\;\Rightarrow\;\;\; -F_o\left(0.9m\right) = 0-\frac{1}{2}m\left(3.0\frac{m}{s}\right)^2\;\;\;\Rightarrow\;\;\; F_o=m_o\left(5.0\frac{m}{s^2}\right)\nonumber\]

If the train is now placed at the origin, then the net force by the train + tracks will be in the \(+x\) direction (the tracks exert a force on the train that won't let it move any other way), so only the \(x\)-component of the force will contribute to the acceleration. The train therefore feels a net force of \(0.60F_o\), and dividing this by the mass of the train gives its acceleration, according to Newton's 2nd Law. The equation above gives us this ratio:

\[a = \frac{0.60F_o}{m} = 3.0\frac{m}{s^2}\nonumber\]

Problem 3.2

Three identical particles, A, B, and C are positioned at the vertices of an equilateral triangle. Particle A remains at rest at the origin, while particles B and C move directly away from particle A at equal speeds along the lines defined by the triangle, as shown in the diagram.

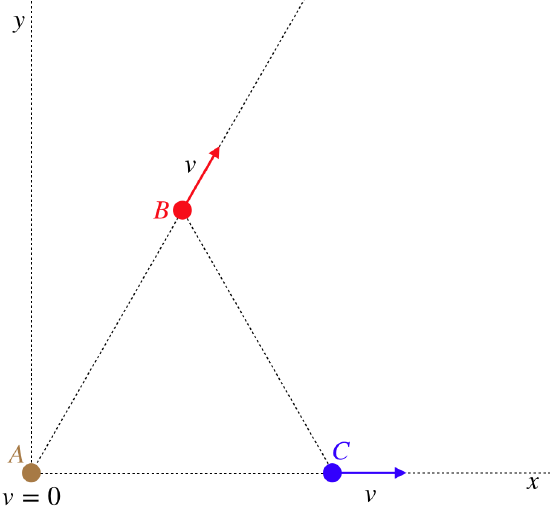
The kinetic energy of each particle is \(10J\).

1. Find the internal energy of the three-particle system.
2. Find the internal energy of the two-particle system \(AB\).
3. Find the internal energy of the two-particle system \(BC\).

Solution

a. We anticipated this question in the analysis, so we will not reproduce the work here.  There we found that the internal energy of the three-particle system was \(\frac{1}{2}mv^2\), which is the same as the kinetic energy of a single particle (measured in the diagramed frame of reference), which here is 10J.

b. The internal energy is found by subtracting the system's collective kinetic energy from its total energy, the latter of which can be found using the kinetic energies of the individual particles. Clearly, therefore, the total energy of the \(AB\) system in the reference frame given is \(10J\). The system's collective kinetic energy comes from the motion of its center of mass. With just two particles of equal mass involved, the center of mass speed is:

\[v_{cm}=\frac{m_1v_1+m_2v_2}{m_1+m_2}=\frac{mv+0}{m+m}=\frac{1}{2}v\nonumber\]

The kinetic energy of the \(AB\) system is therefore:

\[{KE}_{system\;AB}=\frac{1}{2}Mv_{cm}^2=\frac{1}{2}\left(2m\right)\left(\frac{1}{2}v^2\right)=\frac{1}{2}\left(\frac{1}{2}mv^2\right)=\frac{1}{2}{KE}_B=5J\nonumber\]

Subtracting this from the total energy of the two-particle system gives us its internal energy:

\[E_{int\;AB}=E_{tot\;AB}-{KE}_{system\;AB}=\left({KE}_A+{KE}_B\right)-KE_{system\;AB}=\left(0+10J\right)-5J=5J\nonumber\]

c. If we think about what the arrangement of particles looks like at later times, we conclude that it remains an equilateral triangle, but just a bigger one. This means that if we looked at the motion of \(C\) from the perspective of \(B\), we would see exactly the same thing as viewing \(B\)'s motion from \(A\)'s perspective. The internal energy is independent of the frame from which we view it, so the internal energy of the \(BC\) system must be the same as it is for the \(AB\) system. We can of course confirm this with lots of velocity vector math. Sigh, okay, here it is... Place \(A\) at the origin, and \(C\) moves along the -axis, while \(B\) moves away from the origin in a direction 60º above the -axis. The velocity vectors are therefore:

\[\vec v_B = v\left(\cos 60^o\hat i + \sin 60^o\hat j\right) = \frac{1}{2}v\left(\hat i + \sqrt 3 \hat j\right)\; ,\;\;\;\;\;\vec v_C=v\hat i\nonumber\]

The center of mass velocity of the system \(BC\) is:

\[\vec v_{cm}=\frac{m\vec v_B+m\vec v_C}{m+m}=\frac{1}{4}v\left(3\hat i + \sqrt{3} \hat j\right)\nonumber\]

This makes the system's collective kinetic energy equal to:

\[KE_{system\;BC} = \frac{1}{2}Mv_{cm}^2 = \frac{1}{2}\left(2m\right)\left(\frac{1}{4}v\right)^2\left(3^3+\sqrt{3}^2\right)=\frac{3}{4}mv^2\nonumber\]

The system's total energy is the sum of the kinetic energies of the two particles \(B\) and \(C\), which is just \(E_{tot;BC}=mv^2\). So the internal energy is:

\[E_{int\;BC}=E_{tot\;BC}-{KE}_{system\;AB}=mv^2-\frac{3}{4}mv^2=5J\nonumber\]

This confirms that it is the same internal energy as the system \(AB\).

Problem 3.3

Consider the following forces that act on a particle as it moves in the \(\left(x,y\right)\) plane (\(\alpha\) is a constant):

• \(\overrightarrow F\left(x,y\right)=\alpha\left(x \;\hat i-y \;\hat j\right)\)
• \(\overrightarrow F\left(x,y\right)=\alpha\left(y \;\hat i-x \;\hat j\right)\)

Check each of these forces to determine if it is conservative, in each of the following ways:

1. Use the partial derivative check (Equation 3.3.8).
2. Compute the work done by each force on a particle that moves from the origin to the point \(\left(2,4\right)\) in the \(\left(x,y\right)\) plane over the following two paths:

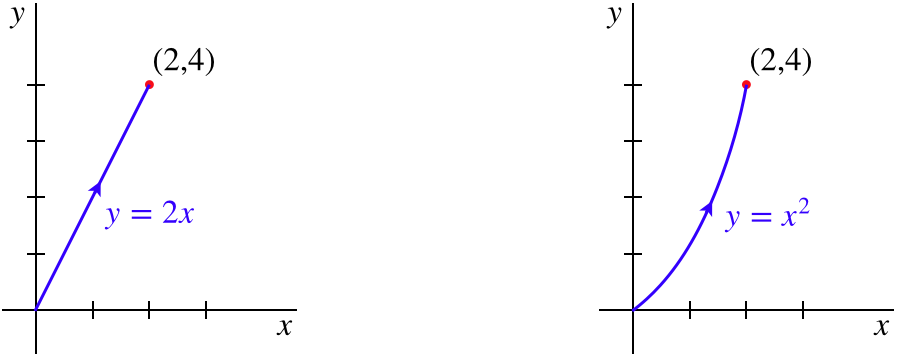
Solution

a. We already did this in the analysis.

b. This method is quite a bit tougher (which makes us thankful for the partial derivative method). You may want to review the discussion of line integrals for more guidance on how this works. We have two line integrals to perform for each force – one following the linear path and one following the parabolic path.  In every case, the infinitesimal displacement vector can be written as:

\[\overrightarrow{dl} = dx\;\hat i + dy\;\hat j = \left(\hat i + \frac{dy}{dx}\hat j\right)dx\nonumber\]

Evaluating this vector on the specific path being used is then just a simple matter of knowing the derivative for that path, and the integral can then be performed over \(x\) between the endpoints of the path (for both of these paths, that will be \(x:0\rightarrow 2\)). The thing to always keep in mind is that anything we evaluate must be specific to the path, and we are converting everything to the single variable \(x\) so we can perform the integral.  This will become clear below.

\(\overrightarrow F\left(x,y\right)=\alpha\left(x\;\hat i-y\;\hat j\right)\) 

\[W=\int \limits_{lin} \vec F\cdot \overrightarrow{dl} = \int \limits_{x=0}^{x=2}\alpha\left(x\;\hat i-y\;\hat j\right)\cdot \left(\hat i + \frac{dy}{dx}\hat j\right)dx=\alpha\int \limits_{x=0}^{x=2}\left(x-y\frac{dy}{dx}\right)dx\nonumber\]

Linear path, so \(y=2x\) and \(\frac{dy}{dx}=2\):

\[W=\alpha\int \limits_{x=0}^{x=2} \left[x - \left(2x\right)\left(2\right)\right]dx=\left[-\frac{3}{2}\alpha x^2\right]_0^2=-6\alpha\nonumber\]

Parabolic path, so \(y=x^2\) and \(\frac{dy}{dx}=2x\):

\[W=\alpha\int \limits_{x=0}^{x=2} \left[x - \left(x^2\right)\left(2x\right)\right]dx=\alpha\left[\frac{1}{2} x^2-\frac{1}{2}x^4\right]_0^2=-6\alpha\nonumber\]

The two line integrals along different paths between the same endpoints yield the same answer, as they should for this force that we have already determined to be conservative. Now for the second force:

\(\overrightarrow F\left(x,y\right)=\alpha\left(y\;\hat i-x\;\hat j\right)\) 

\[W=\int \limits_{lin} \vec F\cdot \overrightarrow{dl} = \int \limits_{x=0}^{x=2}\alpha\left(y\;\hat i-x\;\hat j\right)\cdot \left(\hat i + \frac{dy}{dx}\hat j\right)dx=\alpha\int \limits_{x=0}^{x=2}\left(y-x\frac{dy}{dx}\right)dx\nonumber\]

Linear path, so \(y=2x\) and \(\frac{dy}{dx}=2\):

\[W=\alpha\int \limits_{x=0}^{x=2} \left[2x - \left(x\right)\left(2\right)\right]dx=0\nonumber\]

Parabolic path, so \(y=x^2\) and \(\frac{dy}{dx}=2x\):

\[W=\alpha\int \limits_{x=0}^{x=2} \left[x^2 - \left(x\right)\left(2x\right)\right]dx=\alpha\left[-\frac{1}{3} x^3\right]_0^2=-\frac{8}{3}\alpha\nonumber\]

These two line integrals are not equal, which confirms that this force in non-conservative.

Problem 3.4

A small block slides along a frictionless, horizontal surface into a frictionless vertical half-circle track, and it remains in contact with the track, until at least the \(\theta=90^o\) point (with \(\theta\) defined in the diagram).

Find the fraction of kinetic energy lost by the block in getting to the top of the half-circle, if it just barely maintains contact with the track at the top.

Solution

In the analysis, we found a relationship between the block's initial and final speeds, in terms of the angle \(\theta\). In this case, we are interested in its speed at the top, so \(\theta = 180^o\), giving:

\[v_f^2=v_o^2-2gR\left(1-\cos 180^o\right) = v_o^2-4gR\nonumber\]

We also found in the analysis an expression for the minimum velocity needed for the block to remain in contact with the track, as a function of the angle \(\theta\). As we are given that the block barely remains in contact at the top of the half-circle, we must assume that it has the minimum speed it can have at this point. This speed is the "final" speed, so we have:

\[v_f^2 = -gR\cos 180^o=gR\nonumber\]

So we have \(v_f^2\) in terms of \(R\), and combining these two equations allows us to do the same for \(v_o^2\):

\[gR = v_o^2-4gR\;\;\;\Rightarrow\;\;\; v_o^2=5gR\nonumber\]

Now all we have to do is construct the kinetic energy ratio requested:

\[\frac{KE_{lost}}{KE_o} = \frac{KE_o-KE_f}{KE_o} = \frac{\frac{1}{2}mv_o^2-\frac{1}{2}mv_f^2}{\frac{1}{2}mv_o^2}=\frac{v_o^2-v_f^2}{v_o^2}=\frac{5gR-gR}{5gR}=0.8\nonumber\]

Problem 3.5

A block is attached to a vertical spring, the other end of which is attached to the ceiling. The block is held stationary at a height where the spring is at its equilibrium length. The block is then released.

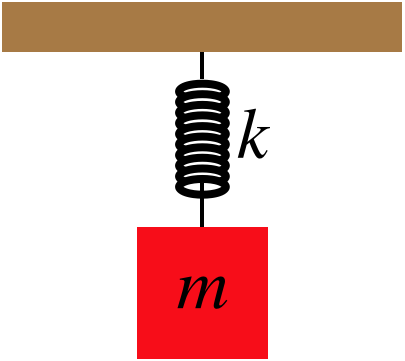
The block falls a distance of \(120cm\) before finally stopping and bouncing back up. Find the distance it has fallen when it reaches its maximum speed.

Solution

With some thought, the analysis actually gives us the answer immediately. We found that the position where the spring force cancels the gravity force is exactly halfway between the top and the bottom, which we also found to be the position where the spring and gravity forces are equal. The gravity force is unchanging, so slightly above this midway position, the spring stretch is not quite enough to produce a force as great as the force of gravity. This means that everywhere above this midway point there is a net force downward.  So the block continues speeding up in its descent until it reaches the midway point. After crossing the midway point, the spring force is greater than the gravity force, so the block slows down.  Therefore the block reaches a maximum speed after dropping \(60cm\).

Okay, now let's do it the "cool" mathematical way, using the work-energy theorem. If we call the starting point of the block \(y=0\) and treat downward as the \(+y\)-direction, then from the equation we found in the analysis, we have the total work done on the block in terms of \(y\), and we can set it equal to the kinetic energy at the position \(y\) (yes, the work done equals the change in kinetic energy, but the block starts from rest, so the change equals the kinetic energy itself):

\[KE\left(y\right)=W\left(0\rightarrow y\right)=-\frac{1}{2}ky^2+mgy\nonumber\]

We want to know the value of \(y\) where the speed of the block is a maximum.  Well, obviously this occurs where the kinetic energy is a maximum (the block's mass doesn't change). So maximizing the \(KE\left(y\right)\) function gives:

\[0=\frac{d}{dy}KE\left(y\right)=-ky+mg\;\;\;\Rightarrow\;\;\; y=\frac{mg}{k}\nonumber\]

We already found in the analysis that the maximum stretch of the spring is twice this value, so once again we find that the \(y\) value where the block is moving fastest is \(60cm\).

Problem 3.6

A puck is slid along a horizontal rough surface in a straight line along the diameter of a circle (the gravity, contact and friction forces are the only forces on the puck).  The same puck is then slid on the same surface starting at the same speed along the circle defined by the diameter indicated in the first experiment (it slides around the inside surface of a frictionless circular wall). The figure shown depicts a top view of these two paths.

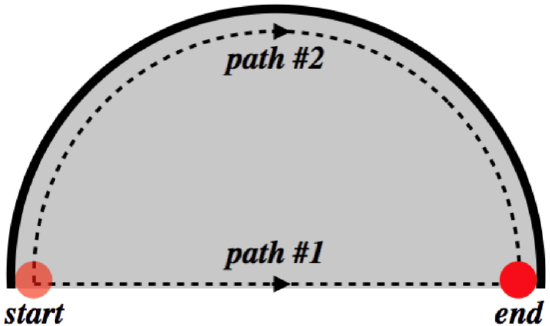
The puck is pushed at the start point so that it slides around path #2, and it just comes to rest at the end point. If it is pushed at the same speed from the start point along path #1, find the fraction of initial speed that it has lost when it reaches the end point.

Solution

In the analysis we found that the work done by friction over path #2 is greater than the work done by friction over path #1 by a factor of \(\frac{\pi}{2}\). From the work-energy theorem, this means that the changes in kinetic energy for these two paths are related in the same way:

\[\Delta{KE}_2=\frac{\pi}{2}\Delta{KE}_1\;\;\;\Rightarrow\;\;\;0-\frac{1}{2}mv^2_o=\frac{\pi}{2}\left(\frac{1}{2}mv^2_f-\frac{1}{2}mv^2_o\right)\nonumber\]

Solving for the final velocity in terms of the initial velocity gives:

\[v_f=\sqrt{1-\frac{2}{\pi}}\;v_o=0.60v_o\nonumber\]

So the puck loses about 40% of its speed along path #1.

Problem 3.7

There are few things as fun as swinging into a river from a rope swing tied to the limb of a tree on its banks. The person at the end of this rope starts at the top of a hill at one angle, then swings to another angle when they let go and fly into the water.

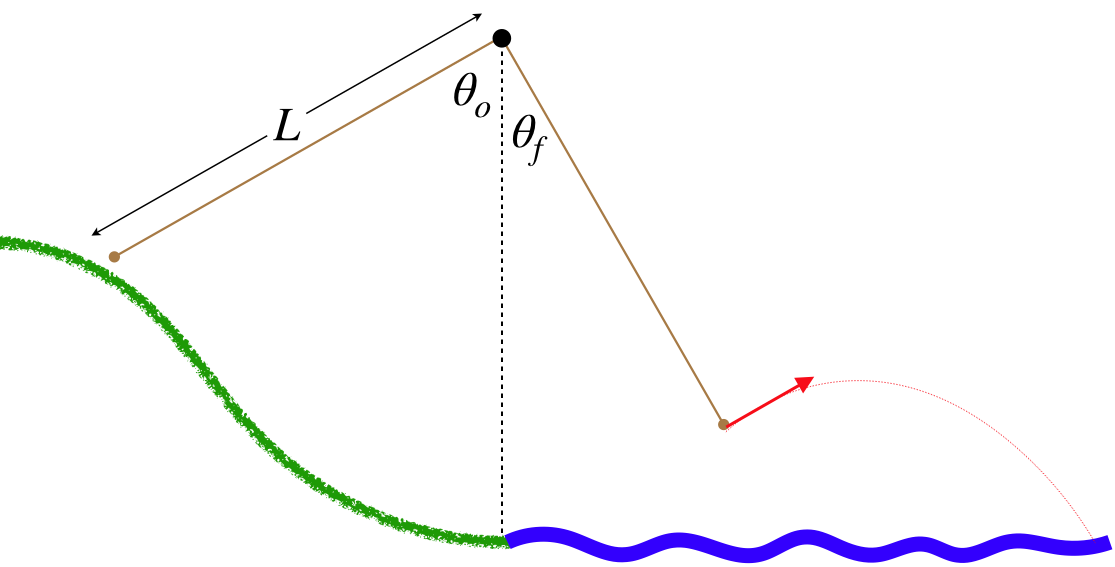
The length of the rope is \(6.0m\), and the starting and ending angles are \(\theta_o=60^o\) and \(\theta=30^o\), respectively. The end of the rope when it hangs vertically at the shoreline is \(2.4m\) above the water level. You start from rest (don't get a running start).

1. Find your speed at the point when you release the rope.
2. Find the distance above the water that you reach at the peak of your flight.

Solution

a. We solved this in the analysis, so all that remains is to plug in the numbers. The initial speed is zero, and the length of the rope and angles are given, so:

\[v_f=\sqrt{v_o^2 - gL \left( \cos \theta_o-\cos \theta_f \right)}=\sqrt{0 - \left(9.8\frac{m}{s^2}\right)\left(6.0m\right) \left(\cos 60^o-\cos 30^o \right)}=6.6\frac{m}{s}\nonumber\]

b. We know that at the point of release, the velocity vector makes a 30º angle with the horizontal, so the horizontal component of this velocity (which never changes) is:

\[ v_x = v \cos 30^o = 5.6 \frac{m}{s} \nonumber \]

When you hit your peak height, you will have a zero \(y\)-component of velocity, so the quantity above will be your total speed. Given we are ignoring air resistance, the only work is being done throughout is by gravity, which means we can use the same method as in the analysis – whether the rope is involved throughout or not is irrelevant. So again calling the height of the tree limb \(y=0\), we have:

\[-\Delta KE=\Delta U_{grav} = mg \left(y_f - y_o \right) = mgy_f-mg\left(-L\cos 30^o\right)\;\;\;\Rightarrow\;\;\;y_f=\frac{1}{2g}v_f^2-L\cos 30^o\nonumber\]

Plugging in for \(L\), and \(v_x\) for \(v_f\), we get:

\[y_f = \frac{\left(5.6\frac{m}{s}\right)^2}{2\left(9.8\frac{m}{s^2}\right)}-\left(6.0m\right)\cos 30^o=-3.6m\nonumber\]

This is the distance below the tree branch, and since we know how high the tree branch is above the water, we have our answer:

\[h=6.0m+2.4m-3.6m=4.8m\nonumber\]

Problem 3.8

A bead is threaded onto a frictionless circular loop that lies in the horizontal \(x\)-\(y\) plane, as shown in the diagram below. This bead is subjected to a conservative force that is characterized by the potential energy function:

\[U\left(x,y\right)=-\alpha\left(Rx+y^2\right)\;\;\;\;\;\alpha > 0\nonumber\]

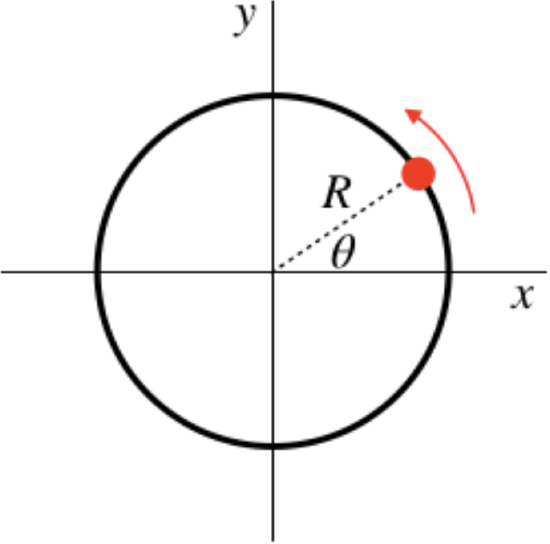
The physical values for this set up are as follows: \(\alpha = 0.05\frac{kg}{s^2}\),  \(R = 16cm\),  mass of bead \(=4.0g\). The bead travels counterclockwise around the loop, and makes it all the way around the circle without stopping, with its minimum speed measured to be: \(90\frac{cm}{s}\). Find the maximum speed attained by the bead.

Solution

We determined in the analysis the maximum and minimum potential energies, and these correspond to the minimum and maximum kinetic energies, respectively. We are also given the minimum speed of the bead, so if we apply the conservation of energy to the change that occurs between the maxes and mins, we get:

\[0=\Delta KE + \Delta U\;\;\;\Rightarrow\;\;\;{KE}_{max}={KE}_{min}+U_{max}-U_{min}\nonumber\]

Putting in the expressions for the kinetic energies and the results from the analysis for the potential energies, we get:

\[\frac{1}{2}mv_{max}^2 = \frac{1}{2}mv_{min}^2 +\left(+\alpha R^2\right)-\left(-\frac{5}{4}\alpha R^2\right)\;\;\;\Rightarrow\;\;\;v_{max}=\sqrt{v_{min}^2+\frac{9\alpha R^2}{2m}}\nonumber\]

And finally, plugging in the values gives:

\[v_{max}=\sqrt{\left(0.9\frac{m}{s}\right)^2+\frac{9\left(0.05\frac{kg}{s^2}\right) \left(0.16m\right)^2}{2\left(0.004kg\right)}}=1.5\frac{m}{s}\nonumber\]

Problem 3.9

A ball is launched straight up into the air with the apparatus shown below. The ball is pushed upward so that it compresses the spring, and is released from rest. It then travels around a frictionless half-circle track, at the bottom of which is a scale that measures the contact force the ball exerts on the track at that point.

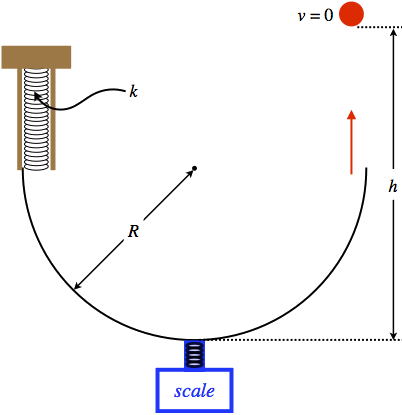
The mass of the ball is \(m=0.400kg\), the stiffness of the spring is \(k=22.0\frac{N}{m}\), the radius of the track is \(R=1.60m\), and at the moment the ball is above the scale, the scale reads \(F_{scale}=18.5N\).

1. Find the speed of the ball as it passes the scale.
2. Find the height \(h\) reached by the ball when it comes to rest.
3. Find the amount that the spring was compressed before the ball was released.

Solution

a. In the analysis, we found the relationship between the speed of the ball and the scale reading. We now know the ball's mass and the radius of the track, so:

\[ F_{scale} - mg = ma_c = m \dfrac{v^2}{R} \;\;\; \Rightarrow \;\;\; v = \sqrt{R \left( \frac{N}{m} - g \right)} = \sqrt{\left(1.60m\right) \left( \frac{18.5N}{0.400kg} - 9.8\frac{m}{s^2} \right)} =7.64 \frac{m}{s} \nonumber \]

b. There is no friction force by the track, and the contact force it exerts is perpendicular to the motion, so it does no work, which means that mechanical energy is conserved. With the speed of the ball at the bottom, we can therefore compute the height it reaches, where it comes to rest:

\[0 = \Delta KE + \Delta U_{grav} = \frac{1}{2} mv_f^2 - \frac{1}{2} mv_o^2 + mgh \;\;\; \Rightarrow \;\;\; h = \dfrac{v_o^2}{2g} =\dfrac{\left(7.64 \frac{m}{s}\right)^2}{2\left(9.8\frac{m}{s^2}\right)}= 2.98m \nonumber \]

c. We know the total energy in the system, either from the KE at the scale, or the PE at the peak height:

\[ E_{tot} = mgh =\left(0.400kg\right)\left(9.8\frac{m}{s^2}\right)\left(2.98m\right) = 11.7J \nonumber \]

When the ball compressed the spring, it had no KE, so all of this energy was stored in the PE of gravity and the elastic PE of the spring. Calling the compression \(\Delta y\), then the height of the ball at the start is \(R+\Delta y\). Summing the two PE’s and setting the sum equal to the total energy gives a quadratic equation, which we then solve for \(\Delta y\):

\[ E_{tot} = mg \left(R+\Delta y \right) +\frac{1}{2}k\left(\Delta y\right)^2\;\;\;\Rightarrow\;\;\;\Delta y =\dfrac{-mg \pm \sqrt{\left(mg\right)^2 - 2k\left(mgR-E_{tot}\right)}}{k}\nonumber\]

\[\Delta y = \dfrac{-\left(0.400kg\right)\left(9.8\frac{m}{s^2}\right) \pm \sqrt{\left(0.400kg\right)^2\left(9.8\frac{m}{s^2}\right)^2 - 2\left(22.0\frac{N}{m}\right)\left(\left(0.400kg\right)\left(9.8\frac{m}{s^2}\right)\left(1.60m\right)-11.7J\right)}}{22.0\frac{N}{m}} = 0.55m \nonumber \]

Problem 3.10

A puck slides down a frictionless track, over a short horizontal rough (frictional) patch, around a frictionless loop-de-loop, and into an ideal spring fixed to a wall, where it bounces off and goes back the other way, returning through the loop-de-loop, over the rough patch, and back up the ramp.

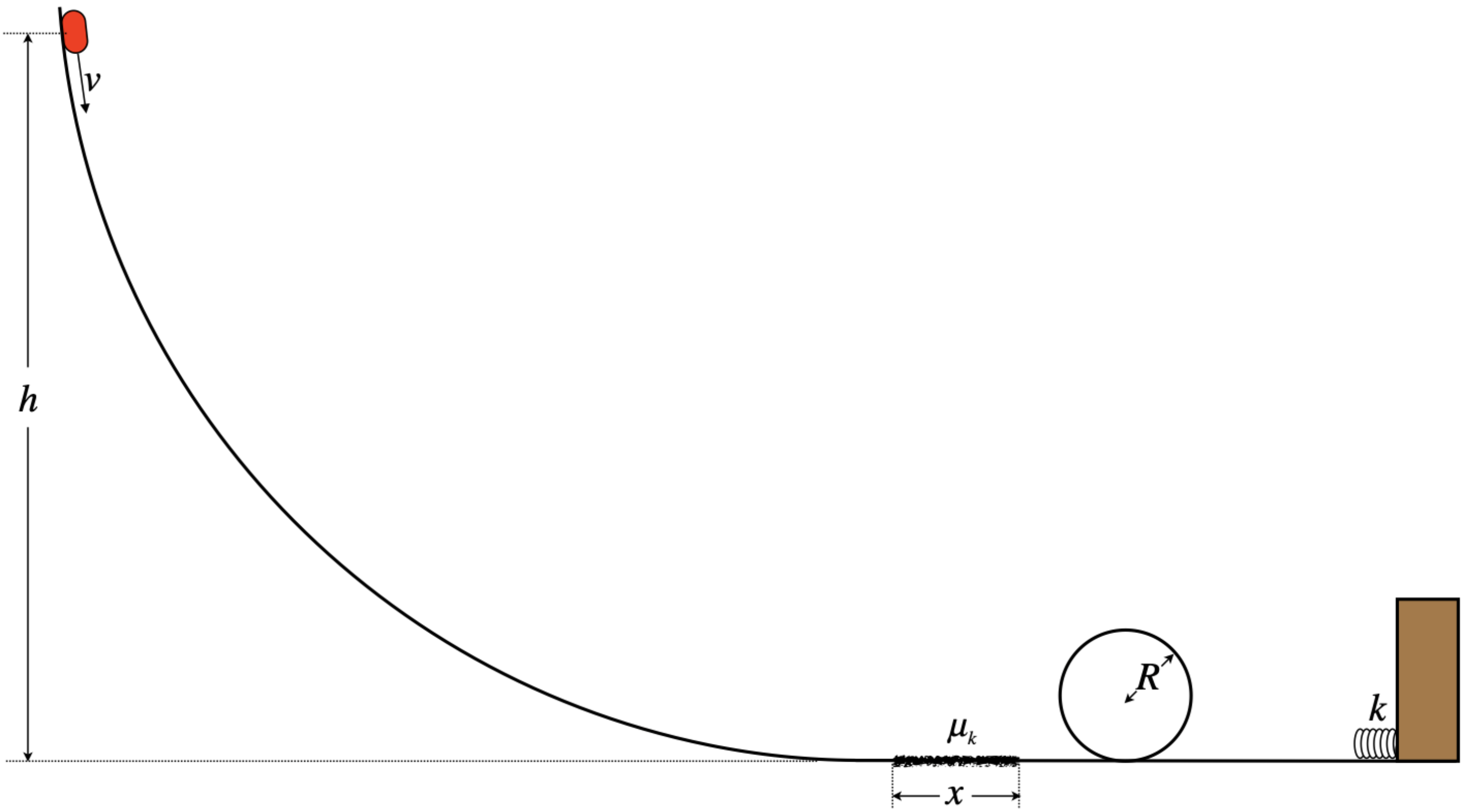
The coefficient of kinetic friction for the rough patch is \(0.30\), and the length of that patch is \(0.80cm\). The puck bounces off the spring one time, and eventually comes to rest, without ever falling off the loop-de-loop.

1. Find the maximum value possible for the radius the loop-de-loop.
2. If the radius of the loop-de-loop is the maximum value found in part (a), find the height at which the puck was released from rest.

Solution

a. The analysis shows that the amount of mechanical energy converted to thermal energy by a single trip across the patch is equal to \(\mu_kmgx\). The puck bounces off the spring once, and makes it around the loop, but never makes it back to the loop after passing over the patch, going up the ramp, and then reentering the patch. The most kinetic energy it can have after passing through the loop-de-loop the second time is therefore the amount of energy converted to thermal after two full trips across the patch:

\[\text{kinetic energy at bottom of loop after bouncing off the spring }=2\mu_kmgx\nonumber\]

The puck must also get around the loop, and the larger the radius of the loop is, the more total energy the puck must have. But we have an upper-limit on the puck's kinetic energy at the bottom of the loop, so this gives us an upper limit on the radius of the loop. From the analysis we found that the puck barely makes it around the loop if its kinetic energy at the bottom of the loop is \(\frac{5}{2}mgR\). Setting this equal to the quantity found above gives us our answer:

\[\frac{5}{2}mgR_{max}=2\mu_kmgx\;\;\;\Rightarrow\;\;\;R_{max} = \frac{4}{5}\mu_kx=\frac{4}{5}\left(0.30\right)\left(80cm\right)=19.2cm\nonumber\]

b. In order for the situation above to occur, the puck must come to rest after passing over the patch exactly three times (once coming down the ramp the first time, then two more times, as described above). Therefore all of the potential energy of the unmoving puck at the release point is converted to thermal energy, and the solution is quick:

\[U_{start} = \Delta E_{thermal} \;\;\;\Rightarrow\;\;\;mgh = 3\mu_kmgx\;\;\;\Rightarrow\;\;\;h=3\left(0.3\right)\left(80cm\right)=72cm\nonumber\]

Problem 3.11

A block slides along a horizontal frictionless surface until it runs into a spring at its equilibrium length.  Just as it starts to compress the spring, the surface becomes rough.

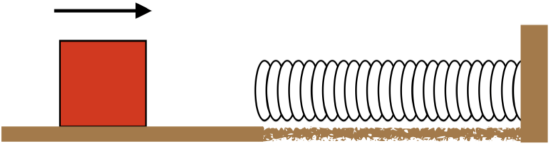
The mass of the block is \(1.2kg\), and it approaches the spring at a speed of \(6.5\frac{m}{s}\). The spring stiffness is \(2.2\frac{N}{m}\), and the coefficient of kinetic friction is a constant value of 0.3. The block eventually comes to rest and remains there.

1. Find the distance that the spring is compressed when the block comes to rest.
2. Find the fraction of the block's kinetic energy that has become thermal by the time the block comes to rest.
3. Find the minimum coefficient of static friction that the rough surface can have.

Solution

a. In the analysis we derived an expression that relates the compression of the spring to all the other quantities:

\[0=\frac{1}{2}m\left(v_f^2-v_o^2\right)+\left(\frac{1}{2}k{\Delta x}^2-0\right)+\mu_kmg\Delta x\nonumber\]

The final speed is \(v_f=0\) and this is a quadratic equation in the value we are looking for (\(\Delta x\)), so the answer is immediate:

\[k\Delta x^2 +2\mu_kmg\Delta x -mv_o^2=0\;\;\;\Rightarrow\;\;\;\Delta x = \frac{-2\mu_kmg\pm\sqrt{4\mu_k^2m^2g^2+4kmv_o^2}}{2k}=\frac{\mu_kmg}{k}\left(-1\pm\sqrt{1+\frac{kv_o^2}{\mu_k^2mg^2}}\right)\nonumber\]

Plugging in the numbers:

\[\Delta x = \left(\frac{\left(0.3\right)\left(1.2kg\right)\left(9.8\frac{m}{s^2}\right)}{2.2\frac{N}{m}}\right)\left(-1\pm\sqrt{1+\frac{\left(2.2\frac{N}{m}\right)\left(6.5\frac{m}{s}\right)^2}{\left(0.3\right)^2\left(1.2kg\right)\left(9.8\frac{m}{s^2}\right)^2}}\right)=3.46m\nonumber\]

b. The thermal energy is the work done by friction:

\[E_{thermal}=\mu_kmg\Delta x = \left(0.3\right)\left(1.2kg\right)\left(9.8\frac{m}{s^2}\right)\left(3.46m\right)=12.2J\nonumber\]

We can also compute the incoming kinetic energy:

\[KE_o=\frac{1}{2}mv_o^2 = \frac{1}{2}\left(1.2kg\right)\left(6.5\frac{m}{s}\right)^2=25.4\nonumber\]

So the fraction of energy converted to thermal is:

\[f = \frac{12.2J}{25.4J}=0.48\nonumber\]

c. The fact that the block has stopped and has not started sliding back means that the net force on the block is zero, which means that the static friction force is equal to the push of the spring. We can compute this force:

\[F=k\Delta x = \left(2.2\frac{N}{m}\right)\left(3.46m\right) = 7.61N\nonumber\]

The maximum static friction force must be this much, so setting the maximum equal to this number gives us the minimum possible coefficient of static friction:

\[\mu_sN=\mu_smg\ge 7.61N\;\;\;\Rightarrow\;\;\;\mu_s\ge \frac{7.61N}{\left(1.2kg\right)\left(9.8\frac{m}{s^2}\right)}=0.65\nonumber\]

Problem 3.12

A particle starts from rest and experiences a net force that has a constant magnitude. This force does change direction, however, such that the particle is made to move in a circular path. Find the power delivered to the particle when it reaches half of its maximum speed, in terms of its mass \(m\), the net force magnitude \(F\), and the radius \(R\) of the circle to which the particle is confined.

Solution

We have an expression for the maximum velocity of the particle from the analysis, so half this amount is:

\[v=\frac{1}{2}\sqrt{\frac{FR}{m}}\nonumber\]

At this speed, the force component that is radially inward to maintain circular motion is:

\[F_{radial}=\frac{mv^2}{R}=\frac{1}{4}F\nonumber\]

The part of the net force that is tangential can then be found using the Pythagorean theorem, as the radial and tangential parts are the two components of the total:

\[F^2=F_{radial}^2+F_{tangential}^2\;\;\;\Rightarrow\;\;\;F_{tangential}=\sqrt{F^2-F_{radial}^2}=\sqrt{F^2-\frac{1}{16}F^2}=\frac{\sqrt{15}}{4}F\nonumber\]

The power delivered is the force component in the direction of motion multiplied by the speed, so:

\[P=\vec F\cdot\vec v = F_{tangential}v=\left(\frac{\sqrt{15}}{4}F\right)\left(\frac{1}{2}\sqrt{\frac{FR}{m}}\right)=\sqrt{\frac{15F^3R}{64m}}\nonumber\]