Sample Problems
- Page ID
- 63407
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)All of the problems below have had their basic features discussed in an "Analyze This" box in this chapter. This means that the solutions provided here are incomplete, as they will refer back to the analysis performed for information (i.e. the full solution is essentially split between the analysis earlier and details here). If you have not yet spent time working on (not simply reading!) the analysis of these situations, these sample problems will be of little benefit to your studies.
Problem 4.1
Two pairs of identical blocks on identical springs are side-by-side as shown in the diagram below. They are set into motion such that just as they reach their (equal) maximum displacements toward each other, they barely come into contact (there is no collision – their springs stop them just as they touch). When they contact, one of the blocks is transferred to the other, and their motion continues.

Explain what happens to the momentum of the four block system shortly after the blocks separate into three and one.
- Solution
-
The momentum of the four block system starts at zero, and at the point when the blocks separate, the two spring forces on the system are equal and in opposite directions, so one might think that the momentum remains zero, because there is no net force on the system. But this doesn't last for long, because the single block starts moving faster than the three blocks, which means that a short time later, the spring of the single block is not stretched as much as the spring for the three blocks. At this moment in time, there is a net force on the 4-block system (to the left), so the momentum will be increasing to the left, due to this net impulse.
Without doing any math, we can see that the forces that act on each side one their way from full stretch to the equilibrium point are the same (they only depend upon the stretch of the spring), but since the three block group takes longer to get to the equilibrium point, is experiences more impulse, which is why the analysis shows that it experiences a greater change in momentum than the single block.
Problem 4.2
Two identical rods of mass \(M\) and length \(L\) have the same non-uniform density profile. When one of these rods is placed along the \(x\)-axis with one end of the rod at the origin, the density as a function of \(x\) is proportional to the following function:
\[\lambda\left(x\right)\propto\left(\frac{x^2}{L^2}+1\right)\nonumber\]
The two rods are laid end-to-end. Describe the possible locations of the center of mass of the two-rod system.
- Solution
-
If the ends of the rods that are connected are of the same density (either both are the less-dense ends, or both are the most-dense ends), then the mass is distributed symmetrically about opposite sides of the connection point of the rods, and the center of mass is right at the connection point. But if the more-dense end of one rod (which we will call rod "A") is connected to the less-dense end of the other rod (rod "B"), then the total mass is not symmetrically-placed across the connection point. In the analysis, we found that the center of mass of each rod is 9/16 of its length from the less-dense end. This means that the center of mass of rod A is at \(x_A=\frac{9}{16}L\), and the center of mass of rod B is at \(x_B=L+\frac{9}{16}L=\frac{25}{16}L\). These two centers of mass are for objects of equal mass, so the center of mass of the system is simply halfway between their centers, which is at:
\[x_{cm}\left(both\;rods\right)=\frac{1}{2}\left(x_A+x_B\right)=\frac{17}{16}L\nonumber\]
So the center of mass is 1/16th of the length of a rod from the connection point, located on the rod whose less-dense end it at the connection point.
Problem 4.3
A child sits on the rear end of a sled (whose mass is uniformly-distributed along its length) with a block of frozen snow at rest in her lap. The sled is sliding forward on the horizontal, frictionless snow at constant a speed, when the child suddenly shoves the block forward in the sled (she remains firmly planted on the sled). After a period of time, the block comes to rest in the front of the sled.
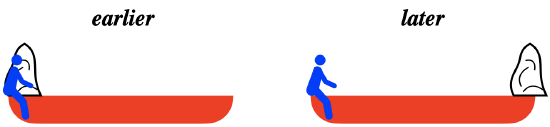
Assume that the mass of the sled is uniformly distributed along its length. Here are the physical properties associated with this situation:
\[\begin{array}{l}\text{mass of child} = 30.0kg && \text{mass of sled} = 12.0kg && \text{mass of ice} = 18.0kg\\ \text{length of sled} = 3.5m && \text{initial speed} = 1.6\frac{m}{s} && \text{time that ice slides} = 2.5s \end{array}\nonumber\]
- Find the speed of the sled after the ice block stops sliding forward.
- Find the position of the center of mass of the child+ sled + block before the block is pushed. Reference this position from the rear of the sled.
- Find the distance (relative to the ground) that the center of mass of the child + sled + block moves during the period of time that the block slides forward.
- Find the distance that the sled moves during the period of time that the block slides forward.
- Solution
-
a. As we stated in the analysis, when all three objects are again moving together, they must have the same speed that they started with, so \(v_f=1.6\frac{m}{s}\).
b. This is just the usual center of mass calculation, and the positions of the child :
\[ x_{cm} = \dfrac{m_cx_c + m_ix_i + m_sx_s}{m_c + m_i + m_s} = \dfrac{0+ 0 + \left(12.0kg\right)\left(1.75m\right)}{30.0kg + 18.0kg+ 12.0kg}=0.350m \nonumber\]
c. The speed of the system remains unchanged during this time (as indicated in part a), so the distance that the center of mass moves during this period is just the speed times the time:
\[ \Delta x_{cm} = v_{cm} t = \left(1.6\frac{m}{s}\right)\left(2.5s\right) = 4.0m \nonumber\]
d. However far the sled travels, the child travels the same distance, and the snow travels that distance plus the length of the sled. Plugging in all these changes into the equation for the change of center of mass (of the whole system) gives:
\[ \Delta x_{cm} = \dfrac{m_c\Delta x_c + m_i\Delta x_i + m_s\Delta x_s}{m_c + m_s + m_s} = \dfrac{m_c\Delta x_c + m_i\left( \Delta x_s+L\right) + m_s\Delta x_s}{M} \nonumber \]
Solving for the displacement of the sled gives:
\[ \Delta x_s = \Delta x_{cm} - \dfrac{m_iL}{M} = 4.0m - \dfrac{\left(18kg\right)\left(3.5m\right)}{60kg} = 2.95m \nonumber \]
Problem 4.4
Two different particles are confined by the same potential, shown in the diagram. Both particles have the same total energy, also depicted in the diagram. At one moment the particles pass each other precisely at the origin, with one particle moving in the \(-x\)-direction and the other moving in the \(+x\)-direction.
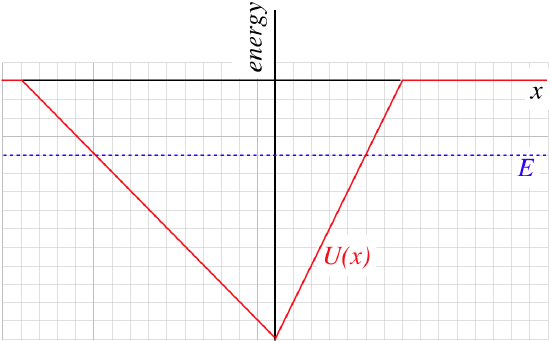
A short time later, both particles come to rest at the same instant. Find the location of the center of mass of the two particles at the moment that they come to rest. Express the answer in terms of the units defined by the grid lines in the diagram.
- Solution
-
In the analysis, we found the ratio of the forces on the two particles. We are told here that the particles take the same period of time to come to rest. If the forces are applied for the same period of time, then the force that is twice as great imparts twice as much impulse on particle B as the lesser force imparts on particle A. Experiencing twice the impulse, the change of particle B's momentum is twice as great. Both particles come to rest, so particle B must start with twice as much momentum as particle A when they are at the origin: \(p_B=2p_A\).
In the analysis we also noted the relationship between momentum and kinetic energy, and reasoned that the particles have the same kinetic energy when they are at the origin. We can therefore draw a conclusion about their masses:
\[{KE}_A={KE}_B\;\;\;\Rightarrow\;\;\;\frac{p_A^2}{2m_A}=\frac{p_B^2}{2m_B}\;\;\;\Rightarrow\;\;\;\frac{m_B}{m_A}=\frac{p_B^2}{p_A^2}=4\nonumber\]
With the relative masses of the two particles now known, all we need is their positions when they come to rest. We can determine this by realizing that at rest they have no kinetic energy, so their total energy equals their potential energy – the points of intersection between the horizontal total energy line and the potential energy curve (which we have previously called the "turnaround points"). So when they come to rest, particle A is at the position \(x=-10\) and particle B is at the position \(x=+5\). Now we just plug into the center of mass formula:
\[x_{cm}=\frac{m_Ax_A+m_Bx_B}{m_A+m_B}=\frac{m_A\left(-10\right)+\left(4m_A\right)\left(+5\right)}{m_A+4m_A}=+2\nonumber\]
So the center of mass moves two units in the \(+x\)-direction in the time that the particles move from the origin to the turnaround points.
Problem 4.5
A block slides along a frictionless horizontal surface at a speed \(v\), starting at position \(x = 0\) and time \(t = 0\). An identical block dropped from rest lands directly on top of it. The surfaces of the blocks are sticky, so the top block adheres to the bottom block when it lands on it, and they continue along together. The blocks slide together into a curtained-off area, during which a spring noise and a “thud” are heard. At a later time, the bottom block emerges from the curtain without the top block on it, after apparently having its top lid sprung open from within.
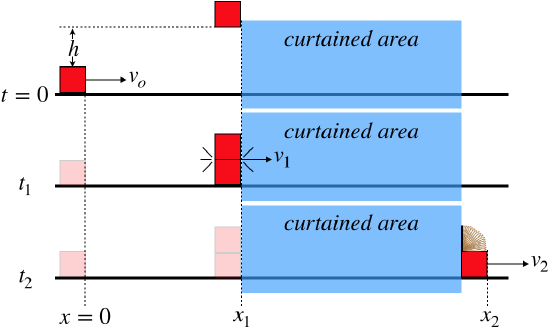
The falling block is dropped at \(t=0\) from a height of \(19.6m\) above the top of the sliding block (the diagram distances are not to scale). The labeled positions are \(x_1=9.6m\) and \(x_2=18.0m\), and the bottom block emerges at time \(t_2=5.0s\). Find the location of the top block at the moment the bottom block emerges from behind the curtain.
- Solution
-
In the analysis we found the velocity of the center of mass of the two block system in terms of the initial velocity of the sliding block, but we are not given that here. We know that the falling block was released from rest at \(t=0\), and how far it drops, so we can compute \(t_1\):
\[h=\frac{1}{2}gt_1^2\;\;\;\Rightarrow\;\;\;t_1=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\left(19.6m\right)}{9.8\frac{m}{s^2}}}=2.0s\nonumber\]
The sliding block travels a known distance in this time, so we can compute its speed:
\[v_o=\frac{x_1}{t_1}=\frac{9.6m}{2.0s}=4.8\frac{m}{s}\nonumber\]
The result from the analysis gives us the center of mass speed:
\[v_{cm}=\frac{1}{2}v_o=2.4\frac{m}{s}\nonumber\]
With the speed of the center of mass of the system we can compute the position of the center of mass when the bottom block emerges. The bottom block spends a time \(t_2-t_1=3.0s\) behind the curtain. At the start of this time span, the center of mass is at \(x_{cm}=x_1=9.6m\), so at the end its position is:
\[x_{cm}=x_1+v_{cm}t_2=9.6m+\left(2.4\frac{m}{s}\right)\left(3.0s\right)=16.8m\nonumber\]
The blocks are equal masses, so their center of mass is halfway between them, giving us the locaton of the top block:
\[x_{cm}=\frac{x_{top}+x_{bottom}}{2}\;\;\;\Rightarrow\;\;\;x_{top}=2x_{cm}-x_{bottom}=2\left(16.8m\right)-18.0m=15.6m\nonumber\]
Problem 4.6
Two blocks slide down opposite sides of a frictionless curved ramp from different heights, colliding at the exact bottom, as shown in the diagram below. Upon colliding, they stick together, and move as a single entity thereafter (if they move at all).
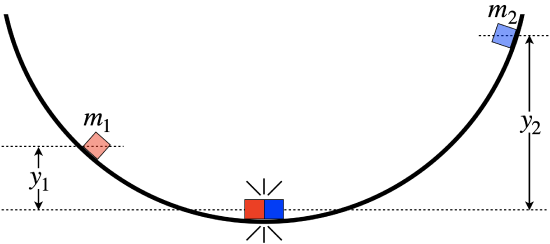
The masses of the blocks are equal, and both blocks are released from rest. After they collide, their center of mass returns to the starting height of the left block.
- Find how many times higher the right block is released than the left block.
- Find the fraction of the original mechanical energy is converted into thermal energy.
- Solution
-
a. The analysis showed that the height the double-block rises before stopping is related to the momentum of the two-block system, which can be determined from the individual momenta of the blocks. So calling the equal masses just "\(m\)", the starting height of the left block "\(h\)", and choosing rightward as the positive direction (so the starting momentum of the right block and final momentum of the two blocks are negative):
\[\left.\begin{array}{l} p_1=\sqrt{2m_1{KE}_1}=\sqrt{2m_1U_1}=m\sqrt{2gh} \\ p_2=-\sqrt{2m_2{KE}_2}=-\sqrt{2m_2U_2}=-m\sqrt{2gy_2} \\ p_f=-\sqrt{2\left(m_1+m_2\right){KE}_f}=-\sqrt{4mU_f}=-2m\sqrt{gh}\\ p_f=p_1+p_2\end{array}\right\}\;\;\; -2m\sqrt{gh}=m\sqrt{2gh}-m\sqrt{2gy_2}\;\;\;\Rightarrow\;\;\;y_2=9h\nonumber\]
b. The original mechanical energy is \(U_1+U_2=mgh+9mgh=10mgh\). After the double-block comes to rest, the mechanical energy of the system is \(U_f=2mgh\). Therefore the percentage of mechanical energy converted to thermal in the collision is:
\[\text{fraction converted} = \frac{10mgh-2mgh}{10mgh} = 0.8\nonumber\]
This is a perfectly inelastic collision, so the reader may be confused about why this fraction is equal to \(0.5\), according to Equation 4.4.3. Be careful! That equation applies specifically to the frame where \(m_1\) is the projectile and \(m_2\) is a stationary target. If we wanted to do lots of extra work, we could change to the rest frame of the left block (making the right block the projectile, which in this frame has all of the system's incoming energy), and use Equation 4.4.3 to obtain the same result.
Problem 4.7
The diagram below depicts a moment just before a collision of two balls made of bouncetech™, a material made by an engineering firm that develops new materials. This experiment was set up as a head-on collision in the center of mass reference frame of the balls. The company's goal is to lose as little kinetic energy as possible to thermal energy in the bounce. To their absolute horror, the two balls stick together! They determine the kinetic energy converted to thermal in this collision to be \(E_o\). They re-check their bouncetech™ formula, and realize that they left out an important ingredient, bounconium. When they repeated the experiment with the corrected mix, they got a much better result.
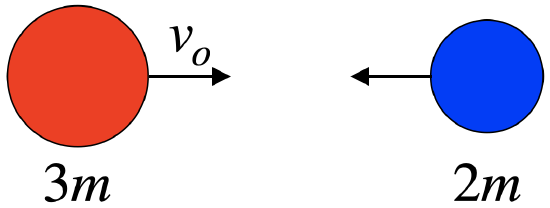
The red ball bounces back with two-thirds the speed at which it came into the collision.
- Find the fraction of kinetic energy that is lost to thermal.
- To please shareholders, the company unscrupulously decides to report to the fraction of kinetic energy lost to thermal as measured in the lab frame where the blue ball was a stationary target. Compute this fraction.
- Solution
-
a. In the analysis we found that the total kinetic energy in the center of mass frame is \(\frac{15}{4}mv^2\). The red ball slows to two-thirds of its initial speed, and since the speeds of the red and blue balls must have the same ratio of speeds to maintain zero system momentum in this frame, it too must bounce away with two-thirds of its initial speed. The kinetic energies of the balls are proportional to the squares of their speeds, so the kinetic energy of both (and therefore their sum) must drop to \(\left(\frac{2}{3}\right)^2=\frac{4}{9}\) of its original value. Thus \(\frac{5}{9}\) of the rest frame kinetic energy is converted to thermal.
b. The actual amount of energy converted to thermal can be computed from the fraction found above:
\[E_{therm}=\frac{5}{9}E_o=\frac{5}{9}\left(\frac{15}{4}mv_o^2\right)=\frac{75}{36}mv_o^2\nonumber\]
The thermal energy converted is the same in any frame, but the combined kinetic energy of the balls in frames other than the center of mass frame is greater, so the ratio of energy converted to thermal is smaller. We determined in the analysis that the blue ball is moving at a speed of \(\frac{3}{2}v_o\), so changing frames to one where it is stationary changes the speed of the red ball to \(v_o+\frac{3}{2}v_o=\frac{5}{2}v_o\), moving to the right. The blue ball contributes no kinetic energy in this frame, so the system's total kinetic energy in this frame is:
\[{KE}_{lab}=\frac{1}{2}\left(3m\right)\left(\frac{5}{2}v_o\right)^2=\frac{75}{8}mv_o^2\nonumber\]
The fraction of energy converted in this reference frame is thus:
\[\frac{E_{therm}}{ {KE}_{lab}}=\dfrac{\frac{75}{36}}{\frac{75}{8}}=\frac{2}{9}\nonumber\]
Losing 22% of its kinetic energy sure looks a lot better in shareholder reports than losing 56% of it!
Problem 4.8
A large sled is at rest on a horizontal, frictionless sheet of ice, when a heavy rock is thrown onto it from behind. The rock is moving purely horizontally when it comes into contact with the sled, and it skids across the rough top surface of the sled until it and the sled are moving forward together at the same speed.

The mass of the rock is 6.5kg, and it is moving at a speed of \(1.8\frac{m}{s}\) when it lands on the \(13.0kg\) sled.
- Find the amount of energy converted to thermal from kinetic.
- Find the ratio of the distance the sled slides on the ice to the length of the rock's skid-mark on the top of the sled.
- Solution
-
a. From the analysis, we have the fraction of the energy converted in this stationary target case, and since we have the rock's mass and initial speed, we know the starting energy, so:
\[E_{thermal}=\left(\frac{m_2}{m_1+m_2}\right)E_o=\left(\frac{m_{sled}}{m_{rock}+m_{sled}}\right)\left(\frac{1}{2}m_{rock}v_o^2\right)=\left(\frac{13.0kg}{6.5kg+13.0kg}\right)\left(\frac{1}{2}\left(6.5kg\right)\left(1.8\frac{m}{s}\right)^2\right)=7.02J\nonumber\]
b. The friction force exerted on the rock is the same magnitude as the friction force exerted on the sled (Newton's 3rd law). The energy converted to thermal is the work done on the rock by friction over the distance of the skid-mark:
\[E_{thermal}= f\Delta x_{skid}\nonumber\]
The work done on the sled by the friction force is its change in kinetic energy, and it starts from rest, so:
\[\frac{1}{2}m_{sled}v_f^2=f\Delta x_{sled}\nonumber\]
Dividing these two equations causes the friction force to cancel out, leaving the ratio we are looking for:
\[\frac{\Delta x_{sled}}{\Delta x_{skid}}=\frac{\frac{1}{2}m_{sled}v_f^2}{E_{thermal}}\nonumber\]
So the ratio we are looking for is the same as the ratio of the thermal energy created to the final kinetic energy of the sled. We can put both of these quantities in terms of the initial energy carried-in by the rock. The relationship between the thermal energy and the initial energy is given above. For the sled's kinetic energy, we use momentum conservation for the perfectly inelastic case that relates the final velocity in terms of initial:
\[v_f=\frac{m_{rock}}{m_{rock}+m_{sled}}v_o\;\;\;\Rightarrow\;\;\;\frac{1}{2}m_{sled}v_f^2=\frac{m_{sled}m_{rock}}{\left(m_{rock}+m_{sled}\right)^2}\left(\frac{1}{2}m_{rock}v_o^2\right)=\frac{m_{sled}m_{rock}}{\left(m_{rock}+m_{sled}\right)^2}E_o\nonumber\]
Now form the ratio, and perform algebra:
\[\frac{\Delta x_{sled}}{\Delta x_{skid}}=\dfrac{\frac{m_{sled}m_{rock}}{\left(m_{rock}+m_{sled}\right)^2}E_o}{\left(\frac{m_{sled}}{m_{rock}+m_{sled}}\right)E_o}=\frac{m_{rock}}{m_{rock}+m_{sled}}=\frac{1}{3}\nonumber\]
So the sled slides along the ice a distance that is one third the length of the skid-mark.
Problem 4.9
A cart slides along a frictionless surface in an easterly direction. The cart contains a person and a medicine ball. The cart slides past an identical (but empty) stationary cart, also on the frictionless surface. When the carts are side-by-side, the person throws the medicine ball into the other cart by pushing the ball in the north direction.
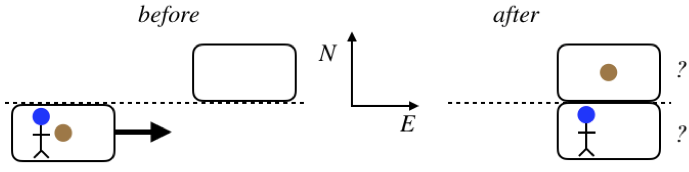
Both carts have masses of \(100kg\), the person's mass is \(60.0kg\), and the medicine ball has a mass of \(15.0kg\). The speed of the cart before is \(2.40\frac{m}{s}\). The person sees the ball move away from them at a speed of \(3.20\frac{m}{s}\), and it comes to rest inside the other cart. Find the speed and direction of both carts after the medicine ball has been exchanged. Express the directions as angles that are north or south (indicate which) of east.
- Solution
-
We'll start with what we know immediately – the \(x\)-component of the velocity of cart #1 never changes, since the ball is thrown in the \(y\)-direction:
\[v_{1x}=v_o=2.40\frac{m}{s}\nonumber\]
We anticipated this in the analysis – the relative motion of the person and medicine ball are given. We'll start by computing the \(x\)-component of the motion of cart #2 + ball. We can do this because we know that the ball does not change its \(x\)-component of velocity after being pushed:
\[m_{ball} v_o = \left(m_{ball} + m_{cart} \right)v_{2x} \;\;\;\Rightarrow \;\;\; v_{2x} = \left(\frac{m_{ball}}{m_{ball} + m_{call}}\right)v_o =\left(\frac{15.0kg}{15.0kg + 100kg}\right)\left(2.40\frac{m}{s}\right)= 0.313 \frac{m}{s} \nonumber \]
As we found in the analysis:
\[0 = m_{ball}v_b+\left(m_{cart}+m_{person}\right)v_p\nonumber\]
We are not given \(v_b\) (which is the \(y\)-component of the ball's velocity relative to the Earth), but we can write it in terms of person's \(y\)-component of velocity \(v_p\) and the relative speed \(v_{bp}\), as we did in the analysis:
\[v_b=v_{bp}+v_p\nonumber\]
Plugging this in above gives us the \(y\)-component of the person + cart 1:
\[\begin{array}{l} 0 = m_{ball}\left(v_{bp}+v_p\right)+\left(m_{cart}+m_{person}\right)v_p \\ \Rightarrow \;\;\; v_{1y}=v_p=-\left(\frac{m_{ball}}{m_{ball}+m_{person}+m_{cart}}\right)v_{bp}=-\left(\frac{15.0kg}{15.0kg+60.0kg+100kg}\right)\left(3.20\frac{m}{s}\right)=-0.274\frac{m}{s}\end{array}\nonumber\]
With the two components of the final velocity for cart 1 now known, we can write its magnitude and direction:
\[v_1=\sqrt{v_{1x}^2+v_{1y}^2}=\sqrt{\left(2.40\frac{m}{s}\right)^2+\left(-0.274\frac{m}{s}\right)^2}=2.42\frac{m}{s}\nonumber\]
\[\theta_1=\tan^{-1}\left(\frac{-0.274}{2.40}\right)=6.51^o \text{ south of east}\nonumber\]
Now we turn to cart 2 + ball. We have already solved for the \(y\)-component of velocity for cart 1 + person, and since the total system started with no total momentum in the \(y\)-direction, cart 2 + ball must have a momentum that cancels that of cart 1 + person:
\[\left(m_{cart}+m_{ball}\right)v_{2y}=\left(m_{cart}+m_{person}\right)v_{1y}\;\;\;\Rightarrow\;\;\;v_{2y}=\left(\frac{100kg+60.0kg}{100kg+15.0kg}\right)\left(0.274\frac{m}{s}\right)=0.381\frac{m}{s}\nonumber\]
We already have the velocity of cart 2 in the \(x\)-direction, so we put it together with this \(y\) direction result to get our answers:
\[v_2=\sqrt{v_{2x}^2+v_{2y}^2}=\sqrt{\left(0.313\frac{m}{s}\right)^2+\left(0.381\frac{m}{s}\right)^2}=0.493\frac{m}{s}\nonumber\]
\[\theta_2=\tan^{-1}\left(\frac{0.381}{0.313}\right)=50.6^o \text{ north of east}\nonumber\]


