2.5: Spring-Mass Oscillator

Last updated
Save as PDF

Page ID: 19098

This page is a draft and is under active development.

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Spring-Mass Force

Take a look at the three scenarios depicted below for a horizontal spring-mass system. In picture A) the spring-mass is at its equilibrium position (x=0), which means that it is not experiencing a net force. The equilibrium position is where the spring-mass system "wants" to naturally be. When the mass is displaced from the equilibrium, the force, known as restoring force, will always point back toward equilibrium. In picture B) the spring is compressed and the force pushes the mass back toward equilibrium, where in picture C) the spring is stretched, and the restoring force pulls the mass back to the left.

Figure 2.5.1: forces experienced by a spring-mass system.

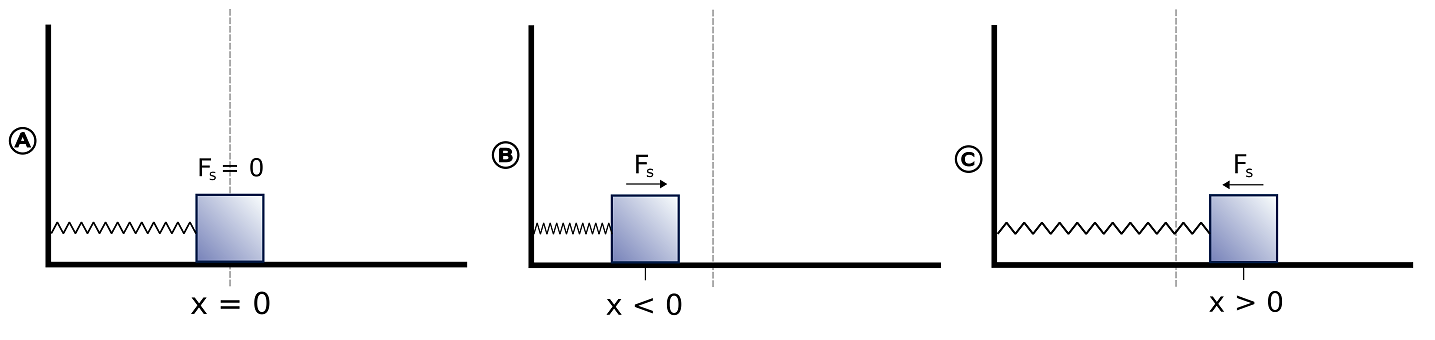
2000px-Harmonic_oscillator.svg.png

The force with which a spring pulls back when stretched (or pushes back when compressed) is proportional to the amount of stretch from equilibrium, provided the spring is not stretched too far. Historically, this linear proportionality between the force and amount of stretch is referred to as Hooke’s Law behavior, which is true if the mass of the spring is negligible. We write the restoring force as:

\[F = -k x\]

where k is the “spring constant” or “force constant” (and depends on the stiffness of the particular spring), and x is the displacement from equilibrium. The minus sign indicates that the force is the opposite direction to the direction the spring was stretched or compressed. In other words, if you are applying a force on the spring-mass that displaces it from equilibrium, the restoring force will act in the opposite direction of the applied force. An important point to notice in the expression for the force of the spring is that x is measured from the un-stretched position of the free end of the spring.

In order for the force to have units of newtons, the units of k must be newtons per meter (N/m). The force that you (an external agent) have to exert on the spring to stretch it a distance \(x\) is in the opposite direction to the restoring force and is equal to \(F_{applied}=+k x\).

Hooke's Law breaks down at the extremes of a spring's motion. For example, when stretched to the point of breaking or permanent deformation, a spring's behavior will begin to deviate substantially from the linear expectation. Also, when compressed so far that it begins to touch itself, and the forces at play change. For these reasons, it is usually assumed that springs stretch only within a small portion of their maximum deformation.

Spring-Mass Potential Energy

Let us refer back to Figure 2.3.4. Work is done when the mass is pulled away from equilibrium. Assuming the kinetic energy stays constant (spring-mass is motionless at equilibrium and held in place when stretched), the work done contributes only to increasing the potential energy of the spring-mass system. We call this type of energy, the spring-mass potential energy, \(P_{sm}\). The change in potential energy depends on the amount of work done. Work is proportional to force which depends on the distance away from equilibrium. This suggests that the indicator for \(P_{sm}\) is displacement from equilibrium, denoted by d or |x| or sometimes |y| for vertically hanging springs. Note, the absolute value sign around "|x|" implies that the potential energy does not depend on whether the spring is compressed or stretched, since Hooke's Law is symmetric about the equilibrium position. Assuming the spring-mass is stretched a distance d from equilibrium, the Energy-Interaction diagram for the interval depicted in Figure 2.3.4 is:

Figure 2.5.2: Energy-Interaction diagram for stretching a spring-mass system.

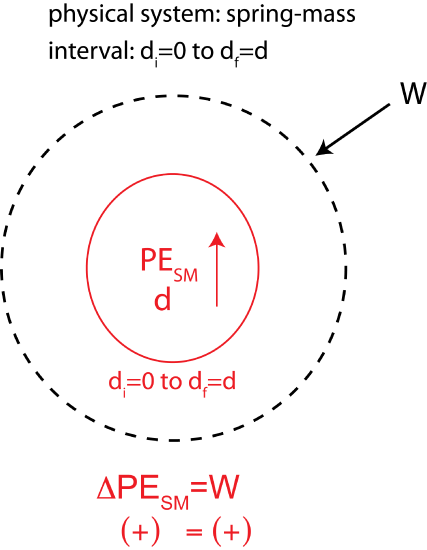
The restoring force, \(F = -kx\), is not constant since it depends on displacement x. That is, the force is proportional to the distance the spring has been pushed or pulled. So we can no longer used the simplified version of work, but will use the general Equation 2.3.1 for work. The applied force does work when the spring is stretched from distance of zero to a max of d, in this example. Thus, the work done on this system:

\[W = \int \limits_0^d kxdx= \dfrac{1}{2}kd^{2}\]

Notice that while the force scales linearly with deformation, the work required to deform the spring scales as the square of deformation. This also confirms that the potential energy will depend on the magnitude of the displacement only, and not the direction. Using the energy-conservation equation from Figure 2.5.2 we get \(\Delta PE_{sm}= \dfrac{1}{2}kd^{2}\). Generally, the spring-mass potential energy is given by:

\[PE_{sm} = \dfrac{1}{2}kx^{2}\]

where x is displacement from equilibrium. Upon stretching the spring, energy is stored in the springs' bonds as potential energy. This potential energy is released when the spring is allowed to oscillate. The maximum speed is accomplished when the spring returns to its equilibrium position (PE_sm=0), and all energy is kinetic energy.

Example \(\PageIndex{1}\)

A spring of negligible mass and a spring constant of 120 N/m is fixed to a wall and is free to oscillate. On the other end, a ball with a mass of 1.5 kg is attached. The spring-mass is then stretched 0.4 m and released.

a) What is the maximum speed of the attached ball? Neglect any effects of friction.

b) The spring-mass looses 2 Joules of energy per oscillation. Find the maximum displacement of the spring-mass after 4 oscillations.

Solution

a) Let us focus on the interval once the ball is released until it is at equilibrium when the speed is maximum.The spring-mass system is closed since it is not interacting with other systems in this interval. As the spring-mass oscillates potential and the kinetic energies change, \(\Delta E_{tot}= \Delta PE_{sm}+\Delta KE=0\). The Energy-Interaction Diagram for this process is shown below:

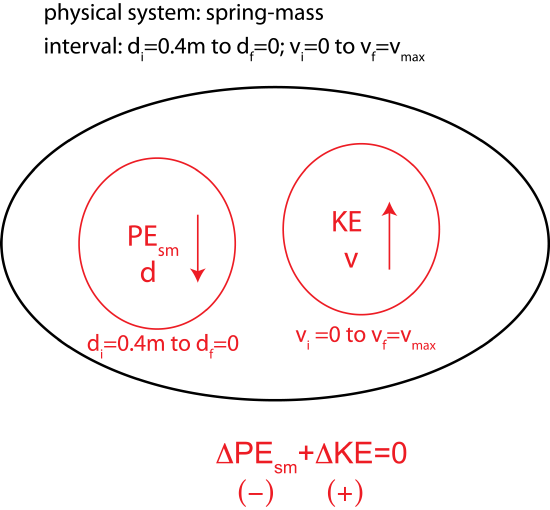
Using definitions of potential and kinetic energies:

\[\frac{1}{2}k(x_f^2-x_i^2)+\frac{1}{2}m(v_f^2-v_i^2)=0\nonumber\]

Plugging in values into the equation:

\[\frac{1}{2}(120 N/m)(0-0.4^2m^2)+\frac{1}{2}(1.5 kg)(v_{max}^2-0)=0\nonumber\]

and solving for \(v_f\), we get \(v_f=3.58 m/s\).

b) In 4 oscillations the spring-mass will loose 8 Joules. Let's choose an interval from initial maximum displacement of 0.4m to the final maximum displacement after 4 oscillations. Since the speed is zero when the displacement is maximum, there will be no change in kinetic energy over this interval. The Energy-Interaction Diagram for this process is shown below:

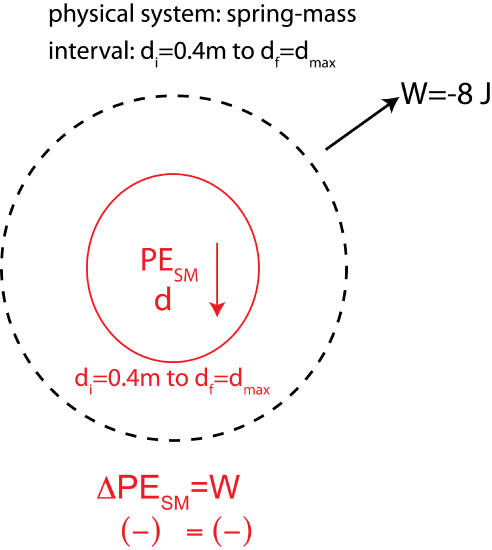
The equation can be rewritten as:

\[\frac{1}{2}k(d_f^2-d_i^2)=W\nonumber\]

Plugging in values into the equation:

\[\frac{1}{2}(120 N/m)(d_{max}^2-0.4^2m^2)=-8 J\nonumber\]

Solving for \(d_{max}\), we find the maximum displacement after 4 oscillations to be 0.16m.

Vertical Spring-Mass Systems

A spring with a mass hanging down acts exactly like a horizontal spring, except that the end of the spring has a different equilibrium position. For a vertically hanging spring-mass there are two forces acting on the mass as it oscillates: the force from the spring pulling up or pushing down, and the force from the Earth always pulling down. Let us take a closer look why the horizontal and vertical spring-mass systems can still be treated identically.

For the vertical spring (as for the horizontal one), the force with which a spring-mass pulls back when stretched (or pushes back when compressed) is proportional to the amount of stretch from the equilibrium determined with the mass attached (provided the spring is not stretched too far). For a vertical spring, we will usually write the restoring force using the symbol “y” instead of with an “x”, but this is just a convention:

\[F = -k y\]

Similarly to the horizontally attached spring in Example 2.5.1, let us analyze a situation of finding the maximum speed of the mass at equilibrium. In the example, we found the following general equation for an interval when the mass is released from maximum displacement to its equilibrium position, assuming thermal dissipation is negligible:

\[\frac{1}{2}kx_{max}^2=\frac{1}{2}mv_{max}^2\label{energy.SM}\]

Let us now see what we get for a vertical spring given the same interval. We will start by measuring the potential energy of this system from (y=0) in the figure below, the equilibrium position of the spring without the mass attached.

Figure 2.5.3: Vertical spring-mass system.

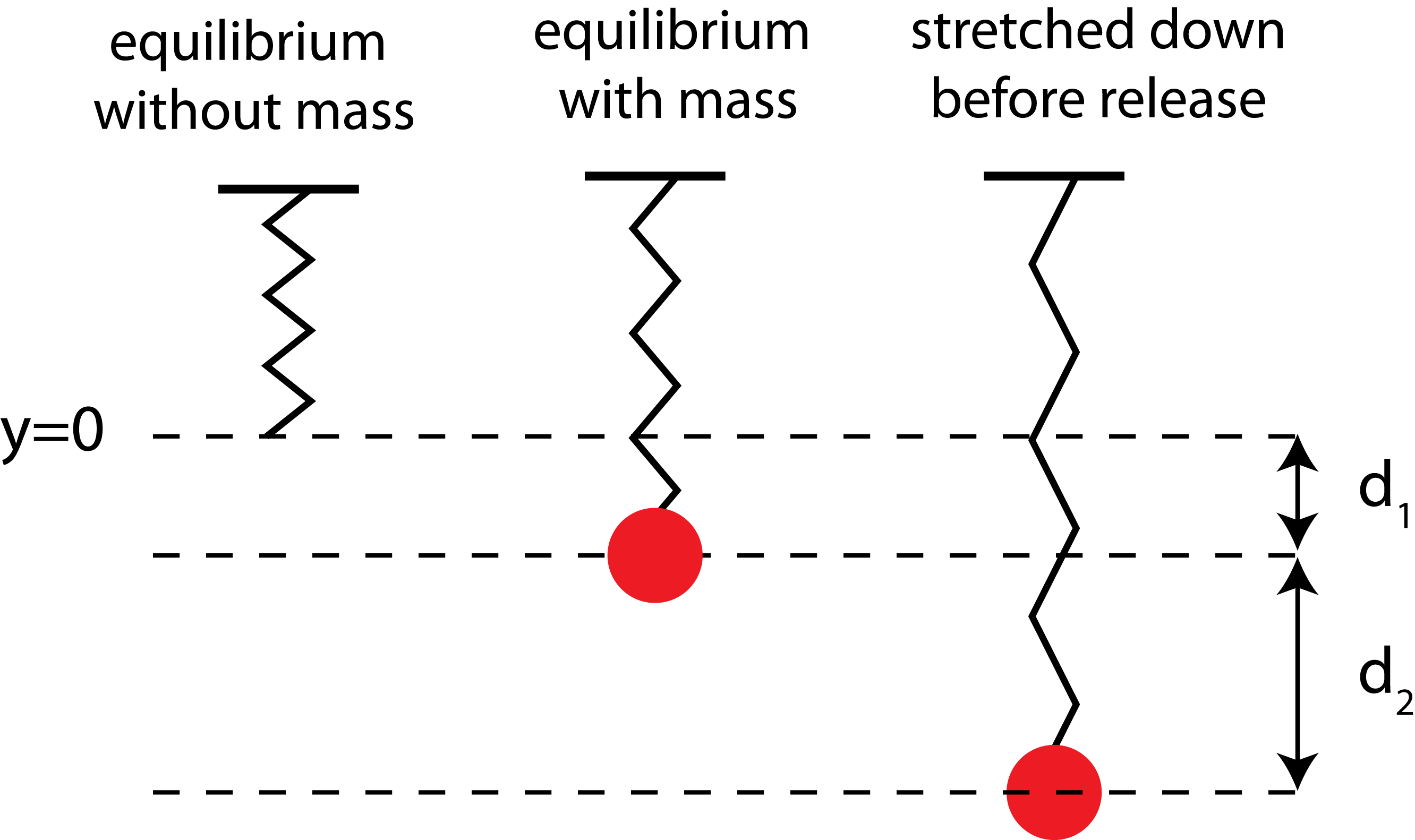
When the mass is initially attached it stretches by a distance \(d_1\) to a new spring-mass equilibrium. At this position the spring-mass is not moving, so the forces acting on it must be balanced. That is, the gravitation force must be equal and opposite to the spring-mass restoring force:

\[mg=kd_1\label{forces.vertical.SM}\]

The spring-mass is then stretched another distance \(d_2\), released, and allowed to oscillate. Recall, all the vertical heights used in calculating PE_gare measured from the y=0 defined in Figure 2.5.3. Thus, the values of y for the equilibrium and stretched positions (center and right configurations in the figure) will be negative. The Energy-Interaction Diagram for calculating the maximum speed when the spring-mass returns back to equilibrium after release is shown in the figure below.

Figure 2.5.4: Energy-Interaction diagram for a vertical spring-mass system.

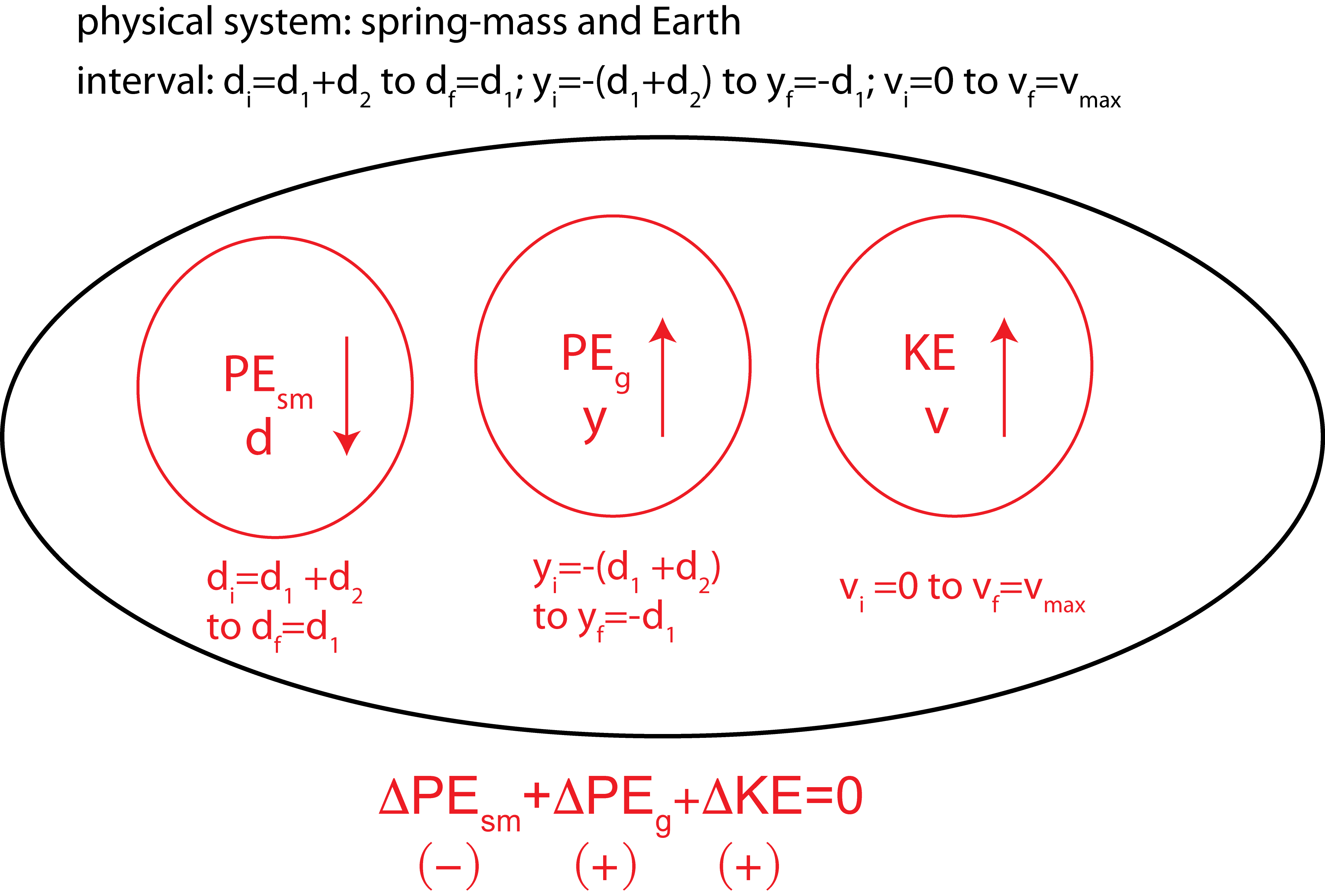
Expanding the equation from the Energy-Interaction diagram and plugging in the variables for the energy indicators:

\[\frac{1}{2}k(d_f^2-d_i^2)+mg(y_f-y_i)+\frac{1}{2}m(v_f^2-v_i^2)=0\]

\[\frac{1}{2}k(d_1^2-(d_1+d_2)^2)+mg(-d_1+d_1+d_2)+\frac{1}{2}m(v_{max}^2-0)=0\]

Simplifying:

\[-\frac{1}{2}kd_2^2-kd_1d_2+mgd_2+\frac{1}{2}mv_{max}^2=0\]

Using Equation \ref{forces.vertical.SM} for d₁, the equation simplifies further to:

\[-\frac{1}{2}kd_2^2+\frac{1}{2}mv_{max}^2=0\]

The above equation is identical to the horizontal spring-mass result in Equation \ref{energy.SM}, as long as the displacement for the vertical spring-mass is measured from the new equilibrium position once the mass is attached to the spring.

Alert

The result above shows that when a spring-mass is vertically attached the effect of the gravitation force is automatically taken into account, as long as the new equilibrium position is defined at the position of the spring with the mass attached. Using the new equilibrium position the potential energy of the spring-mass is described by the behavior of the spring-mass oscillator only. Imagine if the spring-mass system was far in outer space away from gravity, mounted on a wall of a spaceship. The spring-mass would still oscillate, but the orientation of "horizontal" vs. "vertical" would lose its meaning.

Contributors

Authors of Phys7A (UC Davis Physics Department)