7.2: Applications of Momentum Conservation
( \newcommand{\kernel}{\mathrm{null}\,}\)
Collisions
Types of interaction where analysis of momentum is applied are known as collisions. But the word "collision" should not be taken literally. From a physics perspective it means an interaction between objects. When you throw a ball, we can study the change of momentum of you and the ball since an interaction occurred, but you would not call this event a "collision" in daily language. But in physics we clump all these interactions as "collisions" when we want to analyze momentum. A collision can involve one object which defines a system colliding with some external object from the environment or it may involve collisions of two or more objects.
We want to analyze momentum conservation in the interval before and after the collision, similarly to the way we studied conservation of energy over some interval by comparing the initial and final energies. Once a physical system is defined one can determine whether the momentum will be conserved after a collision by observing whether external forces act on the system during that interval. If there are no net force or a negligible net force, then momentum will be conserved. Otherwise, the momentum of the system will change. The reverse is also true, if information about external forces is not known but momentum before and after the collision is measured, one can determine whether an external net force was present by comparing initial and final momentum of the system.
The next question we would like to ask is what happens to energy during a collision, specifically the kinetic energy of the system. We learned from 7A that mechanical energy can be converted to thermal energy. For example, when a object falls to the ground and comes to rest, its initial potential energy at some height is converted to kinetic energy as it falls, and then to thermal energy when it hits the ground. However, a very elastic ball could bounce back up with kinetic energy almost exactly the same as the kinetic energy it had before hitting the ground. In this case kinetic energy is conserved, since no mechanical energy is converted to thermal.
Thus, another piece of information about collisions which is important is the conservation of kinetic energy. If the collision is between two protons or two billiard balls, kinetic energy might be exactly or almost conserved. Collisions in which kinetic energy is conserved are called elastic collisions. In most types of collisions, however, the interaction between two objects results in some sort of deformation or friction between them converting some of kinetic energy to internal energy, which could be either thermal energy resulting in a rise of temperature or bond energy in a case when bonds are broken. These types of collisions are known as inelastic collisions. Below we will look at multiple example of different types of collisions. We will analyze system that consist of one object and multiple object. At first we will focus on one-dimensional collisions, and then we will expand our analysis to two-dimensional events.
One-Body Systems
A example of a system which consists of one object is shown below in Figure 7.2.1. In this scenario a cart moving to the right with initial velocity, vi, collides with the wall after which it is moving to the left with some final velocity, −vf. Note, in one-dimensional problems when vector quantities are involved, typically the arrow above the vector quantity is dropped, and only the signs in front of the vector quantity, plus or minus, are used to specify the direction for a given convention. In this case for velocity of a cart whose motion is in one-dimension, it can only move to the right or to left, and our convention states that velocity to the right is positive, and to the left it is negative.
Figure 7.2.1: One Cart Collision
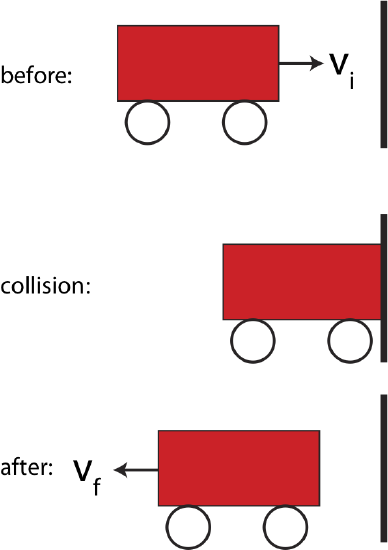
We define the physical system here as the cart. Since the direction of its motion changed, regardless of the magnitude of the speed after the collision, the cart's momentum is not conserved. Momentum is a vector quantity which is proportional to velocity, so even if the cart bounced back with the same speed, the direction changed, so did the momentum. Another reason why we know that momentum changed is that there was an external force during this interval which was exerted on the cart by the wall during the collision. The force is external since the wall is not included in our physical system. Mathematically, applying the impulse-momentum model from the previous section to this situation, we get:
Jext=mΔv=−mvf−mvi
To analyze conservation of kinetic energy, we need to compare the difference between initial and final energies:
ΔKE=KEf−KEi=12mΔ(v2)=12mv2f−12mv2i
Let us now examine different cases of this type of collision.
Case 1: Elastic Collision
Assume that the cart from Figure 7.2.1 bounced back to the left with the same speed as its initial speed, which is define as speed, v:
v≡|vi|=|vf|
Perhaps this happened because there is a spring attached to the cart which compressed during the collision, converting kinetic energy to spring energy, and then converting back to kinetic energy as the spring returns to equilibrium when the cart separates from the wall. Thus, we are assuming negligible conversion of mechanical energy to thermal energy. Thus, for this case, equation ??? becomes:
Jext=mΔv=m(−v)−mv=−2mv
The result above tells us that the momentum of our system is not conserved and is equal to the external impulse which points to the left and has a magnitude of 2mv. We often depict collision problems with a momentum chart. Momentum charts are a visualization tool which demonstrates the collision geometrically using arrows to represent momentum vectors. This tool will be especially useful when dealing with systems which consist of two or more objects, when algebra become more cumbersome and the momentum chart can act as a good tool to check for mathematical errors. Figure 7.2.2 below depicts a momentum chart for our case 1.
Figure 7.2.2: Momentum Chart One Cart Elastic Collision
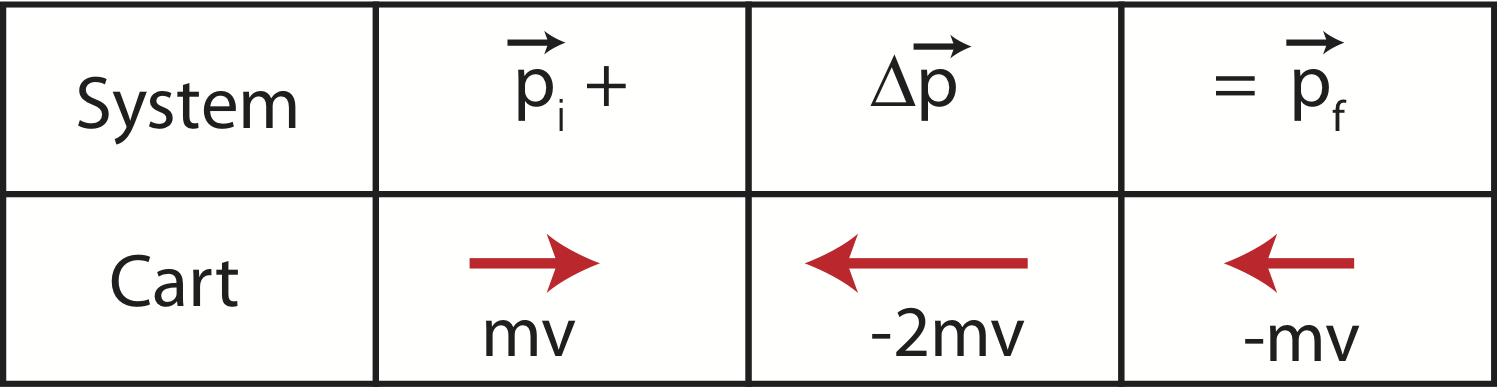
The momentum chart shows a connection between the initial and final momenta by converting difference to two vectors, Δ→p=→pf−→pi, into a sum, →pi+Δ→p=→pf. The arrows depict both the direction (right or left), and the magnitude, since the arrow for Δ→p is drawn twice as long. Below the arrows the algebraic expressions are written. Depending on the purpose of using a momentum chart algebraic expressions are not always shown.
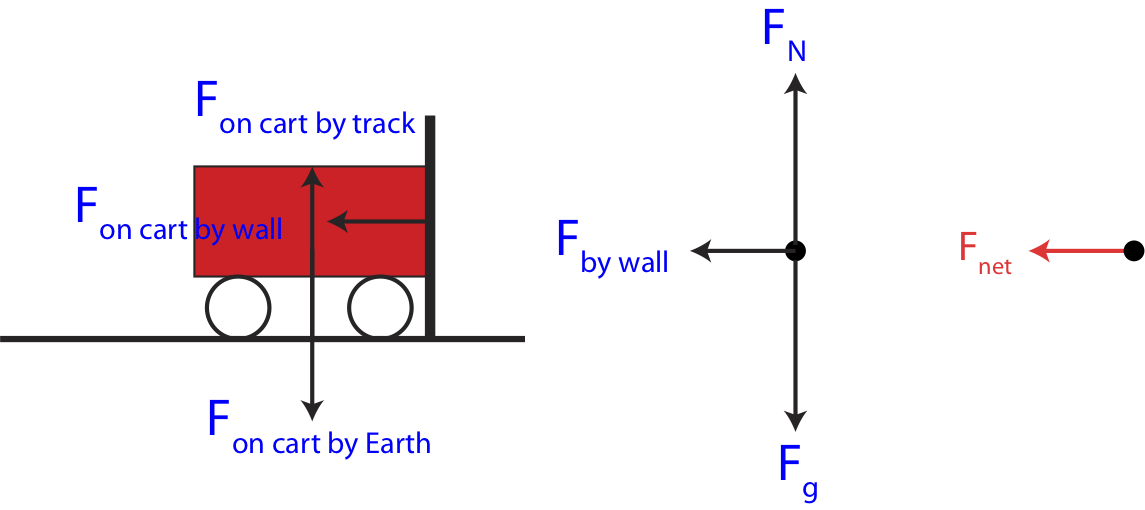
Equation ??? shows that the external impulse which equals to the change in momentum has twice the magnitude and points in the opposite direction of initial momentum. A force diagram (or FBD) is also a useful tool for explaining the conservation of momentum for a given situation. Figure 7.2.3 below shows the forces that act on the cart during the collision. The leftmost figure below shows the cart all the forces that act on the cart at different locations. The forces are labeled with the "on by" notation. The middle figure is a FBD, where the central dot represents the cart, and the force labels are abbreviated with their standard notations. The leftmost diagram shows the net force, which is the sum of all the forces. The forces in the y-direction cancel since there is no change in momentum in that direction. Thus, the only remaining force is the force by the wall, which is the net force.
Figure 7.2.3: FBD for a One Cart Collision
Let us now check what type of collision this is by looking at conservation of energy. Kinetic energy is a scalar quantity independent of direction of motion, so only the magnitude of velocity, the speed, of the system before and after the collision will matter. Using Equation ??? and plugging in values of velocity for case 1 we get:
ΔKE=12mv2−12mv2=0
Since kinetic energy is conserved, case 1 describes an elastic collision.
Case 2: Inelastic Collision
For the next scenario, let us assume that after the collision the cart is traveling with half of its initial speed:
v≡|vi|=2|vf|
For this case equation ??? becomes:
Jext=mΔv=m(−v2)−mv=−32mv
The momentum chart for this scenario will have the same directions but different magnitudes of momentum, as shown below.
Figure 7.2.4: Momentum Chart One Cart Inelastic Collision
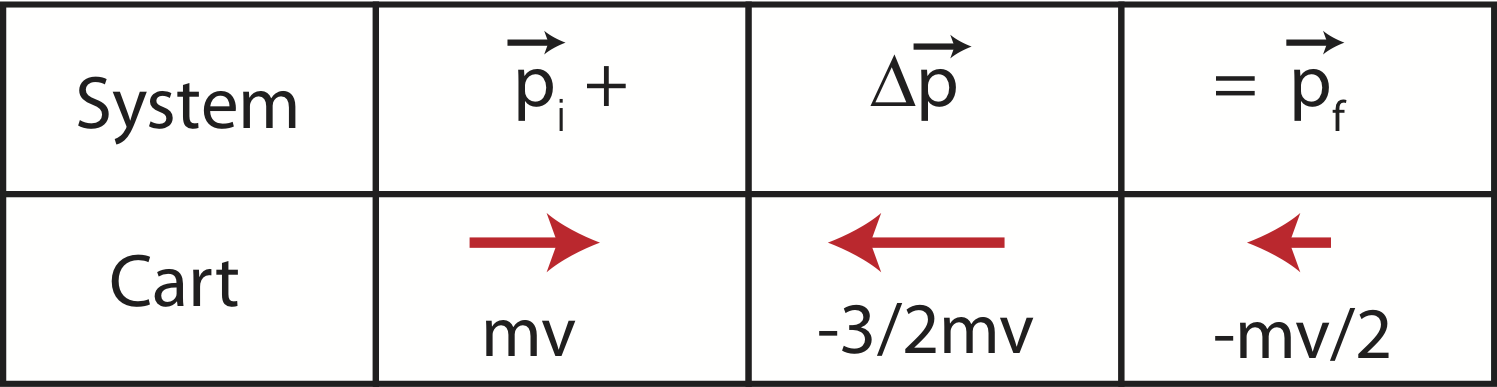
In this case the change in kinetic energy is no longer zero. Plugging velocity values into Equation ??? we get:
ΔKE=12m(v2)2−12mv2=−38mv2
Since kinetic energy is not conserved, case 2 describes an inelastic collision. The loss of kinetic energy is converted to thermal energy which represents the increase in the random motion of particles in the wall and the cart due to the collision.
Example 7.2.1
A 0.4 kg ball is moving down at 5 m/s before it hits the floor. It bounces back up with kinetic energy of 0.8 J. Answer the following questions:
a) Is this collision elastic or inelastic? If kinetic energy is not conserved, what is the change in thermal energy during the collision?
b) Is momentum conserved? If not, calculate the total impulse on the ball during the collision with the floor.
- Solution
-
To check whether the collision is elastic or inelastic, we need to calculate the change in kinetic energy.The initial kinetic energy is:
KEi=12mv2i=12(0.4kg)(5m/s)2=5J
Since the final kinetic energy is less than 5 J, it is not conserved and the collision is inelastic. The decrease in kinetic energy is equal to the increase in thermal energy, since total energy is conserved:
ΔKE+ΔEth=0
ΔKE=KEf−KEi=0.8J−5J=−4.2J,
so the increase in thermal energy is 4.2 J.
b) Momentum is not conserved since the ball changes its velocity, both the speed and direction are different after the collision. From kinetic energy we can find the final speed:
vf=√2KEfm=√2×0.8J0.4kg=2m/s
The change in momentum will equal to the impulse on the ball:
J=Δp=mvf−mvi=0.4kg[2m/s−(−5m/s)]=2.8Ns
In the equation above, we defined up as the positive direction and down as negative, such that the initial velocity is - 5 m/s and the final velocity is + 2 m/s. The net impulse is in the positive direction, since it is due to the force by the floor pushing on the ball in the positive upward direction.
Multiple-Body Systems
Another very common category of momentum conservation problems is studying collisions between multiple objects, such as billiard balls, asteroids in space, or even automobile crashes. Often there are external forces acting on these multiple-body system, such as friction with the road or track, or gravity. However, often the effects of the collision are dominant during a short time scale immediately after the collision, and the effects of forces such as friction can be neglected over a short time-frame. Thus, we often idealize these situation and assume the momentum of the system is conserved. Of course, if we are discussing asteroids colliding in empty outer space this is already an ideal situation where no external forces are present.
Case 1: Two-body Elastic Collision
Figure 7.2.5 below shows example of a two-body cart elastic collision. We assume that no external forces act on the two carts, and both carts have the same mass, m. Cart A is initial moving to the right with speed v while cart B is stationary. After the collision, cart A stops and transfers all of its momentum to cart B which moves to the right with the same speed v.
Figure 7.2.5: Two-Body Elastic Collision
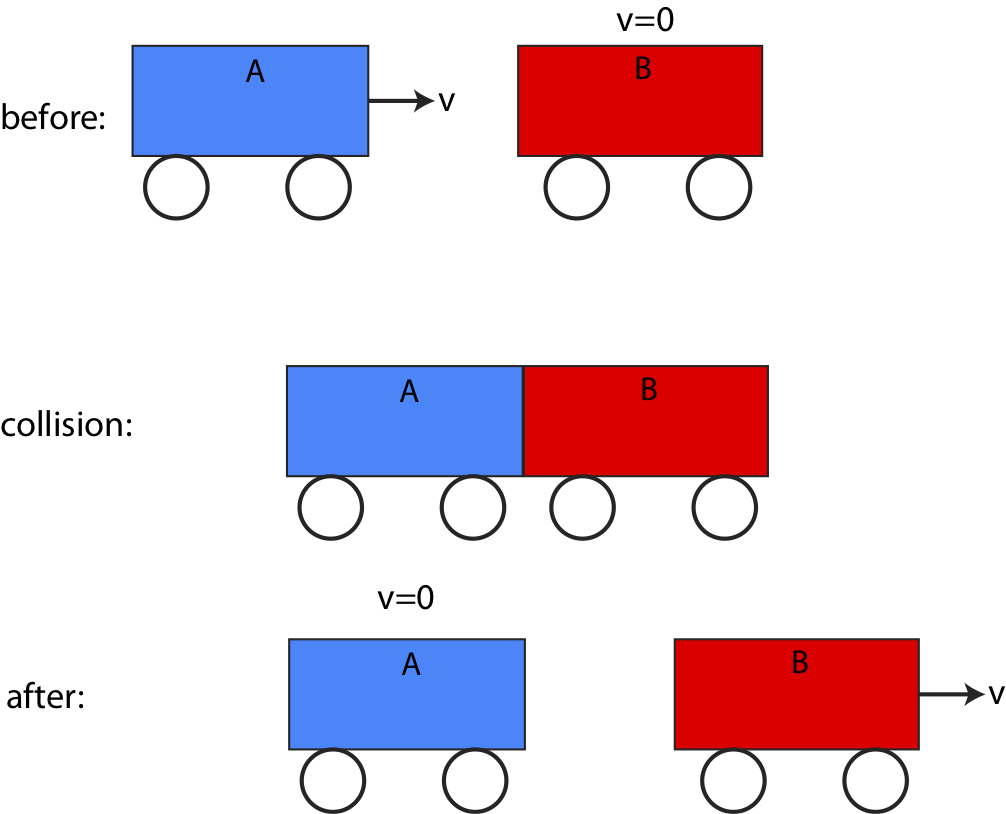
Momentum is conserved because the initial momentum of the system equals to the final momentum of the two cart system:
pi,tot=mvi,A+mvi,B=mv+0
pf,tot=mvf,A+mvf,B=0+mv
Thus,
pi,tot=pf,tot
The collision is elastic since kinetic energy is also conserved:
KEi,tot=KEi,A+KEi,B=12mv2+0
KEf,tot=KEf,A+KEf,B=0+12mv2
Resulting in
KEi,tot=KEf,tot.
The momentum chart below depicts this scenario using vector notation.
Figure 7.2.6: Two-Body Elastic Collision Momentum Chart
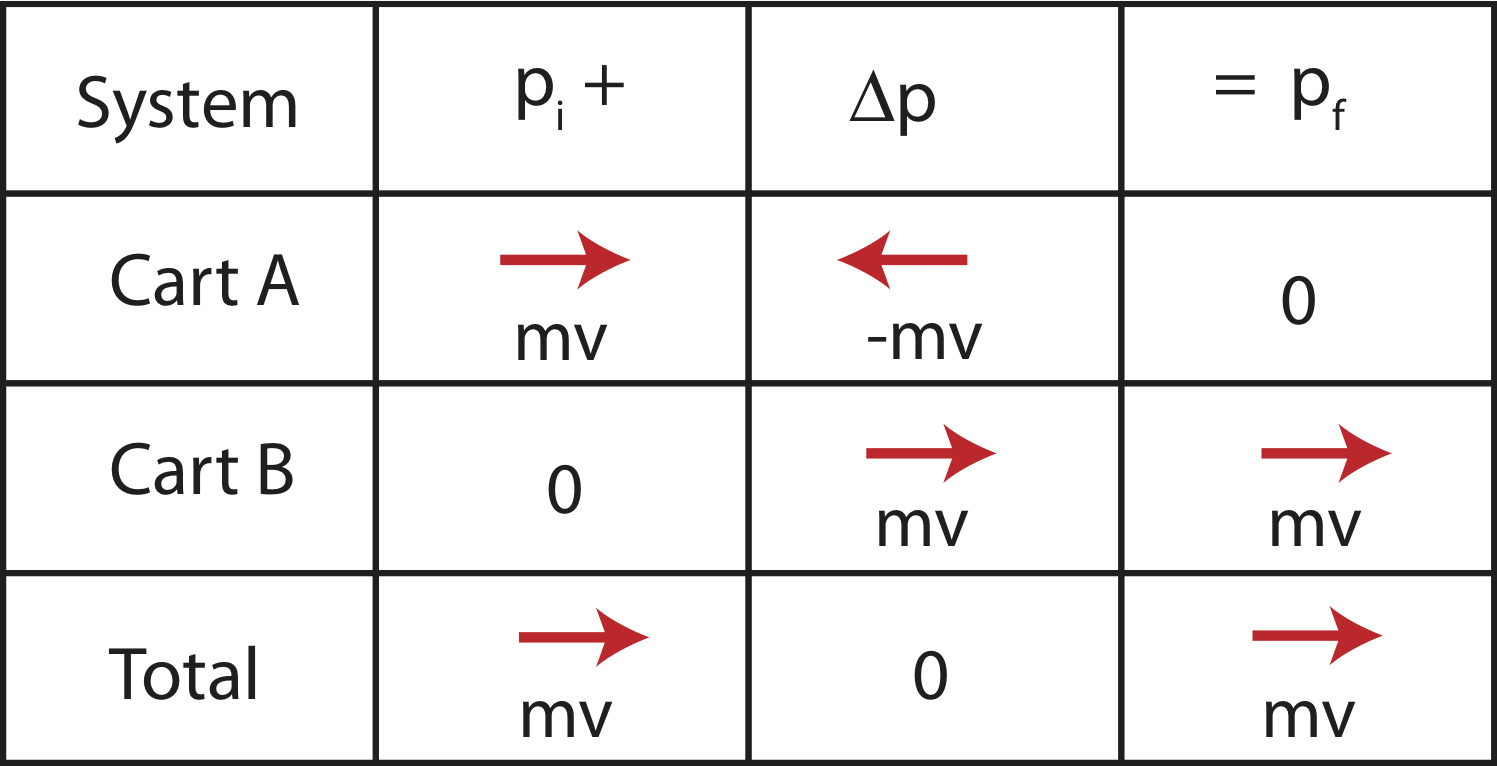
This momentum chart now has three rows, one for each object in the system and the third for the total momentum of the system. For multiple-object momentum charts, not only the first two entries in each row must add up to the third entry in a given row, the same is true for columns. When two objects describe the system, the first two entries in each column add up to the last entry in column, labeled "total". The quantity Δp in the last row represents the total change in momentum of the system. When it is zero, as in this example, it shows that the system's total momentum is conserved implying that no net external impulse acts on the system, even though the momentum of individual objects that define the system can change.
Case 2: Two-body Inelastic Collision
In an inelastic collision between two objects kinetic energy is not conserved, so we can not equate initial and final kinetic energies. A standard inelastic collision between two objects involves them colliding and changing their momentum after the collision which results in some loss of kinetic energy. An interesting case occurs when the collision is when the objects stick together during the collision, and thus both have the same final velocity after the collision. This is known as a perfectly inelastic collision. An example is shown in Figure 7.2.7 below. In this scenario we also look at a case of having different masses. Cart B is three times heavier than cart A. Initially, cart A is moving to the right with speed v and collides with a stationary cart B. The two carts stick together and move to the right with some final speed vf.
Figure 7.2.7: Two-Body Inelastic Collision
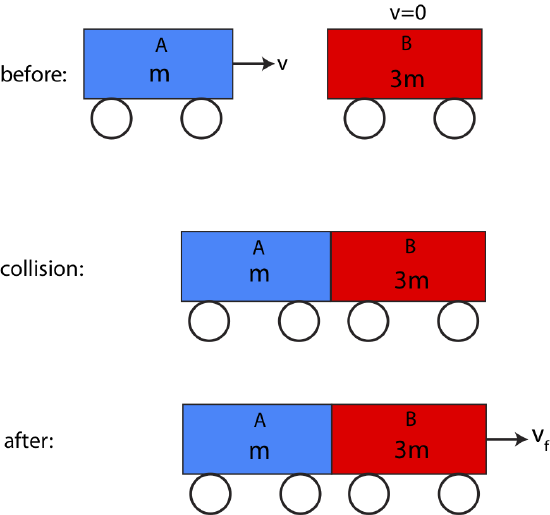
Assuming that there are no net external force acting on the system, we can figure out the final speed of the two stuck carts using momentum conservation. Let us use a momentum chart to guide us through this problem. The momentum chart can be filled out in the following order:
- initial momentum is given: pi,tot=pi,A+pi,B=mv+0. This fills out the first column.
- we set Δptot=0 since there are no external forces acting on the two carts, Jnet,ext=0.
- this implies that pf,tot=pi,tot=mv, filling in the last entry in the bottom row.
- the final momentum of cart A is pf,A=mvf, third entry in first row.
- cart B has the same speed as cart A but triple the momentum since it has triple the mass of cart A: pf,B=3mvf, third entry in second row.
- the individual values of ΔpA and ΔpB are calculated using Δp=pf−pi
Figure 7.2.8: Two-Body Inelastic Collision Momentum Chart
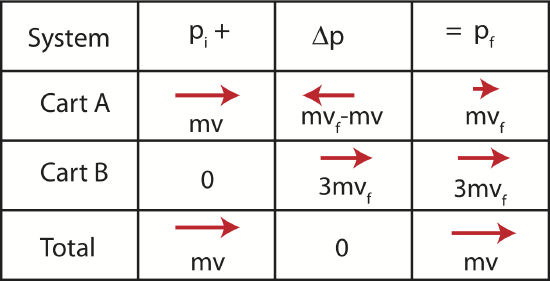
Once we have the momentum chart filled out we can solve for vf by other using the third column:
mvf+3mvf=mv
Resulting in:
vf=v4
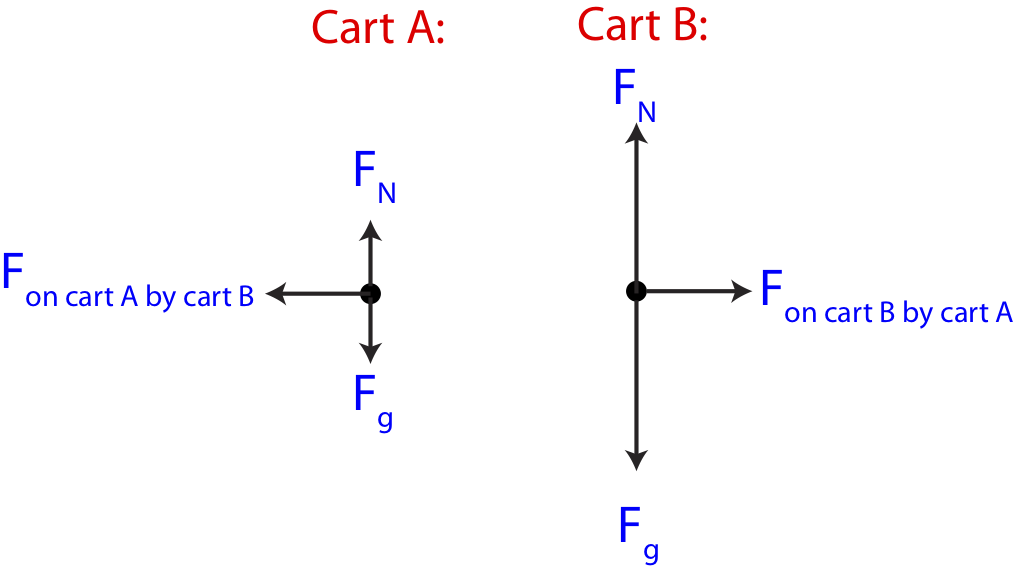
Or you can use the second column which states the the sum of the individual momentum changes must be equal to zero. The middle column is also consistent with Newton's 3rd law of motion since each cart experiences an equal and opposite force (and thus impulse) from the other cart. Below are force diagrams for each cart. The FBDs illustrate the 3rd law pair during this collision, since each cart is experiences a force by the other cart with equal magnitude by in the opposite direction. The force due to gravity is triple on cart B since it has triple the mass.
Figure 7.2.9: Two-Body Inelastic Collision Free-Body Diagrams
To show that the collision is inelastic, we need to compare the final and initial kinetic energies:
KEi,tot=KEi,A+KEi,B=12mv2+0
KEf,tot=KEf,A+KEf,B=12(m+3m)(v4)2=18mv2
ΔKE=KEf,tot+KEi,tot=18mv2−12mv2=−38mv2
If you think deeper about the examples we have see so far, one-body systems where momentum is not conserved and two-body where momentum is conversed, you might ask whether momentum conservation depends on a particular physical situation. This question goes back to the idea of defining a "system", which is an arbitrarily chosen particle or object or a collection of particles or objects. As in 7A an open system defined an object or a collection of objects which interacted with the environment allowing heat and/or work to enter and leave the system, thus, changing the energy of the system. But we could always redefine the system to include everything, i.e. the environment, in this case the system becomes closed, and energy of the system is always conserved.
Similarly, when calculating momentum conservation, we saw that an open system where momentum changed was one where there was a net force exerted by the environment on the system. As for energy analysis, we can always include the environment in the system, in which case it would become closed, with no external forces, and the only forces present being internal third-law pairs. In this case momentum would be always conserved.
This idea at first thought has rather mind-blowing consequences. Imagine that a rock falls on the ground and we analyzed the rock as an open system whose momentum changed when it fell and stopped on the ground, due to the force by the Earth on the rock. However, if we included the Earth in the system, there would be no longer external forces acting on the rock-Earth system, implying that the total momentum of this system has to be conserved. But this means that the collision of the rock "sticking" to the ground would make the Earth move, as in the scenario described in Figure 7.2.7, where the rock would represent the initially moving cart and the Earth is the stationary cart. This, of course, does not seem correct, we do not cause the Earth to move back and forth as we bounce balls and throw objects on the ground. Let us take a closer look at what is happening here. Applying Equation ??? (which helps us calculate the final speed due to a perfectly inelastic collision between two objects) to this scenario we need to replace the mass of the initially moving cart with the mass of the rock, mR, and the mass of the stationary cart becomes the mass of the Earth, mE. Solving for final velocity, we find that:
vf=mRmR+mEvi
Since the mass of the Earth is so much bigger than the mass of the rock, the ratio of masses in the above equation is basically zero, resulting in zero final velocity. So we saved the Earth from moving off into outer space by dropping a ball on the ground. The main message to get from this fun digression is that it is momentum which is conserved, and not velocity. So even though by including the Earth in the system we are seeing that the momentum of the Earth must changed due to this collision, its change of velocity is negligible since its mass so much larger than the mass of the object with which it interacts. This is directly related to the truck and bug example from the previous section, although the collision of the bug with the truck changes the momentum of the truck the same way the ball changes the momentum of the Earth by landing on the ground, the truck keeps on going with the same velocity as before the collision, since it is much heavier than the bug.
A good rule of thumb when choosing a system of objects which are interacting, is to include objects of similar size only. If you include everything and some of those objects are much more massive than others, you will not learn anything interesting about the massive objects since their motion will not change due to the interaction with the much smaller objects. Thus, it is more informative to leave them out, and define an open system where the massive object become a source of an external force on our selected system.
Example 7.2.2
Below is an illustration of a two balls colliding. Ball 1 on the left is initially moving to the right with speed, vo=4m/s while ball 2 is stationary. After the collision both balls are moving in opposite directions with some speeds as shown below. Ball 2 is twice the mass of ball 1. Assume no external forces are acting on the two-balls, and the collision is elastic.
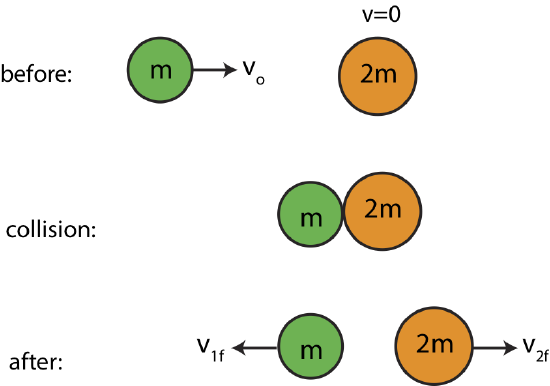
a) Calculate v1f and v2f.
b) Find the impulse on ball 1 by ball 2 and the impulse on ball 2 by ball 1, if the mass of ball 1 is 1.5 kg.
c) if in another scenario the two ball stick together instead, find the final velocity. Assume the initial conditions are the same. Is the collision elastic or inelastic? If inelastic, find the change in kinetic energy.
- Solution
-
a) Since there are no external forces acting on the two balls, the momentum of the two-ball system is conserved:
mvo=2mv2f−mv1f
The equation above has 2 unknowns, both final speeds. But we are also given that the collision is elastic, so kinetic energy is conserved:
KEi=KEf
KE1i+KE2i=KE1f+KE2f
12mv2o+0=12mv21f+12(2m)v22f
Now we have 2 equations with 2 unknowns, v1f and v2f. The initial velocity, vo is given but for now we will leave it as a known variable. The conservation of momentum and kinetic energy conservation equations can be simplified by canceling out common factors:
vo=2v2f−v1f
v2o=v21f+2v22f
The remaining steps in the solution are algebraic, let's use the first equation and plug into the second equation for vo:
(2v2f−v1f)2=v21f+2v22f
Squaring the left-hand side:
4v22f−4v2fv1f+v21f=v21f+2v22f
Canceling common terms on both sides and moving all the terms to the left-hand side we get:
2v22f−4v2fv1f=0
Factoring common terms:
2v2f(v2f−2v1f)=0
The above equation has two solutions, one states that v2f=0. This cannot be true in this case since you are told that both ball are moving after the collision. The other solution states that:
v2f=2v1f
So ball 2 is moving with twice the speed of ball one. To get a numerical result we need to relate the above result to initial speed vo:
vo=2v2f−v1f=4v1f−v1f=3v1f
Solving for v1f:
v1f=vo3=43m/s
Which means that:
v2f=2v1f=83m/s
b) The impulse on ball 1 by ball 2 is the change of momentum of ball 1:
Jon 1 by 2=Δp1=mv1f−mv0=1.5kg(−43−4)m/s=−8Ns
The impulse on ball 2 by ball 1 is the change of momentum of ball 2:
Jon 2 by 1=Δp2=2mv2f−0=2×1.5kg×83m/s=8Ns
You can see that the two impulses are equal in magnitude and opposite in direction, which is consistent with Newton's 3rd Law. It also shows that internal impulses cancel, so although the momentum of each individual object in a system consisting of multiple objects changes, the total momentum is conserved, since there is no net impulse acting on the system. All internal forces do not contribute to the total change of momentum of the entire system, in this case the two balls.
c) If the two ball stick together instead, then their final velocity has to be the same since they are moving together while attached. Let us call this velocity vf. Momentum is still conserved, since no external forces act on the two balls. Conservation of momentum for this case becomes:
mvo=mvf+2mvf=3vf
This results in:
v1f=vo3=43m/s
So both balls are moving to the right with speed of 4/3 m/s.
In this case since the balls stick together the collision is perfectly inelastic. The change in KE is:
ΔKE=KEf,tot−KEi,tot
ΔKE=12(m+2m)v2f−12mv2o
ΔKE=12(3m)(vo3)2−12mv2o=−13mv2o=−13(1.5kg)(4m/s)2=−8J
Two-Dimensional Collisions
We use the same impulse-momentum model to solve two-dimensional momentum conservation problems, except all the vectors are no longer described with just a plus or minus sign specifying the direction of motion, but now have two components for each spatial direction. Thus, although the physics is the same, the algebra become more cumbersome. The impulse-momentum model, →Jext=Δ→p, written by components in 2D is:
Jext,x=Δpx
Jext,y=Δpy
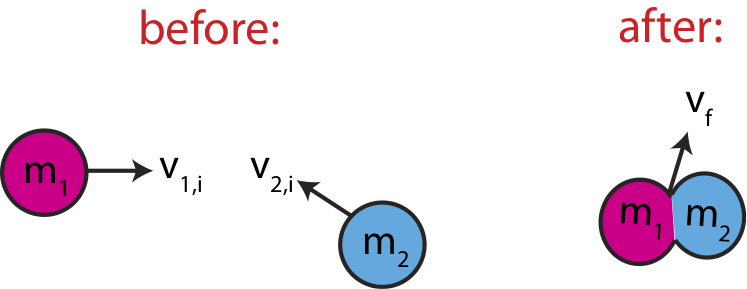
So one physical collision can be treated independently in each spatial direction, as if you are solving two separate 1D collisions. The only difference is the each component of given velocity describe the motion of the same object. Figure 7.2.10 is an example of a perfectly inelastic 2D collision, where two balls with different masses moving in two-dimensions collide and stick together. We assume no external forces are acting on the two-ball systems, thus the total momentum is conserved.
Figure 7.2.10: Two-Body Collision in 2D
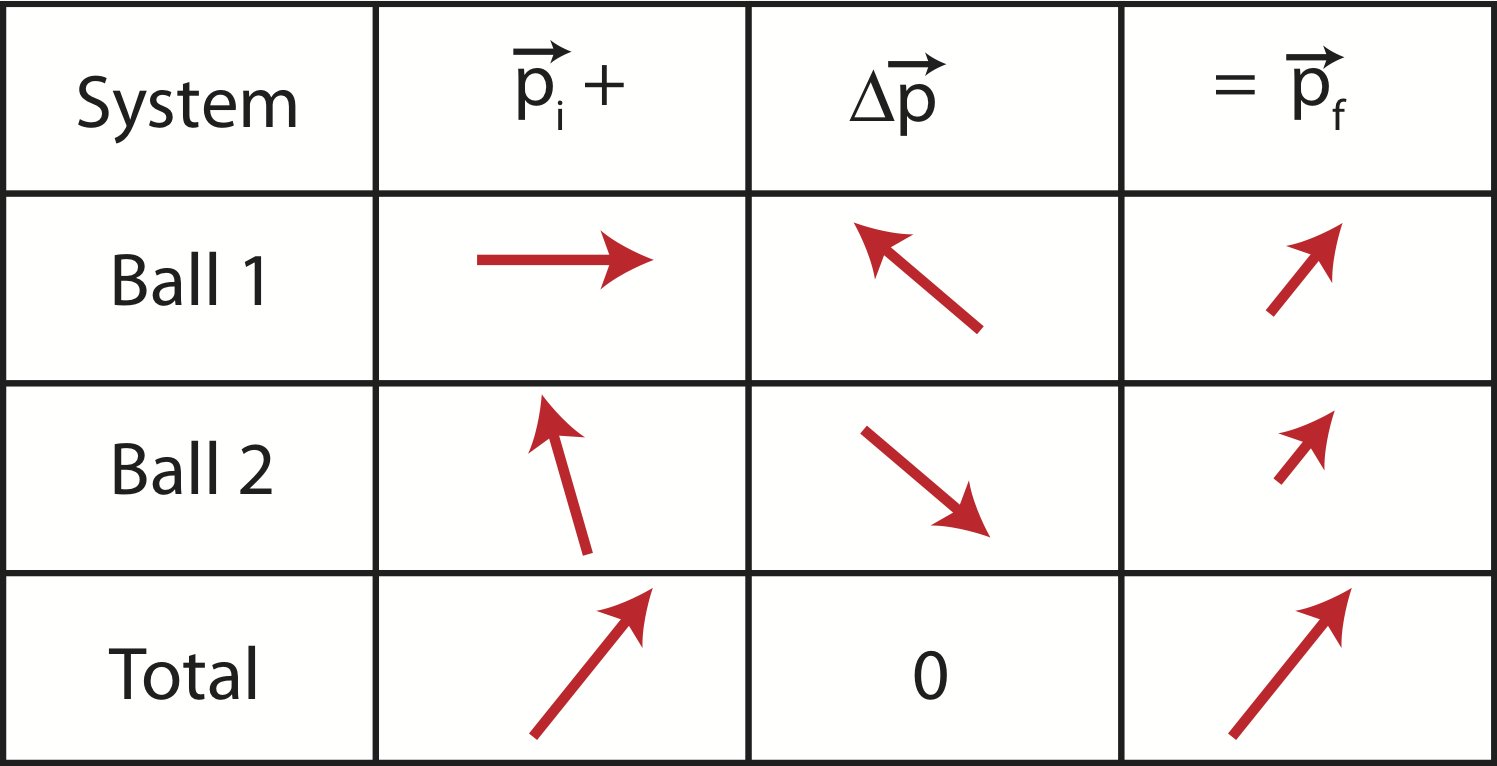
The momentum chart in Figure 7.2.11 illustrates an example of a momentum chart for the scenario. With the information given we cannot exactly draw a momentum chart, since we do not know the relative masses and velocities of the two objects.
But this momentum chart demonstrates the basic ideas of a 2D perfectly inelastic collision:
- the sum of initial momenta of each object equals to the total initial momentum.
- the total initial momentum is equal to the total final momentum, since the change in total momentum is zero when there is no net external impulse acting on the system in either spatial direction
- the individual final momenta for each object point in the same direction since they move together, but do not have the same magnitude when their masses are different.
- the individual changes of momenta for each object are equal in magnitude and opposite in direction.
Figure 7.2.11: Two-Body Collision in 2D
To solve for the final velocity of the two balls algebraically, we equate the initial and final total momentum, as we did for one-dimensional examples:
→pi,tot=→pf,tot
The total momentum is a vector sum of the individual momenta of each ball:
→pi,1+→pi,2=→pf,1+→pf,2
Alert
When doing momentum conservation problem it is really important to label your masses and velocities. Otherwise, it become very easy to loose track of variables and make mistakes. The masses should have subscripts specifying which objects you are referring to, such as m1 and m2. The velocities often have three labels, indicating the object, time period (before the collision or after the collision), and the spatial direction. For example, the final velocity of object 2 in the y-direction can be labeled as v2,f,y.
To sum the vectors we need to express each momentum by components. In the x-direction Figure 7.2.10 shows m1 moving to the right and m2 moving to the left initially. After the collision, both masses have a component of momentum in the positive x-direction. Thus, Equation ??? in the x-direction is:
m1vi,1+m2vi,2,x=(m1+m2)vf,x
Note, the subscripts in Equation ???: the initial velocity of m1 does not have an "x" subscript since all of its velocity is in the x-direction so there is no reason to keep the x-component notation. When we were working with 1D examples at the start of this section, we didn't carry the notation of direction along which the system was moving since it was understood that motion was happening in that one direction. The only distinction which was necessary is to specify right/left or up/down with a plus or minus sign. Since →vi,2 has both x- and y-components we need to specify that the momentum conservation equation in the x-direction includes the x-component of this velocity, which is negative since m2 is moving in the northwest direction (negative x- and positive y-). For the final momentum, the velocity is the same for both masses, so there is no meaning to the subscripts "1" and "2", thus it is left simply as →vf with the x-component included in this equation for the x-components.
In the y-direction Equation ??? becomes:
m2vi,2,y=(m1+m2)vf,y
If your goal for to calculate the final velocity, assuming that you were given values of initial velocity and masses, you would solve for each component of the final velocity using Equations ??? and ???:
vf,x=m1vi,1+m2vi,2,xm1+m2
vf,y=m2vi,2,ym1+m2
After calculating the components you can use Pythagorean theorem and trigonometry to solve for the speed and the angle of the final velocity.
To figure out the change in kinetic energy the concepts are the same as they were in 1D, since it is only the speeds of the objects that matter, not the direction in which they travel. The change is kinetic energy for this example is:
ΔKE=KEf,tot−KEi,tot=[12(m1+m2)v2f]−[12m1v2i,1+12m2v2i,2]
In this particular example, as in appears in Figure 7.2.10 the combined mass system is moving in the northeast direction. However, they can be other scenarios where the masses move in a different direction after the collision. The final velocity depends on the initial velocities and masses. Let us think of an extreme example where both objects move with the same speed but ball 1 is much heavier than ball 2. In this case the momentum of ball 1 will be much greater and the initial momentum of ball 2 will have very little effect, so the final velocity of the two objects will be in the east direction. Think back to our truck and bug example. If m1 represented a moving truck and m2 is a bug that landed on the truck and got stuck to its windshield, the truck would continue moving with its initial momentum.
As another example, let us examine a situation where both masses are moving north (in the positive y-direction) after the collision. If both have the same initial speed, and ball 2 is moving at a angle of 60∘ from the negative x-axis, let us figure out their ratio of their masses in order for this to happen. Applying Equation ??? to this scenario we get:
m1vi−m2vicos60∘=0
The right-hand side of the equation is zero since the final velocity does not have an x-component in this example, and we drop the "1" and "2" subscripts from the initial velocity since the speed is the same for both balls. Solving for the ratio of the masses we get:
m1m2=cos60∘=12
So ball 2 has to have weight double of ball 1, for them to stick and travel north. This result is independent of the initial speed. To find the final speed we need to set up the equation for the y-direction. Equation ??? for this situation becomes:
m2visin60∘=(m1+m2)vf
So the final speed depends on the initial speed:
vf=m2m1+m2visin60∘=23visin60∘
This result shows that the final speed will depend on the initial speed of the two masses.
Example 7.2.3
An astronaut is drifting in space away from her spaceship with speed of 3 m/s and an angle of 30∘ from the positive x-axis as shown below. She needs to get back to her spaceship in order to feed her dog, Cupcake. Using her physics knowledge, she takes off her heavy 20 kg backpack and throws it. After the throw the astronaut is traveling toward the spaceship at an angle of 50∘ below the positive x-axis, and the backpack is moving straight in the y-direction. The astronaut weighs 70 kg. Assume no external forces are present.
a) Find the speed of the backpack after the astronaut threw it and the speed of the astronaut as she approaches the spaceship, as seen by Cupcake.
b) Find the impulse with which the astronaut threw the backpack. Express your answer in terms of magnitude and direction.
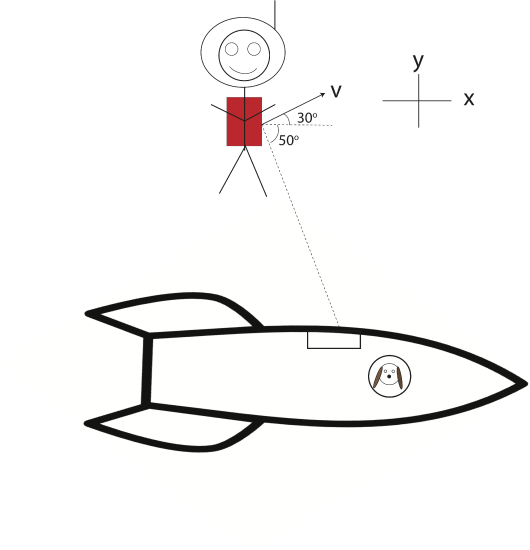
- Solution
-
a) We want to define the system to include the astronaut and the backpack, since they initially travel together but after the interaction (the throw), they move with different velocities. The total momentum of the system is conserved since no external forces act on the astronaut-backpack system. This means that:
Δ→ptot=0
→pi,tot=→pf,tot
The initial momentum is just the combined mass of the astronaut and backpack, since they are attached, multiplied by the initial velocity:
→pi,tot=(mA+mB)→vi
where mA is the mass of the astronaut, and mB is the mass of the backpack. By component the initial momentum is written as:
pi,x=(mA+mB)vicos30∘
pi,y=(mA+mB)visin30∘
Both components are positive since the initial velocity is in the northeast direction.The total final momentum includes the individual momentum of the astronaut and backpack since they are no longer attached:
→pf,tot=→pf,A+→pf,B=mA→vf,A+mB→vf,B
The backpack's velocity only has a positive y-component after the throw. Simplifying the above equation and using the information about the direction of astronaut's motion after the throw we get:
pf,tot,x=mAvf,Acos50∘+0
pf,tot,y=−mAvf,Asin50∘+mBvf,B
Equating initial and final momentum in each direction we get:
(mA+mB)vicos30∘=mAvf,Acos50∘
(mA+mB)visin30∘=−mAvf,Asin50∘+mBvf,B
First we use the equation for the x-direction to calculate the final speed of the astronaut, since the equation in the y-direction has two unknowns:
vf,A=(mA+mB)vicos30∘mAcos50∘=(90kg)(3m/s)cos30∘(70kg)cos50∘=5.20m/s
Next we use the equation for the y-direction to calculate the final speed of the backpack:
vf,B=(mA+mB)visin30∘+mAvf,Asin50∘mB=(90kg)(3m/s)sin30∘+(70kg)(5.20m/s)sin50∘20kg=20.7m/s
b) The impulse on the backpack by the astronaut is equal to the change in the backpack's momentum:
→Jon B by A=Δ→pB=→pf,B−→pi,B
Using the results from a) and solving by component:
Jon B by A,x=pf,x,B−pi,x,B=0−mBvi,x,B=−(20kg)(3m/s)cos30∘=−52kgm/s
Jon B by A,y=pf,y,B−pi,y,B=mBvf,y,B−mBvi,y,B=(20kg)(20.7m/s)−(20kg)(3m/s)sin30∘=384kgm/s
Combining results the magnitude of the impulse is:
|→Jon B by A|=√522+3842=387.5kgm/s
And the angle is the 2nd quadrant (northwest):
θ=arctan(38452)=82.3∘
Contributors
Authors of Phys7A (UC Davis Physics Department)


