7.1: Linear Momentum

Overview of Model

In the previous chapter we discussed how the forces acting on an object effect the motion of that object. In this chapter some of these concepts will lead us directly to a new conservation law: the conservation of momentum. The goal of the remaining chapters in this book is to understand the effects of forces on motion in greater detail, and we begin to do this in this chapter through a discussion of momentum and transfers of momentum.

We introduce two new concepts: momentum and impulse. Although these terms are new, it is often helpful to make connections to things we already know. So we start the discussion of momentum and impulse by pointing out their similarities to energy and work. When work is done on a system it changes the energy of the physical system. When there is no work that is done on the system, energy is conserved. Similarly, a net impulse done on a defined system changes the momentum of a system.  When the net impulse acting on the system is zero, momentum is conserved. 

Effect of Force

We have learned from Physics 7A that objects experience changes in energy when other objects exert forces on them and do work on them. We recall that the amount of energy change caused by a force is the integral of the force over a displacement or path of the object. This integral is called the work done on a system. The general algebraic expression for work done along a path \(s\) from point A to B was defined in Section 2.3 is given by:

\[ W \equiv \int \limits_A^B \overrightarrow F_{net} \cdot \overrightarrow {ds}=\Delta E= E_f-E_i\label{work}\]

The dot product, \(\overrightarrow F_{net} \cdot \overrightarrow {ds}\), in the equation above means that only the component of the force parallel to the displacement contributes to work. In other words, the parallel component of force integrated over the path of the motion is the work. This work equals the amount of energy transferred to the system due to the application of the force by an object outside the system. It is always important to stress the the change in energy on the right-side of Equation \ref{work} is the change of energy of some defined system, while the work on the left-side of the equation refers to external work done on the system by objects outside the system.

Equation \ref{work} tells us that the path over which the force will act will determine how the energy of the system will change. There is another factor that will determine how the system will change, the time over which the force will act. We know that the resulting motion of a toy car will be different depending if you briefly give it a push or keep pushing it for a prolonged time before letting it go. In the latter case, the car will move for a longer distance, after you stop pushing it, until it reaches an obstacle or friction will cause it to stop. Thus, we want to introduce a new concept that depends on force and the time over which the force acts, known as the impulse of the force. If the force is not constant during some range of time, then instead of simply multiplying force and time, we would have to integrate it. Impulse which is a vector (force) times a scalar (time), is a vector. We represent impulse with the symbol \(\vec J\):

\[\vec J \equiv \int\limits_{t_i} ^{t_f} \vec Fdt \]

If the force is constant over some time, \(\Delta t=t_f-t_i\), then the impulse equation simplifies to, \(\vec J=\vec F \Delta t\). Let us now use Newton's second law described in Section 6.2 to help us determine how impulse effects the motion of a system:

\[\begin{array}{l} \vec J && = && \int\limits_{t_i} ^{t_f} \vec Fdt \\ && = && \int\limits_{t_i} ^{t_f} (m\vec a) dt \\ && = && \int\limits _{t_i} ^{t_f} \Big(m\frac{d\vec v}{dt}\Big) dt \\ && = && m\Delta\vec v\Big |_{t_i}^{t_f} \\ &&= && m\vec v_f-m\vec v_i \end{array} \label{Jp}\]

We arrive at a definition of a vector quantity we call momentum, \(\vec p\):

\[\vec p\equiv m\vec v\]

From Equation \ref{Jp}, this results in a relationship between impulse and momentum, known as the impulse-momentum model:

\[\vec J =\Delta\vec p\label{IM}\]

To summarize the impulse-momentum model in words: impulse, \(\vec J\), is a vector quantity, defined as an external force acting on a system over some time period, which causes a change in a vector property of a system, specifically, a change in momentum, \(\Delta \vec p\). This is analogous to the result in Equation \ref{work}: work, \(W\),  is a scalar quantity, defined as an external force acting on a system over some path, which causes a change in a scalar property of a system, specifically, a change in energy, \(\Delta E\). Although, both work and impulse give us a quantity which is the effect of forces, there are some fundamental differences. Work is a scalar, while impulse is a vector. Also, to find work you need to know the specific path over which the system moves, while only the time over which the force acts determine impulse.

The momentum introduced here, \(\vec p\), is linear momentum, the word "linear" implies that the motion is described by displacement (distance changing) with time. In the following section we will introduce angular momentum, which describes motion in terms of a change of an angle with time. In this section, we will mostly refer to \(\vec p\) as just "momentum", for simplicity.  In general, we will refer to this type of momentum as linear momentum when we want to distinguish it from angular momentum.

Note on units: force has SI units of Newtons, \(\textrm{N}\). Impulse must therefore have units of Newton seconds, \(\textrm{N}\cdot\textrm{s}\). Momentum, the product of mass and velocity, must have SI units of kilogram meter per second, \(\textrm{kg}\cdot\textrm{m/s}\). Since these two quantities are equated, these units must be equivalent, as you can show using the relationship that force equals to mass times accelation: \(\textrm{N}=\textrm{kg}\cdot\textrm{m}/\textrm{s}^2\).

Until we consider rotation of objects in the next mode, when we talk about angular momentum, we will consider phenomena in which extended objects act only like point particles. A useful concept that will become much more meaningful when we consider rotation, is center of mass. Right now we can simply consider that any extended object acts like a single particle whose mass is equal to the mass of the object, located at the special point, the center of mass.

Momentum of a System with Multiple Particles

It is often useful to evaluate interaction between multiple particles in terms of momentum. Specifically, the impulse-momentum model will help us understand the motion of particles after they exert forces on each other, such as two billiard balls colliding. The momentum of a single object is simply the product of its mass and velocity. Suppose we define a physical system that contains several particles which may have different masses and move with different velocities. The total linear momentum of this physical system consisting of \(N\) particles is the vector sum of the individual linear momenta:

\[\vec p_{\textrm{system}} = \vec p_1+\vec p_2+\vec p_3+...+\vec p_N=\sum_{i=1}^{N} \vec p_i\label{psum}\]

If the particles in our system interact with each other, they exert forces on each other, and there will be an impulse associated with each of these forces. Figure 7.1.1 below depicts two carts that come in contact with each other, thus exert a force on each other. Newton’s 3rd law, described in Section 6.2, tells us that the force that cart A exerts on cart B is equal in magnitude and opposite in direction to the force that cart B exerts on cart A, as shown in the picture below.

Figure 7.1.1: A system of Two Objects

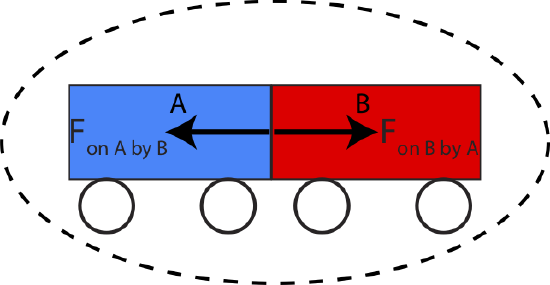
Since impulse is the force integrated over time during which the carts are in contact, the impulses on A and on B will also be equal and opposite:

\[\vec J_{\textrm{on A by B}}=-\vec J_{\textrm{on B by A}}\]

The impulse on each separate object within the system equals to the change in that object's momentum:

\[\vec J_{\textrm{on A by B}}=\Delta\vec p_A\nonumber\]

\[\vec J_{\textrm{on B by A}}=\Delta\vec p_B\]

Using Equation \ref{psum} for the total momentum of a system and the two equations above, we then find that the total change of momentum of a system consisting of two objects A and B is:

\[\Delta\vec p_{\textrm{system}} = \Delta\vec p_A+\Delta\vec p_B=\vec J_{\textrm{on A by B}}+\vec J_{\textrm{on B by A}}=0\]

Generalizing the above argument to interactions between any of the particles within the system, we see that if the momentum of one particle changes a certain amount, another particle’s momentum changes the same amount in the opposite direction. Thus, when we sum over all the momenta of the system, the total momentum of the system does not change in response to interactions among the particles within the system.

However, if the particles of our define system interact with particles (objects) outside the system, then the total momentum of the system might change. Figure 7.1.2 below shows a force that acts on the two-cart system. This force is from another system, for example, as a third cart or a hand pushing the two carts. As argued above the internal forces between the two carts do not change the total momentum of the system. However, the external force labeled ext (for external) does change the momentum of the system based on Equation \ref{IM}. There is no other force present to cancel the force on system 1 by system 2. 

Figure 7.1.2: A system of Two Objects with External Force

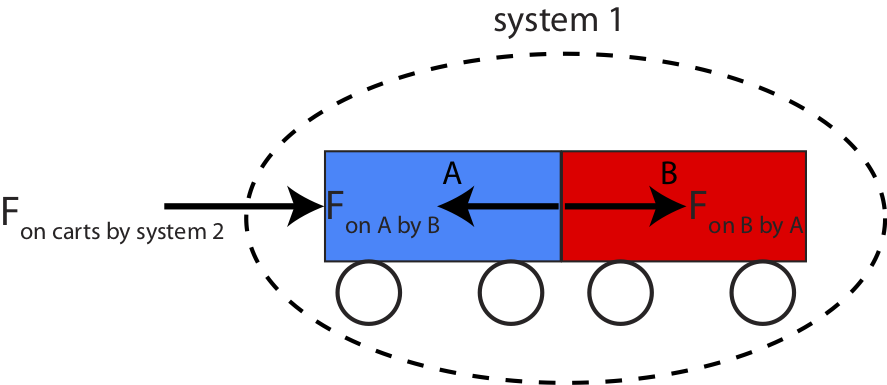
Also, it is important to note that when we derived Equation \ref{Jp} using Newton's 2nd Law, it is the net force acting on the system which determines its acceleration, so the impulse which changes momentum is the impulse due to the net force acting on the system.

Conservation of Momentum 

To summarize the above discussion, for a system of particles or objects it is useful to write the impulse-momentum model in a way that emphasizes the external net interaction:

\[\textrm{Net external impulse}=\vec J_{net,ext} = \int\limits_{t_i}^{t_f} \sum \vec F_{ext} dt= \Delta\vec p_{\textrm{system}}\]

We will often drop the "net" and "ext" subscripts, for simplicity, but please always keep in that that this is what is implied in the the impulse-momentum model. A system acted on by external forces undergoes a change in total linear momentum equal to the net impulse (total impulse) of the external forces. We can rephrase the relationship stated above as a conservation principle for the total linear momentum of a system of particles:

Conservation of Momentum 

If the net external impulse acting on a system is zero, then there is no change in the total linear momentum of that system. Otherwise, the change in momentum is equal to the net external impulse.

This statement is an expression of conservation of linear momentum. The total linear momentum of a system of objects remains constant as long as there is no net impulse due to forces that arise from interactions with objects outside the system. It does not matter that the objects of the system interact with each other and exert impulses on each other. These internal impulses cause changes in the individual momenta of the objects, but not the sum or total momentum of the system of objects.

In the light of this discussion, it is useful to categorize systems as either closed or open:

1. Closed system - a closed system does not interact with its environment so there is no net external impulse acting on it. The total momentum of a closed system is conserved. That is, the total momentum of the system remains constant. A closed system can consist of one or multiple objects.
2. Open system - an open system interacts with its environment, so that it can exchange both energy and momentum with the environment. The change in the total momentum of an open system is equal to the net impulse from the environment outside the system. An open system can consist of one or multiple objects.