9.5: Hydrogen Like Atoms

Hydrogen Atom Energy Levels

The next system we study is a very useful one, an electron bound to an orbit around a nucleus. The simplest case of such a system is a hydrogen atom which has one electron which orbits its atomic nucleus. In this situation, the electron has both kinetic energy and potential energy described by the electrostatic potential which we will study in detail in Chapter 11. Also, the electron orbits the nucleus in three-dimensional space, so the wave functions, described "standing waves" imposed by the electrostatic potential can no longer be described by simple one dimensional waves with alternative nodes and anti-nodes. Instead, these become much more complex, as depicted by atomic orbitals in the figure below.

Figure 9.5.1: Atomic Orbitals

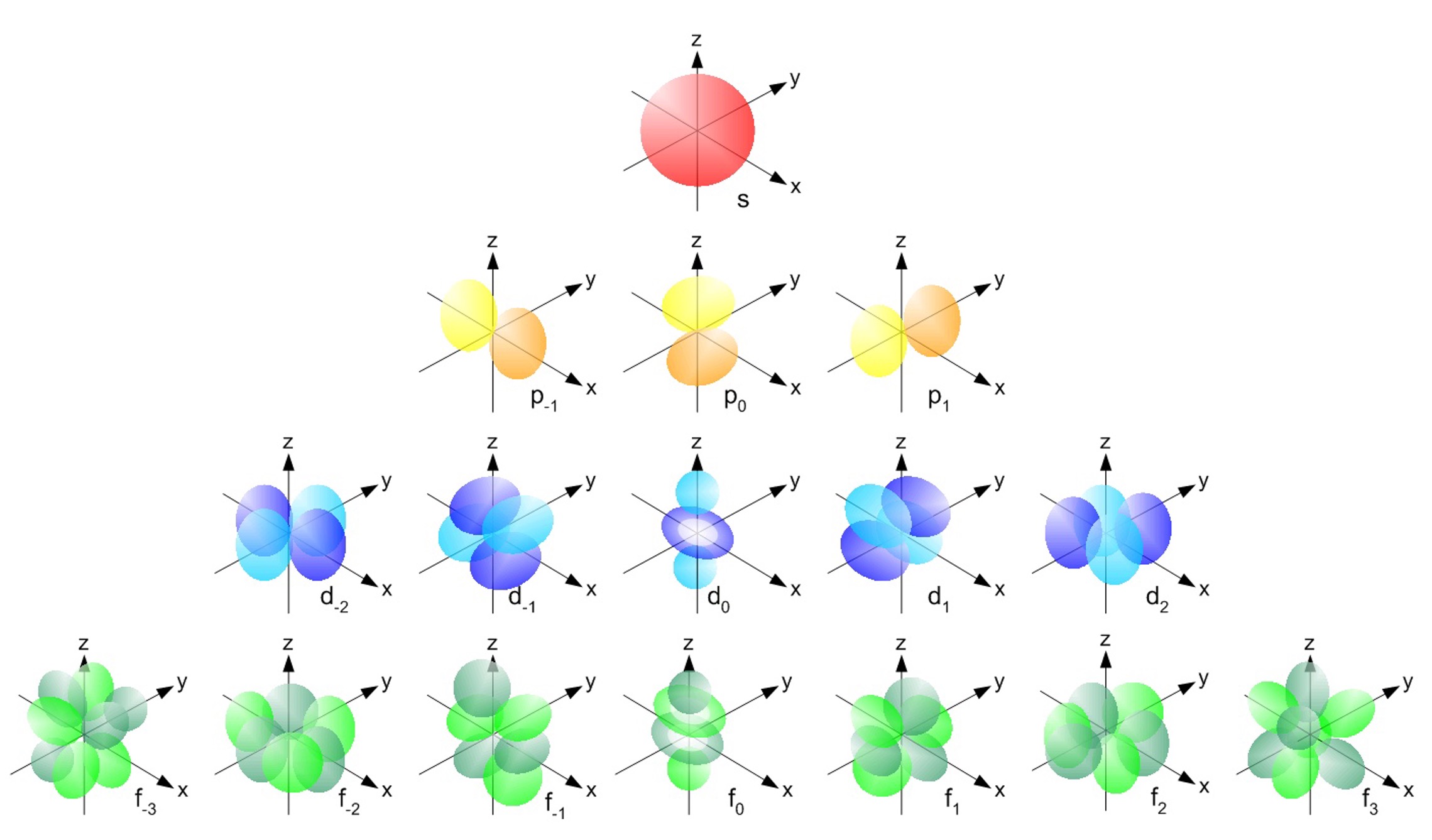
The details behind these orbitals are outside the scope of this class. However, we can still appreciate what they represent. Like for the one-dimensional case, the orbitals represent the probability of finding the electron around the nucleus and correspond to a specific frequency. The colored regions represent anti-nodes, locations where the probability is highest, while the spaces in between are nodes where probability goes to zero.

Quantum mechanics predicts the following expression for the energy levels of a hydrogen-like atom, when both the kinetic energy and the electrostatic potential are incorportated into the total energy:

\[E_n=-\dfrac{13.6 \text{eV}}{n^2}Z^2;~~~n=1,2,3,...,\infty\]

where \(Z\) is the atomic number, or the number of protons. For a hydrogen atom whose atomic numbers is one, (Z=1\), the lowest energy state is \(E_o=-13.6 \text{eV}\). All of these are one-electron atoms, so atoms with a higher atomic number than hydrogen will be ionized. Helium, \(Z=1\), will have one electron removed, \(He^{+}\), lithium, \(Z=2\), will have two electrons removed \(Li^{2+}\), and so on. The figure below shows the energy spectrum for hydrogen, displaying the first five energy levels.

Figure 9.5.2: Hydrogen Energy Levels

The energy levels for hydrogen-like atoms get closer together as energy increasing, since the quantized energy is proportional to \(1/n^2\). We've established earlier that we could arbitrarily choose "zero" energy to be any amount of energy. Above, we have chosen zero to refer to the energy of an unbound electron, and each energy level shown has a negative energy in comparison. The ground state energy level (\(n = 1\)) is the most bound state. Adding (allowed) energy to the electron will increase \(n\), making its total energy less negative, or even zero (as \(n\) approaches infinity). At this point, the electron will be unbound and free, and then will be allowed to have any (positive) value of energy. 

Absorption and Emission Spectra

As before electrons can move up to a higher energy level by absorbing photons, and then fall back down to lower energy levels by emitting photons. Analyzing the frequencies or wavelengths of light absorbed and emitted by different elements is a powerful scientific method of determining the atomic composition of substances, such as distant start in the sky.  

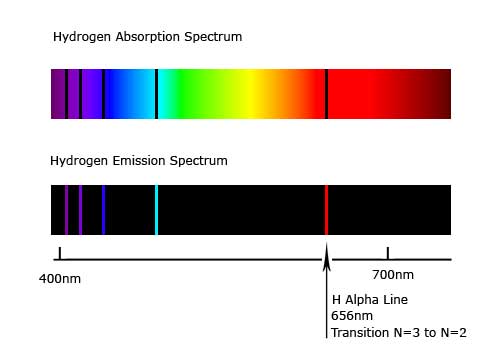
When you shine light composed of multiple frequencies on an element, the quantized energy levels will only allow certain frequencies to be absorbed. All other frequencies will be pass through the atoms and can be detected. The absorption spectrum of a particular atom will show black lines (absence of light) which correspond to the frequencies of light which were absorbed. The figure below shows the absorption spectrum of hydrogen in the visible range. The red side of the spectrum corresponds to longer wavelengths, thus lower energies, while the blue side shows higher energy transitions. We can see that the levels get closer together as energy increases.

Likewise, the emission spectrum of hydrogen shown above, depicts wavelengths of light which are emitted when electrons at higher energy levels fall back to lower ones. You can see in the figure, that the same wavelengths that were absorbed by the electron gained energy were emitted when the electron lost energy.  If we heat up a tube of hydrogen, many of the electrons are excited out of their ground states and into higher energy states. As these electrons fall to lower energy levels, they emit photons whose frequencies correspond to the energy transitions. The emission spectrum of hydrogen can be directly calculated from the energy level transitions. The emission spectrum for other elements are more complicated to calculate because other elements have multiple electrons that interact with each other and with the nucleus.

Figure 9.5.2: Absorption and Emission Spectra

Because the atoms of each element have different energy transitions, the emission spectrum and absorption spectrum of each element is unique. This uniqueness is exploited in spectroscopy, where unknown atoms and molecules can by identified by the energies (frequencies) of photons that they emit or absorb.

Burning samples of chemicals is another way to excite electrons. We might expect to see some correlation between the emission spectrum and the color of chemical fires. In practice, we do indeed see this similarity. The color of chemical fires is due to the emitted photons. To take a specific example, burning sodium produces a bright yellow flame. We can understand this by studying the emission spectrum of sodium, which includes many photons but only two in the visible range. Both of the visible photons have wavelengths of about 590 nm which corresponds to yellow light. The color of the flame is yellow because of these yellow spectral lines. You may be familiar with sodium vapor street lamps, which operate on the principle of exciting sodium atoms, and emit yellow light!

Example \(\PageIndex{1}\)

Light including the infrared, visible, and ultraviolet hits a bunch of hydrogen atoms at nearly 0K. The light is detected after hitting the atoms.

a) How is the detected light different from the incoming one?

b) Considering only transitions that allow the electron to remain bound, determine the longest possible wavelength absorbed.

c) Considering only transitions that allow the electron to remain bound, determine the shortest possible wavelength that could be absorbed.

d) Is the photon wavelength required to make a transition for \(He^{+}\) longer, shorter, or the same compared for a photon absorbed for the same transition in a hydrogen atom? If different, by how much?

Solution

a) The light incident on the hydrogen atoms includes a full range of frequencies, and thus a full range of energies. When the light hits the hydrogen atoms, some of the photons with exactly the right energy will excite the electrons into higher energy levels. The other photons will pass through unimpeded. Thus, the light reaching the detector will no longer contain the full range of frequencies; it will not contain frequencies corresponding to transition energies in the hydrogen atom. In the case of hydrogen most of the light at high frequencies is absorbed by ionizing atoms. 

b) Longer wavelengths of light have lower frequencies. Photons with lower frequencies have lower energies. To find the longest wavelength absorbed we must find the smallest amount of energy absorbed. Since the atoms are close to absolute zero, we can assume that the electrons are initially in the ground state. The lowest energy transition is from the ground state (\(n=1\)) to the \(n=2\) level. To make this transition, it must absorb a specific amount of energy:

\[E_{\text{photon}}=\dfrac{hc}{\lambda}=\Delta E=E_2-E_1=-13.6eV\left(\dfrac{1}{2^2}-\dfrac{1}{1^2}\right)=10.2 \text{eV}\nonumber\]

Solving for wavelength:

\[\lambda=\dfrac{hc}{\Delta E}=\dfrac{1240 \text{eV}\cdot \text{nm}}{10.2 \text{eV}}=122 nm\nonumber\]

c) Shorter wavelengths of light correspond to higher frequencies and higher energies. The highest energy transition available is from \(n = 1\) to a very large \(n\), just before the electron is freed from the atom. The initial state is the ground state, with energy −13.6 eV, and the final state approaches 0 eV. For the electron to gain 13.6 eV of energy, it must absorb a photon with that much energy. Mathematically,

\[\Delta E = E_{\infty}-E_1=-13.6\text{eV}\left(\dfrac{1}{\infty}-\dfrac{1}{1^2}\right)=13.6 \text{eV}\nonumber\]

Solving for wavelength:

\[\lambda=\dfrac{hc}{\Delta E}=\dfrac{1240 \text{eV}\cdot\text{nm}}{13.6 eV}=91.2 \text{nm}\nonumber\]

d) For ionized helium the energy levels are four times greater than that of hydrogen since Z=2. Thus, for a transition between any two levels the photon needs to have four times the energy for helium compared to hydrogen. Since wavelength is inversely proportional to energy, the wavelength needs to be four times shorter.