9.4: The Infinite Potential Well
- Page ID
- 66059
In almost all beginner quantum mechanics classes, the first type of potential which is studied is the "particle in a box". This potential describes a particle which is confined to a physical location, such as a wave confined to the length of a string attached at two ends. Even though the potential is not very realistic, it is the simplest to calculate and still provides a very intuitive understanding of the workings of quantum mechanics. We will describe a particle which is trapped in a one-dimensional box of fixed size but is completely free within the box. To keep the particle trapped in the same region regardless of the amount of energy it has, we require that the potential energy is infinite outside this region, hence the name infinite potential well. We then set "zero" potential energy to be the energy inside the box. The graph below shows the potential energy of a well with length \(L\).
Figure 9.4.1: The Infinite Potential Well
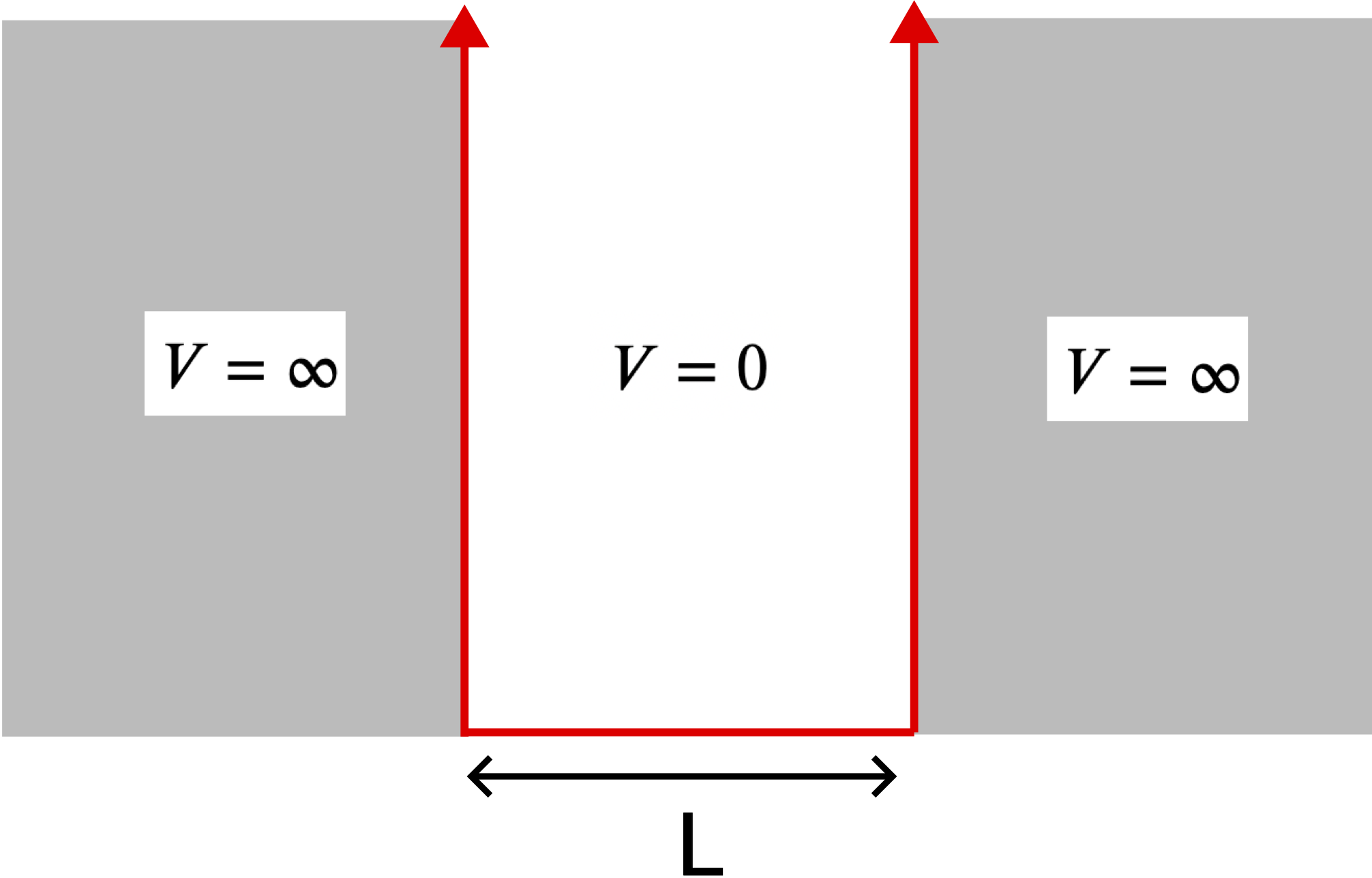
The infinite well seems to be the least useful of the situations we will study, as very few physical situations are similar to the infinite well. We introduce this system because it has the simplest potential available, zero inside the box and infinite outside of it. Also, since there is zero potential energy inside the box, the total energy of the particle is equivalent to the kinetic energy of the particle. If the particle gains total energy, we know it must have gained kinetic energy.
A classical particle trapped in box can have any value of kinetic energy as energy is added to the box. However, we now need to consider the wave nature of our quantum particle. Recall that on a string with two fixed ends, the generated wave had to have zero displacement at the two ends since that part of the string could not vibrate. Analogously, the particle cannot be present at the boundaries of the box, since it would have to have infinite energy. Thus, the displacement of the matter wave, known as the wave function, \(\Psi(x,t)\), must be zero at the boundaries of the box.
We can apply exactly what we know about standing waves in one-dimension to the particle in a box model, since the two-fixed ends are perfectly analogous to the two walls of the box. We learned in Section 8.8 on standing waves that the allowed wavelengths for a system with two fixed ends are:
\[\lambda_n=\dfrac{2L}{n};~n=1,2,3,...\infty\label{ln}\]
The infinite walls of the potential well assure that the particle cannot exist at the boundary between the wall and the outside. Therefore, the same quantized wavelengths apply to the one-dimensional particle in a box, where \(L\) represents the length of the box. Using the de Broglie wavelength equation from Section 9.3 we conclude that if the allowed wavelengths are quantized, so must be the momentum of the particle:
\[\lambda_n=\dfrac{h}{p_n}\label{Broglie}\]
The total energy of the particle is its kinetic energy plus the potential. Given that the potential energy inside the well is zero, the total energy of the particle is:
\[E_n=KE+PE=KE=\dfrac{1}{2}mv_n^2\]
where \(m\) is the mass of the particle and \(v_n\) is its speed which must be quantized. The kinetic energy can be rewritten in terms of the particle momentum using \(p=mv\). Thus, the above equation becomes:
\[E_n=\dfrac{p_n^2}{2m}\]
Finally, using equations \ref{ln} and \ref{Broglie} and plugging into the equation above we get the following expression for the quantization of energy for a particle in a one-dimensional infinite box:
\[E_n=\dfrac{h^2}{2m\lambda_n^2}=\dfrac{h^2}{8mL^2};~n^2~n=1,2,3,...\infty\]
The minimum amount of energy the particle can have is when n=1: \(E_1 = \frac{h^2}{8 m L^2}\). The potential energy is zero inside the box, so the particle always has some kinetic energy. For a quantum particle in a box it is impossible to sit at rest.
The figure below shows the energy spectrum for a particle trapped in a one-dimensional infinite well potential. In addition the wave function corresponding to each energy level is depicted. The wave functions are identical to the standing waves generated on a string with two fixed ends. However, since we are are discussing particles, the wave function has a different meaning. Specially, the wave function is related probability of finding the particle in a specific location in space. Since probabilities cannot be negative, it is the wave function squared, \(|\Psi(x,t)|^2\), which gives us the probability directly.
Figure 9.4.2: The Infinite Potential Well Energy Levels
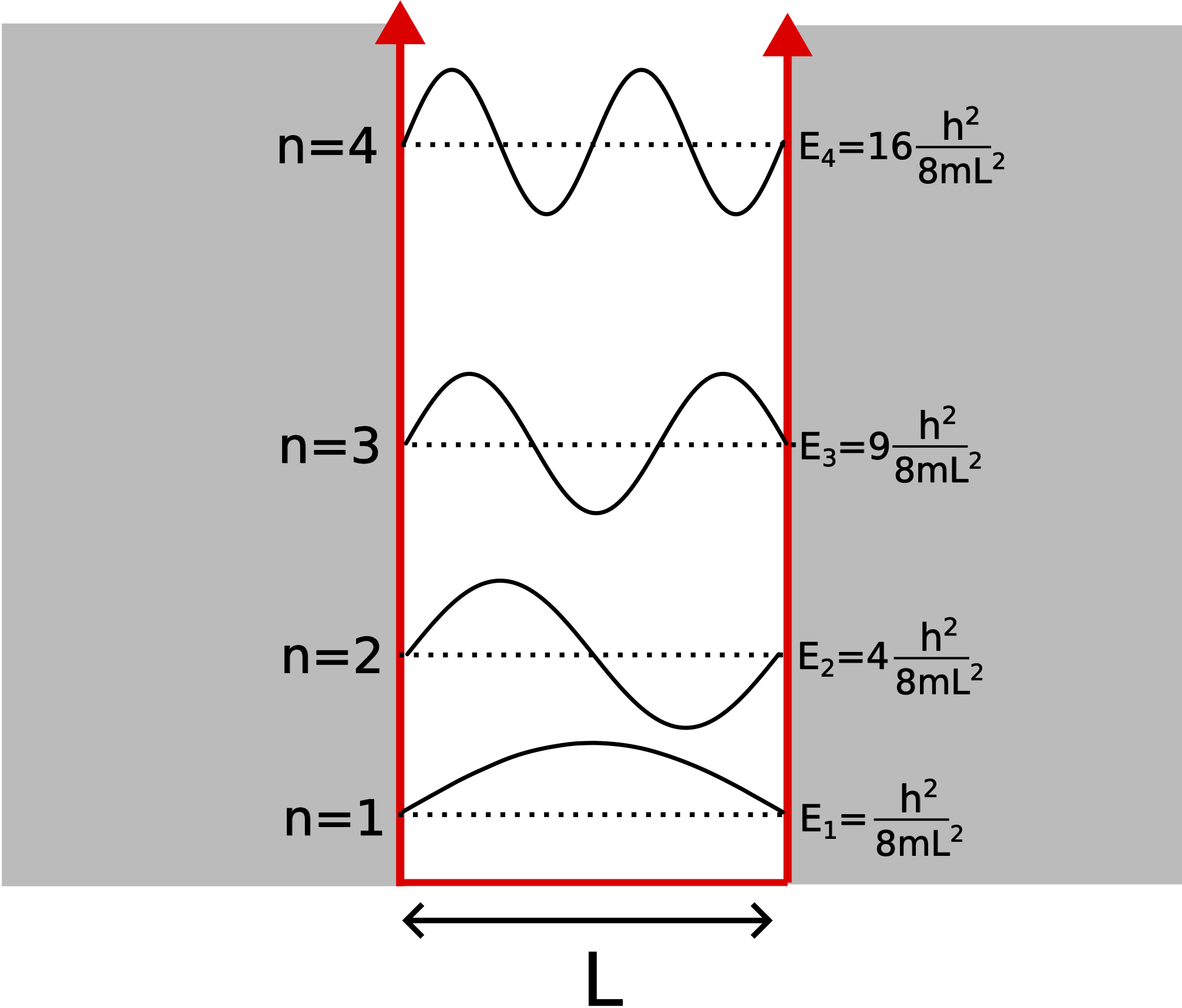
Looking at the wave functions above, the particle has zero probability of being at the boundaries of the wall (nodes) for all energy levels. For the first energy level, the particle has maximum probability of being at the center of the box (antinode). For the second energy level, there are two locations of maximum probability. Of course, the sum of these probabilities cannot exceed one.
For the infinite well potential, the energy levels are proportional to \(n^2\). This means the gaps between lower energy levels are smaller than those between higher energy levels, as depicted above. So as the particle gains energy, it takes more energy to transition to a higher level. Also, the energy gap between consecutive levels is smaller if \(L\) is bigger. So if the potential well becomes wider, it becomes easier to transition between levels, eventually reaching the classical (continuous energy) limit as \(L\) gets very larger or if the particle is very massive. This is why you cannot witness quantum behavior of a macroscopic particle trapped ina macroscopic box. This model applies to atomic particles, such as electron, in a box whose length is on the order of the size of an atom.
An electron trapped in a small box with infinite boundaries is initially in its ground state. It then absorbs a photon which excites it to the first excited state. The wavelength of this photon in \(\lambda_o\). Then it absorbs another photon which excites it from the first to the second excited state. Express the wavelength of the second photon in terms of \(\lambda_o\).
- Solution
-
The energy of the absorbed photon has to equal the energy of the transition. When the electron transitioned from the n=1 to the n=2 level the energy of the photon was:
\[E_{\text{photon}}=\dfrac{hc}{\lambda_o}=E_2-E_1=\dfrac{h^2}{8mL^2}(2^2-1^2)=3\dfrac{h^2}{8mL^2}\nonumber\]
For the second transition, from n=2 to n=3, similarly the energy of the photon is given by:
\[E_{\text{photon}}=\dfrac{hc}{\lambda_1}=E_3-E_2=\dfrac{h^2}{8mL^2}(3^2-2^2)=5\dfrac{h^2}{8mL^2}\nonumber\]
where we have defined \(\lambda_1\) as the wavelength of the photon absorbed in the second transition. Taking the ratio of the two equations above we get:
\[\dfrac{\lambda_1}{\lambda_o}=\dfrac{3}{5}\Rightarrow \lambda_1=\dfrac{3}{5}\lambda_o\nonumber\]
It makes sense that the second wavelength is shorter than the first. The energy levels are getting further apart, thus, higher energy photons with shorter wavelengths are required to make transitions between increasing neighboring energy levels.