5.15: Changing the Distance Between the Plates of a Capacitor

If you gradually increase the distance between the plates of a capacitor (although always keeping it sufficiently small so that the field is uniform) does the intensity of the field change or does it stay the same? If the former, does it increase or decrease?

The answers to these questions depends

1. on whether, by the field, you are referring to the $E$-field or the $D$-field;
2. on whether the plates are isolated or if they are connected to the poles of a battery.

We shall start by supposing that the plates are isolated.

In this case the charge on the plates is constant, and so is the charge density. Gauss’s law requires that $D = \sigma$, so that $D$remains constant. And, since the permittivity hasn’t changed, $E$ also remains constant.

The potential difference across the plates is $Ed$, so, as you increase the plate separation, so the potential difference across the plates in increased. The capacitance decreases from $\epsilon$A/d₁ to $\epsilon A/d_2$ and the energy stored in the capacitor increases from $\frac{Ad_1\sigma^2}{2\epsilon}\text{ to }\frac{Ad_2\sigma^2}{2\epsilon}$. This energy derives from the work done in separating the plates.

Now let’s suppose that the plates are connected to a battery of EMF $V$, with air or a vacuum between the plates. At first, the separation is $d_1$. The magnitudes of $E$ and $D$are, respectively, $V/d_1$ and $\epsilon_0 V/d_1$. When we have increased the separation to $d_2$, the potential difference across the plates has not changed; it is still the EMF $V$ of the battery. The electric field, however, is now only $E = V/d_2$ and $D = \epsilon_0 V/d_2$. But Gauss’s law still dictates that $D = \sigma$, and therefore the charge density, and the total charge on the plates, is less than it was before. It has gone into the battery. In other words, in doing work by separating the plates we have recharged the battery. The energy stored in the capacitor was originally $\frac{\epsilon_0AV^2}{2d_1}$; it is now only $\frac{\epsilon_0AV^2}{2d_2}$. Thus the energy held in the capacitor has been reduced by $\frac{1}{2}\epsilon_0AV^2\left (\frac{1}{d_1}-\frac{1}{d_2}\right )$.

The charge originally held by the capacitor was $\frac{\epsilon_0AV}{d_1}$. After the plate separation has been increased to d₂ the charge held is $\frac{\epsilon_0AV}{d_1}$. The difference, $\epsilon_0AV\left (\frac{1}{d_1}-\frac{1}{d_2}\right )$, is the charge that has gone into the battery. The energy, or work, required to force this amount of charge into the battery against its EMF $V$ is $\epsilon_0AV^2\left (\frac{1}{d_1}-\frac{1}{d_2}\right )$. Half of this came from the loss in energy held by the capacitor (see above). The other half presumably came from the mechanical work you did in separating the plates. Let’s see if we can verify this.

When the plate separation is $x$, the force between the plates is $\frac{1}{2}QE$ which is $\frac{1}{2}\frac{\epsilon_0AV}{x}\cdot \frac{V}{x}\text{ or }\frac{\epsilon_0AV^2}{2x^2}$. The work required to increase $x$ from $d_1$ to $d_2$ is $\frac{\epsilon_0AV^2}{2}\int_{d_1}^{d_2}\frac{dx}{x^2}$, which is indeed $\frac{1}{2}\epsilon_0AV^2\left (\frac{1}{d_1}-\frac{1}{d_2}\right )$. Thus this amount of mechanical work, plus an equal amount of energy from the capacitor, has gone into recharging the battery. Expressed otherwise, the work done in separating the plates equals the work required to charge the battery minus the decrease in energy stored by the capacitor.

Perhaps we have invented a battery charger (Figure $V.$19)!

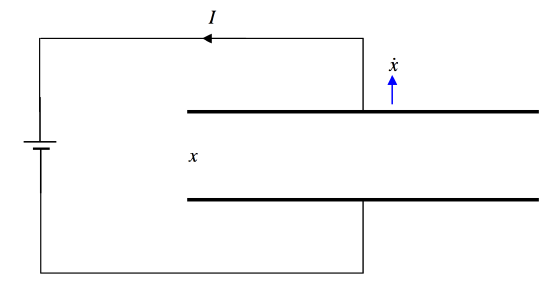
$\text{FIGURE V.19}$

When the plate separation is $x$, the charge stored in the capacitor is $Q=\frac{\epsilon_0AV}{x}$. If $x$ is increased at a rate $\dot x$, $Q$ will increase at a rate $\dot Q=-\frac{\epsilon_0AV\dot x}{x^2}$. That is, the capacitor will discharge (because $\dot Q$ is negative), and a current $I=\frac{\epsilon_0AV\dot x}{x^2}$ will flow counterclockwise in the circuit. (Verify that this expression is dimensionally correct for current.)