2.6: The Light Cone
( \newcommand{\kernel}{\mathrm{null}\,}\)
Given an event P, we can now classify all the causal relationships in which P can participate. In Newtonian physics, these relationships fell into two classes: P could potentially cause any event that lay in its future, and could have been caused by any event in its past. In a Lorentz spacetime, we have a trichotomy rather than a dichotomy. There is a third class of events that are too far away from P in space, and too close in time, to allow any cause and effect relationship, since causality’s maximum velocity is c. Since we’re working in units in which c=1, the boundary of this set is formed by the lines with slope ±1 on a (t,x) plot. This is referred to as the light cone, and in the generalization from 1+1 to 3+1 dimensions, it literally becomes a (four-dimensional) cone. The terminology comes from the fact that light happens to travel at c, the maximum speed of cause and effect. If we make a cut through the cone defined by a surface of constant time in P’s future, the resulting section is a sphere (analogous to the circle formed by cutting a three-dimensional cone), and this sphere is interpreted as the set of events on which P could have had a causal effect by radiating a light pulse outward in all directions.
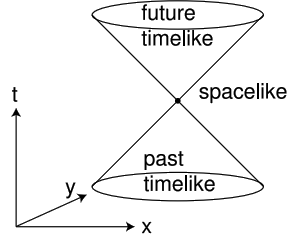
Events lying inside one another’s light cones are said to have a timelike relationship. Events outside each other’s light cones are spacelike in relation to one another, and in the case where they lie on the surfaces of each other’s light cones the term is lightlike.
The light cone plays the same role in the Lorentz geometry that the circle plays in Euclidean geometry. The truth or falsehood of propositions in Euclidean geometry remains the same regardless of how we rotate the figures, and this is expressed by Euclid’s E3 asserting the existence of circles, which remain invariant under rotation. Similarly, Lorentz boosts preserve light cones and truth of propositions in a Lorentz frame.
Exercise 2.6.1
Self-check: Under what circumstances is the time-ordering of events P and Q preserved under a Lorentz boost?
In a uniform Lorentz spacetime, all the light cones line up like soldiers with their axes parallel with one another. When gravity is present, however, this uniformity is disturbed in the vicinity of the masses that constitute the sources. The light cones lying near the sources tip toward the sources. Superimposed on top of this gravitational tipping together, recent observations have demonstrated a systematic tipping-apart effect which becomes significant on cosmological distance scales. The parameter Λ that sets the strength of this effect is known as the cosmological constant. The cosmological constant is not related to the presence of any sources (such as negative masses), and can be interpreted instead as a tendency for space to expand over time on its own initiative. In the present era, the cosmological constant has overpowered the gravitation of the universe’s mass, causing the expansion of the universe to accelerate.
Exercise 2.6.2: Tipping Light Cones
In the bottom panel of Figure 2.3.3, can an observer look at the properties of the spacetime in her immediate vicinity and tell how much her light cones are tipping, and in which direction? Compare with Figure 1.5.9.

Example 14: A Newtonian Black hole
In the case of a black hole, the light cone tips over so far that the entire future timelike region lies within the black hole. If an observer is present at such an event, then that observer’s entire potential future lies within the black hole, not outside it. By expanding on the logical consequences of this statement, we arrive at an example of relativity’s proper interpretation as a theory of causality, not a theory of objects exerting forces on one another as in Newton’s vision of action at a distance, or Lorentz’s original ether-drag interpretation of the factor γ, in which length contraction arose from a physical strain imposed on the atoms composing a physical body.
Imagine a black hole from a Newtonian point of view, as proposed in 1783 by geologist John Michell. Setting the escape velocity equal to the speed of light, we find that this will occur for any gravitating spherical body compact enough to have
Mr>c22G.
A fully relativistic argument, as given in Section 6.2, agrees on
Mr∝c2G
which is fixed by units. The correct unitless factor depends on the definition of r, which is flexible in general relativity.) A flash of light emitted from the surface of such a Newtonian black hole would fall back down like water from a fountain, but it would nevertheless be possible for physical objects to escape, e.g., if they were lifted out in a bucket dangling from a cable. If the cable is to support its own weight, it must have a tensile strength per unit density of at least c22, which is about ten orders of magnitude greater than that of carbon nanotube fibers. (The factor of 12 is not to be taken seriously, since it comes from a nonrelativistic calculation.)
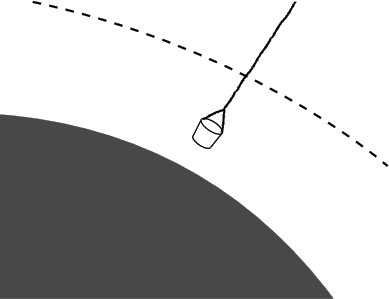
The cause-and-effect interpretation of relativity tells us that this Newtonian picture is incorrect. A physical object that approaches to within a distance r of a concentration of mass M, with Mr sufficiently large, has no causal future lying at larger values of r. The conclusion is that there is a limit on the tensile strength of any substance, imposed purely by general relativity, and we can state this limit without having to know anything about the physical nature of the interatomic forces. A more complete treatment of the tension in the rope is given in example 5. Cf. also problem 4 and section 3.5, as well as some references given in the remark following problem 4.
Velocity Addition
In classical physics, velocities add in relative motion. For example, if a boat moves relative to a river, and the river moves relative to the land, then the boat’s velocity relative to the land is found by vector addition. This linear behavior cannot hold relativistically. For example, if a spaceship is moving at 0.60c relative to the earth, and it launches a probe at 0.60c relative to itself, we can’t have the probe moving at 1.20c relative to the earth, because this would be greater than the maximum speed of cause and effect, c. To see how to add velocities relativistically, we start by rewriting the Lorentz transformation as the matrix
(coshηsinhηsinhηcoshη),
where
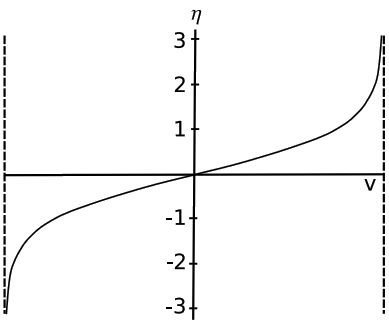
η=tanh−1v
is called the rapidity. We are guaranteed that the matrix can be written in this form, because its area-preserving property says that the determinant equals 1, and cosh2 η −sinh2 η = 1 is an identity of the hyperbolic trig functions. It is now straightforward to verify that multiplication of two matrices of this form gives a third matrix that is also of this form, with
η=η1+η2.
In other words, rapidities add linearly; velocities don’t. In the example of the spaceship and the probe, the rapidities add as
tanh−10.60+tanh−10.60=0.693+0.693=1.386
giving the probe a velocity of tanh 1.386 = 0.88 relative to the earth. Any number of velocities can be added in this way,
η1+η2+…+ηn.
Exercise 2.6.3: Rapidity
Interpret the asymptotes of the graph in Figure 2.3.5.
Example 15: Bell’s spaceship paradox
A difficult philosophical question is whether the time dilation and length contractions predicted by relativity are “real.” This depends, of course, on what one means by “real.” They are frame-dependent, i.e., observers in different frames of reference disagree about them. But this doesn’t tell us much about their reality, since velocities are frame-dependent in Newtonian mechanics, but nobody worries about whether velocities are real. John Bell (1928-1990) proposed the following thought experiment to physicists in the CERN cafeteria, and found that nearly all of them got it wrong. He took this as evidence that their intuitions had been misguided by the standard way of approaching this question of the reality of Lorentz contractions.
Let spaceships A and B accelerate as shown in Figure 2.3.6 along a straight line. Observer C does not accelerate. The accelerations, as judged by C, are constant, and equal for the two ships. Each ship is equipped with a yard-arm, and a thread is tied between the two arms. Does the thread break, due to Lorentz contraction? (We assume that the acceleration is gentle enough that the thread does not break simply because of its own inertia.)
The popular answer in the CERN cafeteria was that the thread would not break, the reasoning being that Lorentz contraction is a frame-dependent effect, and no such contraction would be observed in A and B’s frame. The ships maintain a constant distance from one another, so C merely disagrees with A and B about the length of the thread, as well as other lengths like the lengths of the spaceships.
The error in this reasoning is that the accelerations of A and B were specified to be equal and constant in C’s frame, not in A and B’s. Bell’s interpretation is that the frame-dependence is a distraction, that Lorentz contraction is in some sense a real effect, and that it is therefore immediately clear that the thread must break, without even having to bother going into any other frame. To convince his peers in the cafeteria, however, Bell presumably needed to satisfy them as to the specific errors in their reasoning, and this requires that we consider the frame-dependence explicitly.
We can first see that it is impossible, in general, for different observers to agree about what is meant by constant acceleration. Suppose that A and B agree with C about the constancy of their acceleration. Then A and B experience a voyage in which the rapidities of the stars around them (and of observer C) increase linearly with time. As the rapidity approaches infinity, both C and the stars approach the speed of light. But since A and C agree on the magnitude of their velocity relative to one another, this means that A’s velocity as measured by C must approach c, and this contradicts the premise that C observes constant acceleration for both ships. Therefore A and B do not consider their own accelerations to be constant.
A and B do not agree with C about simultaneity, and since they also do not agree that their accelerations are constant, they do not consider their own accelerations to be equal at a given moment of time. Therefore the string changes its length, and this is consistent with Bell’s original, simple answer, which did not require comparing different frames of reference. To establish that the string comes under tension, rather than going slack, we can apply the equivalence principle. By the equivalence principle, any experiments done by A and B give the same results as if they were immersed in a gravitational field. The leading ship B sees A as experiencing a gravitational time dilation. According to B, the slowpoke A isn’t accelerating as rapidly as it should, causing the string to break.
These ideas are closely related to the fact that general relativity does not admit any spacetime that can be interpreted as a uniform gravitational field (see problem 7).
Logic
The trichotomous classification of causal relationships has interesting logical implications. In classical Aristotelian logic, every proposition is either true or false, but not both, and given propositions p and q, we can form propositions such as p ∧ q (both p and q) or p ∨ q (either p or q). Propositions about physical phenomena can only be verified by observation. Let p be the statement that a certain observation carried out at event P gives a certain result, and similarly for q at Q. If PQ is spacelike, then the truth or falsehood of p ∧ q cannot be checked by physically traveling to P and Q, because no observer would be able to attend both events. The truth-value of p ∧ q is unknown to any observer in the universe until a certain time, at which the relevant information has been able to propagate back and forth. What if P and Q lie inside two different black holes? Then the truth-value of p ∧ q can never be determined by any observer. Another example is the case in which P and Q are separated by such a great distance that, due to the accelerating expansion of the universe, their future light cones do not overlap.
We conclude that Aristotelian logic cannot be appropriately applied to relativistic observation in this way. Some workers attempting to construct a quantum-mechanical theory of gravity have suggested an even more radically observer-dependent logic, in which different observers may contradict one another on the truth-value of a single proposition p1, unless they agree in advance on the list p2, p3, . . . of all the other propositions that they intend to test as well. We’ll return to these questions later.


