11.E: Particle Physics and Cosmology (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
11.1 Introduction to Particle Physics
1. What are the four fundamental forces? Briefly describe them.
2. Distinguish fermions and bosons using the concepts of indistiguishability and exchange symmetry.
3. List the quark and lepton families
4. Distinguish between elementary particles and antiparticles. Describe their interactions.
11.2 Particle Conservation Laws
5. What are six particle conservation laws? Briefly describe them.
6. In general, how do we determine if a particle reaction or decay occurs?
7. Why might the detection of particle interaction that violates an established particle conservation law be considered a good thing for a scientist?
11.3 Quarks
8. What are the six known quarks? Summarize their properties.
9. What is the general quark composition of a baryon? Of a meson?
10. What evidence exists for the existence of quarks?
11. Why do baryons with the same quark composition sometimes differ in their rest mass energies?
11.4 Particle Accelerators and Detectors
12. Briefly compare the Van de Graaff accelerator, linear accelerator, cyclotron, and synchrotron accelerator.
13. Describe the basic components and function of a typical colliding beam machine.
14. What are the subdetectors of the Compact Muon Solenoid experiment? Briefly describe them.
15. What is the advantage of a colliding-beam accelerator over one that fires particles into a fixed target?
16. An electron appears in the muon detectors of the CMS. How is this possible?
11.5 The Standard Model
17. What is the Standard Model? Express your answer in terms of the four fundamental forces and exchange particles.
18. Draw a Feynman diagram to represents annihilation of an electron and positron into a photon.
19. What is the motivation behind grand unification theories?
20. If a theory is developed that unifies all four forces, will it still be correct to say that the orbit of the Moon is determined by the gravitational force? Explain why.
21. If the Higgs boson is discovered and found to have mass, will it be considered the ultimate carrier of the weak force? Explain your response.
22. One of the common decay modes of the Λ0 is Λ0→π−+p. Even though only hadrons are involved in this decay, it occurs through the weak nuclear force. How do we know that this decay does not occur through the strong nuclear force?
11.6 The Big Bang
23. What is meant by cosmological expansion? Express your answer in terms of a Hubble graph and the red shift of distant starlight.
24. Describe the balloon analogy for cosmological expansion. Explain why it only appears that we are at the center of expansion of the universe.
25. Distances to local galaxies are determined by measuring the brightness of stars, called Cepheid variables, that can be observed individually and that have absolute brightnesses at a standard distance that are well known. Explain how the measured brightness would vary with distance, as compared with the absolute brightness.
11.7 Evolution of the Early Universe
26. What is meant by a “cosmological model of the early universe?” Briefly describe this model in terms of the four fundamental forces.
27. Describe two pieces of evidence that support the Big Bang model.
28. In what sense are we, as Newton once said, “a boy playing on the sea-shore”? Express your answer in terms of the concepts of dark matter and dark energy.
29. If some unknown cause of redshift—such as light becoming “tired” from traveling long distances through empty space—is discovered, what effect would that have on cosmology?
30. In the past, many scientists believed the universe to be infinite. However, if the universe is infinite, then any line of sight should eventually fall on a star’s surface and the night sky should be very bright. How is this paradox resolved in modern cosmology?
Problems
11.1 Introduction to Particle Physics
31. How much energy is released when an electron and a positron at rest annihilate each other? (For particle masses, see Table 11.1.)
32. If 1.0×1030MeV of energy is released in the annihilation of a sphere of matter and antimatter, and the spheres are equal mass, what are the masses of the spheres?
33. When both an electron and a positron are at rest, they can annihilate each other according to the reaction e−+e+→γ+γ. In this case, what are the energy, momentum, and frequency of each photon?
34. What is the total kinetic energy carried away by the particles of the following decays?
(a) π0→γ+γ
(b) K0→π++π−
(c) ∑+→n+π+
(d) ∑0→Λ0+γ.
11.2 Particle Conservation Laws
35. Which of the following decays cannot occur because the law of conservation of lepton number is violated?
(a) n→p+e−
(b) μ+→e++¯νe
(c) π+→e++νe+¯νμ
(d) p→n+e++νe
(e) π−→e−+¯νe
(f) μ−→e−+¯νe+νμ
(g) Λ0→π−+p
(h) K+→μ++νμ
36. Which of the following reactions cannot because the law of conservation of strangeness is violated?
(a) p+n→p+p+π−
(b) p+n→p+p+K−
(c) K−+p→K−+∑+
(d) π−+p→K++∑−
(e) K−+p→Ξ0+K++π−
(f) K−+p→Ξ0+π−+π−
(g) π++p→∑++K+
(h) π−+n→K−+Λ0
37. Identify one possible decay for each of the following antiparticles:
(a) ˉn,
(b) ˉΛ0,
(c) Ω+,
(d) K−, and
(e) ¯∑.
38. Each of the following strong nuclear reactions is forbidden. Identify a conservation law that is violated for each one.
(a) p+ˉp→p+n+ˉp
(b) p+n→p+ˉp+n+π+
(c) π−+p→∑++K−
(d) K−+p→Λ0+n
11.3 Quarks
39. Based on quark composition of a proton, show that its charge is +1.
40. Based on the quark composition of a neutron, show that is charge is 0.
41. Argue that the quark composition given in Table 11.5 for the positive kaon is consistent with the known charge, spin, and strangeness of this baryon.
42. Mesons are formed from the following combinations of quarks (subscripts indicate color and (AR=antired):(dR,¯dAR),(sG,¯uAG), and (sR,¯sAR).
(a) Determine the charge and strangeness of each combination.
(b) Identify one or more mesons formed by each quark-antiquark combination.
43. Why can’t either set of quarks shown below form a hadron?
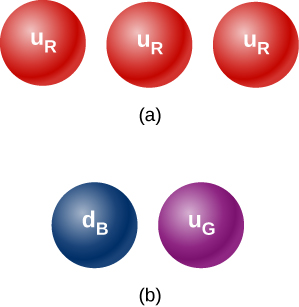
44. Experimental results indicate an isolate particle with charge +2/3—an isolated quark. What quark could this be? Why would this discovery be important?
45. Express the β decays n→p+e−+ˉν and p→n+e++ν in terms of β decays of quarks. Check to see that the conservation laws for charge, lepton number, and baryon number are satisfied by the quark β decays.
11.4 Particle Accelerators and Detectors
46. A charged particle in a 2.0-T magnetic field is bent in a circle of radius 75 cm. What is the momentum of the particle?
47. A proton track passes through a magnetic field with radius of 50 cm. The magnetic field strength is 1.5 T. What is the total energy of the proton?
48. Derive the equation p=0.3Br using the concepts of centripetal acceleration (Motion in Two and Three Dimensions) and relativistic momentum (Relativity)
49. Assume that beam energy of an electron-positron collider is approximately 4.73 GeV. What is the total mass (W) of a particle produced in the annihilation of an electron and positron in this collider? What meson might be produced?
50. At full energy, protons in the 2.00-km-diameter Fermilab synchrotron travel at nearly the speed of light, since their energy is about 1000 times their rest mass energy.
(a) How long does it take for a proton to complete one trip around?
(b) How many times per second will it pass through the target area?
51. Suppose a W− created in a particle detector lives for 5.00×10−25s. What distance does it move in this time if it is traveling at 0.900c? (Note that the time is longer than the given W− lifetime, which can be due to the statistical nature of decay or time dilation.)
52. What length track does a π+ traveling at 0.100c leave in a bubble chamber if it is created there and lives for 2.60×10−8s? (Those moving faster or living longer may escape the detector before decaying.)
53. The 3.20-km-long SLAC produces a beam of 50.0-GeV electrons. If there are 15,000 accelerating tubes, what average voltage must be across the gaps between them to achieve this energy?
11.5 The Standard Model
54. Using the Heisenberg uncertainly principle, determine the range of the weak force if this force is produced by the exchange of a Z boson.
55. Use the Heisenberg uncertainly principle to estimate the range of a weak nuclear decay involving a graviton.
56. (a) The following decay is mediated by the electroweak force: p→n+e++νe. Draw the Feynman diagram for the decay.
(b) The following scattering is mediated by the electroweak force: νe+e−→νe+e−. Draw the Feynman diagram for the scattering.
57. Assuming conservation of momentum, what is the energy of each γ ray produced in the decay of a neutral pion at rest, in the reaction π0→γ+γ?
58. What is the wavelength of a 50-GeV electron, which is produced at SLAC? This provides an idea of the limit to the detail it can probe.
59. The primary decay mode for the negative pion is π−→μ−+¯νμ.
(a) What is the energy release in MeV in this decay?
(b) Using conservation of momentum, how much energy does each of the decay products receive, given the π− is at rest when it decays? You may assume the muon antineutrino is massless and has momentum p=E/c, just like a photon.
60. Suppose you are designing a proton decay experiment and you can detect 50 percent of the proton decays in a tank of water.
(a) How many kilograms of water would you need to see one decay per month, assuming a lifetime of 1031y?
(b) How many cubic meters of water is this?
(c) If the actual lifetime is 1033y, how long would you have to wait on an average to see a single proton decay?
11.6 The Big Bang
61. If the speed of a distant galaxy is 0.99c, what is the distance of the galaxy from an Earth-bound observer?
62. The distance of a galaxy from our solar system is 10 Mpc.
(a) What is the recessional velocity of the galaxy?
(b) By what fraction is the starlight from this galaxy redshifted (that is, what is its z value)?
63. If a galaxy is 153 Mpc away from us, how fast do we expect it to be moving and in what direction?
64. On average, how far away are galaxies that are moving away from us at 2.0% of the speed of light?
65. Our solar system orbits the center of the Milky Way Galaxy. Assuming a circular orbit 30,000 ly in radius and an orbital speed of 250 km/s, how many years does it take for one revolution? Note that this is approximate, assuming constant speed and circular orbit, but it is representative of the time for our system and local stars to make one revolution around the galaxy.
66. (a) What is the approximate velocity relative to us of a galaxy near the edge of the known universe, some 10 Gly away?
(b) What fraction of the speed of light is this? Note that we have observed galaxies moving away from us at greater than 0.9c.
67. (a) Calculate the approximate age of the universe from the average value of the Hubble constant, H0=20km/s⋅Mly. To do this, calculate the time it would take to travel 0.307 Mpc at a constant expansion rate of 20 km/s.
(b) If somehow acceleration occurs, would the actual age of the universe be greater or less than that found here? Explain.
68. The Andromeda Galaxy is the closest large galaxy and is visible to the naked eye. Estimate its brightness relative to the Sun, assuming it has luminosity 1012 times that of the Sun and lies 0.613 Mpc away.
69. Show that the velocity of a star orbiting its galaxy in a circular orbit is inversely proportional to the square root of its orbital radius, assuming the mass of the stars inside its orbit acts like a single mass at the center of the galaxy. You may use an equation from a previous chapter to support your conclusion, but you must justify its use and define all terms used.
Additional Problems
70. Experimental results suggest that a muon decays to an electron and photon. How is this possible?
71. Each of the following reactions is missing a single particle. Identify the missing particle for each reaction.
(a) p+ˉp→n+?
(b) p+p→p+Λ0+?
(c) π−+p→∑−+?
(d) K−+n→Λ0+?
(e) τ+→e++νe+?
(f) ¯νe+p→n+?
72. Because of energy loss due to synchrotron radiation in the LHC at CERN, only 5.00 MeV is added to the energy of each proton during each revolution around the main ring. How many revolutions are needed to produce 7.00-TeV (7000 GeV) protons, if they are injected with an initial energy of 8.00 GeV?
73. A proton and an antiproton collide head-on, with each having a kinetic energy of 7.00 TeV (such as in the LHC at CERN). How much collision energy is available, taking into account the annihilation of the two masses? (Note that this is not significantly greater than the extremely relativistic kinetic energy.)
74. When an electron and positron collide at the SLAC facility, they each have 50.0-GeV kinetic energies. What is the total collision energy available, taking into account the annihilation energy? Note that the annihilation energy is insignificant, because the electrons are highly relativistic.
75. The core of a star collapses during a supernova, forming a neutron star. Angular momentum of the core is conserved, so the neutron star spins rapidly. If the initial core radius is 5.0×105km and it collapses to 10.0 km, find the neutron star’s angular velocity in revolutions per second, given the core’s angular velocity was originally 1 revolution per 30.0 days.
76. Using the solution from the previous problem, find the increase in rotational kinetic energy, given the core’s mass is 1.3 times that of our Sun. Where does this increase in kinetic energy come from?
77. (a) What Hubble constant corresponds to an approximate age of the universe of 1010 y? To get an approximate value, assume the expansion rate is constant and calculate the speed at which two galaxies must move apart to be separated by 1 Mly (present average galactic separation) in a time of 1010y.
(b) Similarly, what Hubble constant corresponds to a universe approximately 2×1010 years old?
Challenge Problems
78. Electrons and positrons are collided in a circular accelerator. Derive the expression for the center-of-mass energy of the particle.
79. The intensity of cosmic ray radiation decreases rapidly with increasing energy, but there are occasionally extremely energetic cosmic rays that create a shower of radiation from all the particles they create by striking a nucleus in the atmosphere. Suppose a cosmic ray particle having an energy of 1010GeV converts its energy into particles with masses averaging 200MeV/c2.
(a) How many particles are created?
(b) If the particles rain down on a 1.00−km2 area, how many particles are there per square meter?
80. (a) Calculate the relativistic quantity γ=11√1−v2/c2 for 1.00-TeV protons produced at Fermilab.
(b) If such a proton created a π+ having the same speed, how long would its life be in the laboratory?
(c) How far could it travel in this time?
81. Plans for an accelerator that produces a secondary beam of K mesons to scatter from nuclei, for the purpose of studying the strong force, call for them to have a kinetic energy of 500 MeV.
(a) What would the relativistic quantity γ=1√1−v2/c2 be for these particles?
(b) How long would their average lifetime be in the laboratory?
(c) How far could they travel in this time?
82. In supernovae, neutrinos are produced in huge amounts. They were detected from the 1987A supernova in the Magellanic Cloud, which is about 120,000 light-years away from Earth (relatively close to our Milky Way Galaxy). If neutrinos have a mass, they cannot travel at the speed of light, but if their mass is small, their velocity would be almost that of light.
(a) Suppose a neutrino with a 7−eV/c2 mass has a kinetic energy of 700 keV. Find the relativistic quantity γ=1√1−v2/c2 for it.
(b) If the neutrino leaves the 1987A supernova at the same time as a photon and both travel to Earth, how much sooner does the photon arrive? This is not a large time difference, given that it is impossible to know which neutrino left with which photon and the poor efficiency of the neutrino detectors. Thus, the fact that neutrinos were observed within hours of the brightening of the supernova only places an upper limit on the neutrino’s mass. (Hint: You may need to use a series expansion to find v for the neutrino, since its γ is so large.)
83. Assuming a circular orbit for the Sun about the center of the Milky Way Galaxy, calculate its orbital speed using the following information: The mass of the galaxy is equivalent to a single mass 1.5×1011 times that of the Sun (or 3×1041kg), located 30,000 ly away.
84. (a) What is the approximate force of gravity on a 70-kg person due to the Andromeda Galaxy, assuming its total mass is 1013 that of our Sun and acts like a single mass 0.613 Mpc away?
(b) What is the ratio of this force to the person’s weight? Note that Andromeda is the closest large galaxy.
85. (a) A particle and its antiparticle are at rest relative to an observer and annihilate (completely destroying both masses), creating two γ rays of equal energy. What is the characteristic γ-ray energy you would look for if searching for evidence of proton-antiproton annihilation? (The fact that such radiation is rarely observed is evidence that there is very little antimatter in the universe.)
(b) How does this compare with the 0.511-MeV energy associated with electron-positron annihilation?
86. The peak intensity of the CMBR occurs at a wavelength of 1.1 mm.
(a) What is the energy in eV of a 1.1-mm photon?
(b) There are approximately 109 photons for each massive particle in deep space. Calculate the energy of 109 such photons.
(c) If the average massive particle in space has a mass half that of a proton, what energy would be created by converting its mass to energy?
(d) Does this imply that space is “matter dominated”? Explain briefly.
87. (a) Use the Heisenberg uncertainty principle to calculate the uncertainty in energy for a corresponding time interval of 10−43s.
(b) Compare this energy with the 1019GeV unification-of-forces energy and discuss why they are similar.


