14.E: Thermal Physics (Exercises)
- Last updated
- Save as PDF
- Page ID
- 103216
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
9.1: Temperature
1. What does it mean to say that two systems are in thermal equilibrium?
2. Give an example of a physical property that varies with temperature and describe how it is used to measure temperature.
3. When a cold alcohol thermometer is placed in a hot liquid, the column of alcohol goes down slightly before going up. Explain why.
4. If you add boiling water to a cup at room temperature, what would you expect the final equilibrium temperature of the unit to be? You will need to include the surroundings as part of the system. Consider the zeroth law of thermodynamics.
9.2: The Ideal Gas Law
5. Under what circumstances would you expect a gas to behave significantly differently than predicted by the ideal gas law?
6. A constant-volume gas thermometer contains a fixed amount of gas. What property of the gas is measured to indicate its temperature?
9.3: Heat
7. How is heat transfer related to temperature?
8. Describe a situation in which heat transfer occurs. What are the resulting forms of energy?
9. When heat transfers into a system, is the energy stored as heat? Explain briefly.
9.4: Heat Transfer Methods
10. What are the main methods of heat transfer from the hot core of Earth to its surface? From Earth’s surface to outer space?
11. When our bodies get too warm, they respond by sweating and increasing blood circulation to the surface to transfer thermal energy away from the core. What effect will this have on a person in a 40.0ºC hot tub?
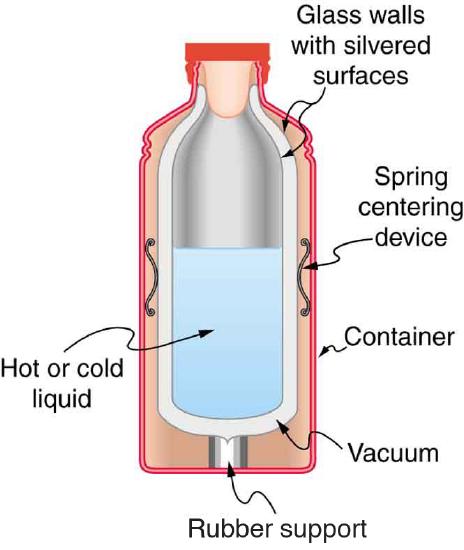
12. Figure \(\PageIndex{1}\) shows a cut-away drawing of a thermos bottle (also known as a Dewar flask), which is a device designed specifically to slow down all forms of heat transfer. Explain the functions of the various parts, such as the vacuum, the silvering of the walls, the thin-walled long glass neck, the rubber support, the air layer, and the stopper.
9.5: Temperature Change and Heat Capacity
13. What three factors affect the heat transfer that is necessary to change an object’s temperature?
14. The brakes in a car increase in temperature by \(\Delta T\) when bringing the car to rest from a speed \(v\). How much greater would \(\Delta T\) be if the car initially had twice the speed? You may assume the car to stop sufficiently fast so that no heat transfers out of the brakes.
9.6: Phase Change and Latent Heat
15. Heat transfer can cause temperature and phase changes. What else can cause these changes?
16. How does the latent heat of fusion of water help slow the decrease of air temperatures, perhaps preventing temperatures from falling significantly below \(0^{\circ} \mathrm{C}\), in the vicinity of large bodies of water?
17. What is the temperature of ice right after it is formed by freezing water?
18. If you place \(0^{\circ} \mathrm{C}\) ice into \(0^{\circ} \mathrm{C}\) water in an insulated container, what will happen? Will some ice melt, will more water freeze, or will neither take place?
19. What effect does condensation on a glass of ice water have on the rate at which the ice melts? Will the condensation speed up the melting process or slow it down?
20. In very humid climates where there are numerous bodies of water, such as in Florida, it is unusual for temperatures to rise above about 35ºC(95ºF). In deserts, however, temperatures can rise far above this. Explain how the evaporation of water helps limit high temperatures in humid climates.
21. In winters, it is often warmer in San Francisco than in nearby Sacramento, 150 km inland. In summers, it is nearly always hotter in Sacramento. Explain how the bodies of water surrounding San Francisco moderate its extreme temperatures.
22. Putting a lid on a boiling pot greatly reduces the heat transfer necessary to keep it boiling. Explain why.
23. Freeze-dried foods have been dehydrated in a vacuum. During the process, the food freezes and must be heated to facilitate dehydration. Explain both how the vacuum speeds up dehydration and why the food freezes as a result.
24. When still air cools by radiating at night, it is unusual for temperatures to fall below the dew point. Explain why.
25. In a physics classroom demonstration, an instructor inflates a balloon by mouth and then cools it in liquid nitrogen. When cold, the shrunken balloon has a small amount of light blue liquid in it, as well as some snow-like crystals. As it warms up, the liquid boils, and part of the crystals sublimate, with some crystals lingering for awhile and then producing a liquid. Identify the blue liquid and the two solids in the cold balloon. Justify your identifications using data from Table 9.6.1.
9.7: The First Law of Thermodynamics
26. Describe the photo of the tea kettle at the beginning of this section in terms of heat transfer, work done, and internal energy. How is heat being transferred? What is the work done and what is doing it? How does the kettle maintain its internal energy?
27. The first law of thermodynamics and the conservation of energy are clearly related. How do they differ in the types of energy considered?
28. Heat transfer \(Q\) and work done \(W\) are always energy in transit, whereas internal energy \(U\) is energy stored in a system. Give an example of each type of energy, and state specifically how it is either in transit or resides in a system.
29. How do heat transfer and internal energy differ? In particular, which can be stored as such in a system and which cannot?
30. If you run down some stairs and stop, what happens to your kinetic energy and your initial gravitational potential energy?
31. Give an explanation of how food energy (calories) can be viewed as molecular potential energy (consistent with the atomic and molecular definition of internal energy).
32. Identify the type of energy transferred to your body in each of the following as either internal energy, heat transfer, or doing work:
(a) basking in sunlight;
(b) eating food;
(c) riding an elevator to a higher floor.
9.8: The First Law of Thermodynamics and Heat Engine Processes
33. A great deal of effort, time, and money has been spent in the quest for the so-called perpetual-motion machine, which is defined as a hypothetical machine that operates or produces useful work indefinitely and/or a hypothetical machine that produces more work or energy than it consumes. Explain, in terms of heat engines and the first law of thermodynamics, why or why not such a machine is likely to be constructed.
34. One method of converting heat transfer into doing work is for heat transfer into a gas to take place, which expands, doing work on a piston, as shown in the figure below.
(a) Is the heat transfer converted directly to work in an isobaric process, or does it go through another form first? Explain your answer.
(b) What about in an isothermal process?
(c) What about in an adiabatic process (where heat transfer occurred prior to the adiabatic process)?
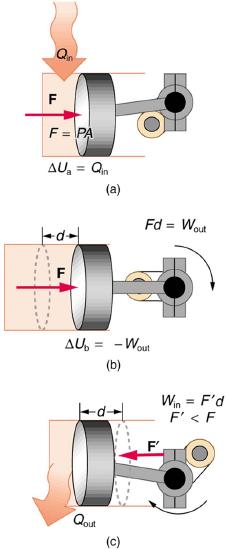
Figure \(\PageIndex{2}\)
35. Would the previous question make any sense for an isochoric process? Explain your answer.
36. We ordinarily say that \(\Delta U=0\) for an isothermal process. Does this assume no phase change takes place? Explain your answer.
37. The temperature of a rapidly expanding gas decreases. Explain why in terms of the first law of thermodynamics. (Hint: Consider whether the gas does work and whether heat transfer occurs rapidly into the gas through conduction.)
38. A real process may be nearly adiabatic if it occurs over a very short time. How does the short time span help the process to be adiabatic?
39. It is unlikely that a process can be isothermal unless it is a very slow process. Explain why. Is the same true for isobaric and isochoric processes? Explain your answer.
9.9: Introduction to the Second Law of Thermodynamics- Heat Engines and Their Efficiency
40. Imagine you are driving a car up Pike’s Peak in Colorado. To raise a car weighing 1000 kilograms a distance of 100 meters would require about a million joules. You could raise a car 12.5 kilometers with the energy in a gallon of gas. Driving up Pike's Peak (a mere 3000-meter climb) should consume a little less than a quart of gas. But other considerations have to be taken into account. Explain, in terms of efficiency, what factors may keep you from realizing your ideal energy use on this trip.
41. Is a temperature difference necessary to operate a heat engine? State why or why not.
42. Definitions of efficiency vary depending on how energy is being converted. Compare the definitions of efficiency for the human body and heat engines. How does the definition of efficiency in each relate to the type of energy being converted into doing work?
43. Why—other than the fact that the second law of thermodynamics says reversible engines are the most efficient—should heat engines employing reversible processes be more efficient than those employing irreversible processes? Consider that dissipative mechanisms are one cause of irreversibility.
9.10: Carnot’s Perfect Heat Engine- The Second Law of Thermodynamics Restated
44. Think about the drinking bird at the beginning of this section (Figure 9.10.1). Although the bird enjoys the theoretical maximum efficiency possible, if left to its own devices over time, the bird will cease “drinking.” What are some of the dissipative processes that might cause the bird’s motion to cease?
45. Can improved engineering and materials be employed in heat engines to reduce heat transfer into the environment? Can they eliminate heat transfer into the environment entirely?
46. Does the second law of thermodynamics alter the conservation of energy principle?
9.11: Applications of Thermodynamics- Heat Pumps and Refrigerators
47. Explain why heat pumps do not work as well in very cold climates as they do in milder ones. Is the same true of refrigerators?
48. In some Northern European nations, homes are being built without heating systems of any type. They are very well insulated and are kept warm by the body heat of the residents. However, when the residents are not at home, it is still warm in these houses. What is a possible explanation?
49. Why do refrigerators, air conditioners, and heat pumps operate most cost-effectively for cycles with a small difference between \(T_{\mathrm{h}}\) and \(T_{\mathrm{c}}\)? (Note that the temperatures of the cycle employed are crucial to its \(C O P\).)
50. Grocery store managers contend that there is less total energy consumption in the summer if the store is kept at a low temperature. Make arguments to support or refute this claim, taking into account that there are numerous refrigerators and freezers in the store.
51. Can you cool a kitchen by leaving the refrigerator door open?
9.12: Entropy and the Second Law of Thermodynamics- Disorder and the Unavailability of Energy
52. Does a gas become more orderly when it liquefies? Does its entropy change? If so, does the entropy increase or decrease? Explain your answer.
53. Explain how water’s entropy can decrease when it freezes without violating the second law of thermodynamics. Specifically, explain what happens to the entropy of its surroundings.
54. Is a uniform-temperature gas more or less orderly than one with several different temperatures? Which is more structured? In which can heat transfer result in work done without heat transfer from another system?
55. Give an example of a spontaneous process in which a system becomes less ordered and energy becomes less available to do work. What happens to the system’s entropy in this process?
56. What is the change in entropy in an adiabatic process? Does this imply that adiabatic processes are reversible? Can a process be precisely adiabatic for a macroscopic system?
57. Does the entropy of a star increase or decrease as it radiates? Does the entropy of the space into which it radiates (which has a temperature of about 3 K) increase or decrease? What does this do to the entropy of the universe?
58. Explain why a building made of bricks has smaller entropy than the same bricks in a disorganized pile. Do this by considering the number of ways that each could be formed (the number of microstates in each macrostate).
9.13: Statistical Interpretation of Entropy and the Second Law of Thermodynamics- The Underlying Explanation
59. Explain why a building made of bricks has smaller entropy than the same bricks in a disorganized pile. Do this by considering the number of ways that each could be formed (the number of microstates in each macrostate).
Problems & Exercises
9.1: Temperature
1. What is the Fahrenheit temperature of a person with a 39.0ºC fever?
Answer
102ºF
2. Frost damage to most plants occurs at temperatures of 28.0ºF or lower. What is this temperature on the Kelvin scale?
3. To conserve energy, room temperatures are kept at 68.0ºF in the winter and 78.0ºF in the summer. What are these temperatures on the Celsius scale?
Answer
20.0ºC and 25.6ºC
4. A tungsten light bulb filament may operate at 2900 K. What is its Fahrenheit temperature? What is this on the Celsius scale?
5. The surface temperature of the Sun is about 5750 K. What is this temperature on the Fahrenheit scale?
Answer
9890ºF
6. One of the hottest temperatures ever recorded on the surface of Earth was 134ºF in Death Valley, CA. What is this temperature in Celsius degrees? What is this temperature in Kelvin?
7. (a) Suppose a cold front blows into your locale and drops the temperature by 40.0 Fahrenheit degrees. How many degrees Celsius does the temperature decrease when there is a 40.0ºF decrease in temperature?
(b) Show that any change in temperature in Fahrenheit degrees is nine-fifths the change in Celsius degrees.
Answer
(a) 22.2ºC
(b) \(\begin{aligned}
\Delta T\left({ }^{\circ} \mathrm{F}\right) &=T_{2}\left({ }^{\circ} \mathrm{F}\right)-T_{1}\left({ }^{\circ} \mathrm{F}\right) \\
&=\frac{9}{5} T_{2}\left({ }^{\circ} \mathrm{C}\right)+32.0^{\circ}-\left(\frac{9}{5} T_{1}\left({ }^{\circ} \mathrm{C}\right)+32.0^{\circ}\right) \\
&=\frac{9}{5}\left(T_{2}\left({ }^{\circ} \mathrm{C}\right)-T_{1}\left({ }^{\circ} \mathrm{C}\right)\right)=\frac{9}{5} \Delta T\left({ }^{\circ} \mathrm{C}\right)
\end{aligned}\)
8. (a) At what temperature do the Fahrenheit and Celsius scales have the same numerical value?
(b) At what temperature do the Fahrenheit and Kelvin scales have the same numerical value?
9.2: The Ideal Gas Law
9. The gauge pressure in your car tires is \(2.50 \times 10^{5} \mathrm{~N} / \mathrm{m}^{2}\) at a temperature of 35.0ºC when you drive it onto a ferry boat to Alaska. What is their gauge pressure later, when their temperature has dropped to –40.0ºC?
Answer
1.62 atm
10. Convert an absolute pressure of \(7.00 \times 10^{5} \mathrm{~N} / \mathrm{m}^{2}\) to gauge pressure in \(\mathrm{lb} / \mathrm{in}^{2}\). (This value was stated to be just less than \(90.0 \ \mathrm{lb} / \mathrm{in}^{2}\) in Example 9.2.1. Is it?)
11. Suppose a gas-filled incandescent light bulb is manufactured so that the gas inside the bulb is at atmospheric pressure when the bulb has a temperature of 20.0ºC.
(a) Find the gauge pressure inside such a bulb when it is hot, assuming its average temperature is 60.0ºC (an approximation) and neglecting any change in volume due to thermal expansion or gas leaks.
(b) The actual final pressure for the light bulb will be less than calculated in part (a) because the glass bulb will expand. What will the actual final pressure be, taking this into account? Is this a negligible difference?
Answer
(a) 0.136 atm
(b) 0.135 atm. The difference between this value and the value from part (a) is negligible.
12. Large helium-filled balloons are used to lift scientific equipment to high altitudes. (a) What is the pressure inside such a balloon if it starts out at sea level with a temperature of 10.0ºC and rises to an altitude where its volume is twenty times the original volume and its temperature is –50.0ºC? (b) What is the gauge pressure? (Assume atmospheric pressure is constant.)
13. In the text, it was shown that \(N / V=2.68 \times 10^{25} \mathrm{~m}^{-3}\) for gas at STP.
(a) Show that this quantity is equivalent to \(N / V=2.68 \times 10^{19} \mathrm{~cm}^{-3}\), as stated.
(b) About how many atoms are there in one \(\mu \mathrm{m}^{3}\) (a cubic micrometer) at STP?
(c) What does your answer to part (b) imply about the separation of atoms and molecules?
14. An airplane passenger has \(100 \mathrm{~cm}^{3}\) of air in his stomach just before the plane takes off from a sea-level airport. What volume will the air have at cruising altitude if cabin pressure drops to \(7.50 \times 10^{4} \mathrm{~N} / \mathrm{m}^{2}\)?
15. An expensive vacuum system can achieve a pressure as low as \(1.00 \times 10^{-7} \mathrm{~N} / \mathrm{m}^{2}\) at 20ºC. How many atoms are there in a cubic centimeter at this pressure and temperature?
16. The number density of gas atoms at a certain location in the space above our planet is about \(1.00 \times 10^{11} \mathrm{~m}^{-3}\), and the pressure is \(2.75 \times 10^{-10} \mathrm{~N} / \mathrm{m}^{2}\) in this space. What is the temperature there?
Answer
−73.9ºC
17. A bicycle tire has a pressure of \(7.00 \times 10^{5} \mathrm{~N} / \mathrm{m}^{2}\) at a temperature of 18.0ºC and contains 2.00 L of gas. What will its pressure be if you let out an amount of air that has a volume of 100 cm3 at atmospheric pressure? Assume tire temperature and volume remain constant.
18. A high-pressure gas cylinder contains 50.0 L of toxic gas at a pressure of \(1.40 \times 10^{7} \mathrm{~N} / \mathrm{m}^{2}\) and a temperature of 25.0ºC. Its valve leaks after the cylinder is dropped. The cylinder is cooled to dry ice temperature (–78.5ºC) to reduce the leak rate and pressure so that it can be safely repaired.
(a) What is the final pressure in the tank, assuming a negligible amount of gas leaks while being cooled and that there is no phase change?
(b) What is the final pressure if one-tenth of the gas escapes?
(c) To what temperature must the tank be cooled to reduce the pressure to 1.00 atm (assuming the gas does not change phase and that there is no leakage during cooling)?
(d) Does cooling the tank appear to be a practical solution?
Answer
(a) 9.14×106 N/m2
(b) 8.23×106 N/m2
(c) 2.16 K
(d) No. The final temperature needed is much too low to be easily achieved for a large object.
19. (a) What is the gauge pressure in a 25.0ºC car tire containing 3.60 mol of gas in a 30.0 L volume?
(b) What will its gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and 25.0ºC? Assume the temperature returns to 25.0ºC and the volume remains constant.
9.10: Carnot’s Perfect Heat Engine- The Second Law of Thermodynamics Restated
20. A certain gasoline engine has an efficiency of 30.0%. What would the hot reservoir temperature be for a Carnot engine having that efficiency, if it operates with a cold reservoir temperature of \(200^{\circ} \mathrm{C}\)?
Solution
403ºC
21. A gas-cooled nuclear reactor operates between hot and cold reservoir temperatures of \(700^{\circ} \mathrm{C}\) and \(27.0^{\circ} \mathrm{C}\).
(a) What is the maximum efficiency of a heat engine operating between these temperatures?
(b) Find the ratio of this efficiency to the Carnot efficiency of a standard nuclear reactor (found in Example 9.10.1).
22. (a) What is the hot reservoir temperature of a Carnot engine that has an efficiency of 42.0% and a cold reservoir temperature of \(27.0^{\circ} \mathrm{C}\)?
(b) What must the hot reservoir temperature be for a real heat engine that achieves 0.700 of the maximum efficiency, but still has an efficiency of 42.0% (and a cold reservoir at \(27.0^{\circ} \mathrm{C}\))?
(c) Does your answer imply practical limits to the efficiency of car gasoline engines?
Solution
(a) 244ºC
(b) 477ºC
(c) Yes, since automobiles engines cannot get too hot without overheating, their efficiency is limited.
23. Steam locomotives have an efficiency of 17.0% and operate with a hot steam temperature of \(425^{\circ} \mathrm{C}\).
(a) What would the cold reservoir temperature be if this were a Carnot engine?
(b) What would the maximum efficiency of this steam engine be if its cold reservoir temperature were \(150^{\circ} \mathrm{C}\)?
24. Practical steam engines utilize \(450^{\circ} \mathrm{C}\) steam, which is later exhausted at \(270^{\circ} \mathrm{C}\).
(a) What is the maximum efficiency that such a heat engine can have?
(b) Since \(270^{\circ} \mathrm{C}\) steam is still quite hot, a second steam engine is sometimes operated using the exhaust of the first. What is the maximum efficiency of the second engine if its exhaust has a temperature of \(150^{\circ} \mathrm{C}\)?
(c) What is the overall efficiency of the two engines? (d) Show that this is the same efficiency as a single Carnot engine operating between \(450^{\circ} \mathrm{C}\) and \(150^{\circ} \mathrm{C}\). Explicitly show how you follow the steps in the Problem-Solving Strategies for Thermodynamics.
Solution
(a) \(E f f_{1}=1-\frac{T_{c, 1}}{T_{\mathrm{h}, 1}}=1-\frac{543 \mathrm{~K}}{723 \mathrm{~K}}=0.249 \text { or } 24.9 \%\)
(b) \(E f f_{2}=1-\frac{423 \mathrm{~K}}{543 \mathrm{~K}}=0.221 \text { or } 22.1 \%\)
(c) \(\begin{align*}
E f f_{1}=1-\frac{T_{\mathrm{c}, \mathrm{l}}}{T_{\mathrm{h}, 1}} \Rightarrow T_{\mathrm{c}, 1}=T_{\mathrm{h}, 1}\left(1,-, e f f_{1}\right) & \text { similarly, } T_{\mathrm{c}, 2}=T_{\mathrm{h}, 2}\left(1-E f f_{2}\right) \\
T_{\mathrm{c}, 2} &=T_{\mathrm{h}, 1}\left(1-E f f_{1}\right)\left(1-E f f_{2}\right) \equiv T_{\mathrm{h}, 1}\left(1-E f f_{\text {overall }}\right)
\end{align*} \)
\(\begin{align*} \text { using } T_{\mathrm{h}, 2}=T_{\mathrm{c}, 1} \text { in above equation gives } \therefore\left(1-E f f_{\text {overall }}\right)=\left(1-E f f_{1}\right)\left(1-E f f_{2}\right) \\[4pt] E f f_{\text {overall }}=1-(1-0.249)(1-0.221)=41.5 \% \end{align*}\)
(d) \(E f f_{\text {overall }}=1-\frac{423 \mathrm{~K}}{723 \mathrm{~K}}=0.415 \text { or } 41.5 \%\)
25. A coal-fired electrical power station has an efficiency of 38%. The temperature of the steam leaving the boiler is \(550^{\circ} \mathrm{C}\). What percentage of the maximum efficiency does this station obtain? (Assume the temperature of the environment is \(20^{\circ} \mathrm{C}\).)
26. Would you be willing to financially back an inventor who is marketing a device that she claims has 25 kJ of heat transfer at 600 K, has heat transfer to the environment at 300 K, and does 12 kJ of work? Explain your answer.
Solution
The heat transfer to the cold reservoir is \(Q_{\mathrm{c}}=Q_{\mathrm{h}}-W=25 \mathrm{~kJ}-12 \mathrm{~kJ}=13 \mathrm{~kJ}\), so the efficiency is \(E f f=1-\frac{Q_{\mathrm{c}}}{Q_{\mathrm{h}}}=1-\frac{13 \mathrm{~kJ}}{25 \mathrm{~kJ}}=0.48\). The Carnot efficiency is \(E f f_{\mathrm{C}}=1-\frac{T_{\mathrm{c}}}{T_{\mathrm{h}}}=1-\frac{300 \mathrm{~K}}{600 \mathrm{~K}}=0.50\). The actual efficiency is 96% of the Carnot efficiency, which is much higher than the best-ever achieved of about 70%, so her scheme is likely to be fraudulent.
Unreasonable Results
27. (a) Suppose you want to design a steam engine that has heat transfer to the environment at 270ºC and has a Carnot efficiency of 0.800. What temperature of hot steam must you use?
(b) What is unreasonable about the temperature?
(c) Which premise is unreasonable?
Unreasonable Results
28. Calculate the cold reservoir temperature of a steam engine that uses hot steam at \(450^{\circ} \mathrm{C}\) and has a Carnot efficiency of 0.700.
(b) What is unreasonable about the temperature?
(c) Which premise is unreasonable?
Solution
(a) –56.3ºC
(b) The temperature is too cold for the output of a steam engine (the local environment). It is below the freezing point of water.
(c) The assumed efficiency is too high.
9.11: Applications of Thermodynamics- Heat Pumps and Refrigerators
29. What is the coefficient of performance of an ideal heat pump that has heat transfer from a cold temperature of −25.0ºC to a hot temperature of 40.0ºC?
Answer
4.82
30. Suppose you have an ideal refrigerator that cools an environment at −20.0ºC and has heat transfer to another environment at 50.0ºC. What is its coefficient of performance?
31. What is the best coefficient of performance possible for a hypothetical refrigerator that could make liquid nitrogen at −200ºC and has heat transfer to the environment at 35.0ºC?
Answer
0.311
32. In a very mild winter climate, a heat pump has heat transfer from an environment at 5.00ºC to one at 35.0ºC. What is the best possible coefficient of performance for these temperatures? Explicitly show how you follow the steps in the Problem-Solving Strategies for Thermodynamics.
33. (a) What is the best coefficient of performance for a heat pump that has a hot reservoir temperature of 50.0ºC and a cold reservoir temperature of −20.0ºC?
(b) How much heat transfer occurs into the warm environment if \(3.60 \times 10^{7} \mathrm{~J}\) of work (\(10.0 \mathrm{~kW} \cdot \mathrm{h}\)) is put into it?
(c) If the cost of this work input is \(10.0 \text { cents } / \mathrm{kW} \cdot \mathrm{h}\), how does its cost compare with the direct heat transfer achieved by burning natural gas at a cost of 85.0 cents per therm. (A therm is a common unit of energy for natural gas and equals \(1.055 \times 10^{8} \mathrm{~J}\).)
Answer
(a) 4.61
(b) \(1.66 \times 10^{8} \mathrm{~J} \text { or } 3.97 \times 10^{4} \mathrm{kcal}\)
(c) To transfer \(1.66 \times 10^{8} \mathrm{~J}\), heat pump costs $1.00, natural gas costs $1.34.
34. (a) What is the best coefficient of performance for a refrigerator that cools an environment at −30.0ºC and has heat transfer to another environment at 45.0ºC?
(b) How much work in joules must be done for a heat transfer of 4186 kJ from the cold environment?
(c) What is the cost of doing this if the work costs 10.0 cents per \(3.60 \times 10^{6} \mathrm{~J}\) (a kilowatt-hour)?
(d) How many kJ of heat transfer occurs into the warm environment?
(e) Discuss what type of refrigerator might operate between these temperatures.
35. Suppose you want to operate an ideal refrigerator with a cold temperature of −10.0ºC, and you would like it to have a coefficient of performance of 7.00. What is the hot reservoir temperature for such a refrigerator?
Answer
27.6ºC
36. An ideal heat pump is being considered for use in heating an environment with a temperature of 22.0ºC. What is the cold reservoir temperature if the pump is to have a coefficient of performance of 12.0?
37. A 4-ton air conditioner removes \(5.06 \times 10^{7} \mathrm{~J}\) (48,000 British thermal units) from a cold environment in 1.00 h.
(a) What energy input in joules is necessary to do this if the air conditioner has an energy efficiency rating (\(\text { EER }\)) of 12.0?
(b) What is the cost of doing this if the work costs 10.0 cents per \(3.60 \times 10^{6} \mathrm{~J}\) (one kilowatt-hour)?
(c) Discuss whether this cost seems realistic. Note that the energy efficiency rating (\(\text { EER }\)) of an air conditioner or refrigerator is defined to be the number of British thermal units of heat transfer from a cold environment per hour divided by the watts of power input.
Answer
(a) 1.44×107 J
(b) 40 cents
(c) This cost seems quite realistic; it says that running an air conditioner all day would cost $9.59 (if it ran continuously).
38. Show that the coefficients of performance of refrigerators and heat pumps are related by \(C O P_{\text {ref }}=C O P_{\text {hp }}-1\).
39. Start with the definitions of the \(C O P\)s and the conservation of energy relationship between \(Q_{\mathrm{h}}\), \(Q_{\mathrm{c}}\), and \(W\).
9.13: Statistical Interpretation of Entropy and the Second Law of Thermodynamics- The Underlying Explanation
40. Using Table 9.13.3, verify the contention that if you toss 100 coins each second, you can expect to get 100 heads or 100 tails once in 2×1022 years; calculate the time to two-digit accuracy.
Solution
It should happen twice in every 1.27×1030 s or once in every 6.35×1029 s
\(\begin{array}{ll}
\left(6.35 \times 10^{29} \mathrm{~s}\right)\left(\frac{1 \mathrm{~h}}{3600 \mathrm{~s}}\right) \left(\frac{1 \mathrm{~d}}{24 \mathrm{~h}}\right)\left(\frac{1 \mathrm{y}}{365.25 \mathrm{~d}}\right) \\
= 2.0 \times 10^{22} \mathrm{y}
\end{array}\)
41. What percent of the time will you get something in the range from 60 heads and 40 tails through 40 heads and 60 tails when tossing 100 coins? The total number of microstates in that range is 1.22×1030. (Consult Table 9.13.3.)
42. (a) If tossing 100 coins, how many ways (microstates) are there to get the three most likely macrostates of 49 heads and 51 tails, 50 heads and 50 tails, and 51 heads and 49 tails?
(b) What percent of the total possibilities is this? (Consult Table 9.13.3.)
Solution
(a) 3.0×1029
(b) 24%
43. (a) What is the change in entropy if you start with 100 coins in the 45 heads and 55 tails macrostate, toss them, and get 51 heads and 49 tails?
(b) What if you get 75 heads and 25 tails?
(c) How much more likely is 51 heads and 49 tails than 75 heads and 25 tails?
(d) Does either outcome violate the second law of thermodynamics?
44. (a) What is the change in entropy if you start with 10 coins in the 5 heads and 5 tails macrostate, toss them, and get 2 heads and 8 tails?
(b) How much more likely is 5 heads and 5 tails than 2 heads and 8 tails? (Take the ratio of the number of microstates to find out.)
(c) If you were betting on 2 heads and 8 tails would you accept odds of 252 to 45? Explain why or why not.
Solution
(a) −2.38×10–23 J/K
(b) 5.6 times more likely
(c) If you were betting on two heads and 8 tails, the odds of breaking even are 252 to 45, so on average you would break even. So, no, you wouldn’t bet on odds of 252 to 45.
| Macrostate | Number of Microstates (W) | |
|---|---|---|
| Heads | Tails | |
| 10 | 0 | 1 |
| 9 | 1 | 10 |
| 8 | 2 | 45 |
| 7 | 3 | 120 |
| 6 | 4 | 210 |
| 5 | 5 | 252 |
| 4 | 6 | 210 |
| 3 | 7 | 120 |
| 2 | 8 | 45 |
| 1 | 9 | 10 |
| 0 | 10 | 1 |
45. (a) If you toss 10 coins, what percent of the time will you get the three most likely macrostates (6 heads and 4 tails, 5 heads and 5 tails, 4 heads and 6 tails)?
(b) You can realistically toss 10 coins and count the number of heads and tails about twice a minute. At that rate, how long will it take on average to get either 10 heads and 0 tails or 0 heads and 10 tails?
46. (a) Construct a table showing the macrostates and all of the individual microstates for tossing 6 coins. (Use Table \(\PageIndex{1}\) as a guide.)
(b) How many macrostates are there?
(c) What is the total number of microstates?
(d) What percent chance is there of tossing 5 heads and 1 tail?
(e) How much more likely are you to toss 3 heads and 3 tails than 5 heads and 1 tail? (Take the ratio of the number of microstates to find out.)
Solution
(b) 7
(c) 64
(d) 9.38%
(e) 3.33 times more likely (20 to 6)
47. In an air conditioner, 12.65 MJ of heat transfer occurs from a cold environment in 1.00 h.
(a) What mass of ice melting would involve the same heat transfer?
(b) How many hours of operation would be equivalent to melting 900 kg of ice?
(c) If ice costs 20 cents per kg, do you think the air conditioner could be operated more cheaply than by simply using ice? Describe in detail how you evaluate the relative costs.


