Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

1.14: Legendre Polynomials

Last updated

Mar 5, 2022
Save as PDF
- 1.13: Fitting a Least Squares Polynomial to a Set of Observational Points
- 1.15: Gaussian Quadrature - the Algorithm

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Consider the expression

$(1-2rx + r^2 ) ^{-1/2} , \label{1.14.1} \tag{1.14.1}$

in which $|x|$ and $|r|$ are both less than or equal to one. Expressions similar to this occur quite often in theoretical physics - for example in calculating the gravitational or electrostatic potentials of bodies of arbitrary shape. See, for example, Chapter 5, Sections 5.11 and 5.12.

Expand the expression $\ref{1.14.1}$ by the binomial theorem as a series of powers of $r$ . This is straightforward, though not particularly easy, and you might expect to spend several minutes in obtaining the coefficients of the first few powers of $r$ . You will find that the coefficient of $r^l$ is a polynomial expression in $x$ of degree $l$ . Indeed the expansion takes the form

$(1 - 2rx + r^2 )^{-1/2} = P_0 (x) + P_1 (x) r + P_2 (x) r^2 + P_3 (x) r^3 ... \label{1.14.2} \tag{1.14.2}$

The coefficients of the successive power of $r$ are the Legendre polynomials; the coefficient of $r^l$ , which is $P_l(x)$ , is the Legendre polynomial of order $l$ , and it is a polynomial in $x$ including terms as high as $x^l$ . We introduce these polynomials in this section because we shall need them in Section 1.15 on the derivation of Gaussian Quadrature.

If you have conscientiously tried to expand expression $\ref{1.14.1}$ , you will have found that

$P_0 (x) = 1, \quad P_1 (x) = x, \quad P_2 (x) = \frac{1}{2} (3x^2 - 1), \label{1.14.3} \tag{1.14.3}$

though you probably gave up with exhaustion after that and didn’t take it any further. If you look carefully at how you derived the first few polynomials, you may have discovered for yourself that you can obtain the next polynomial as a function of two earlier polynomials. You may even have discovered for yourself the following recursion relation:

$P_{l+1} = \frac{(2l+1)xP_l - lP_{l-1}}{l+1}. \label{1.14.4} \tag{1.14.4}$

This enables us very rapidly to obtain higher order Legendre polynomials, whether numerically or in algebraic form. For example, put $l = 1$ and show that Equation 1.12.4 results in $P_2 = \frac{1}{2} (3x^2 - 1)$ . You will then want to calculate $P_3$ , and then $P_4$ , and more and more and more. Another way to generate them is form the Equation

$P_{l+1} = \frac{1}{2^l l!} \frac{d^l}{dx^l} (x^2 - 1)^l . \label{1.14.5} \tag{1.14.5}$

Here are the first eleven Legendre polynomials:

$\begin{array}{l} P_0 = 1 \\ P_1 = x \\ P_2 = \frac{1}{2} (3x^2 - 1) \\ P_3 = \frac{1}{2} (5x^3 - 3x) \\ P_4 = \frac{1}{8} (35x^4 - 30x^2 + 3) \\ P_5 = \frac{1}{16} (63x^5 - 70x^3 + 15x) \\ P_6 = \frac{1}{16} (231x^6 - 315x^4 + 105x^2 - 5) \\ P_7 = \frac{1}{16} (429x^7 - 693x^5 + 315x^3 -35x) \\ P_8 = \frac{1}{128} (6435x^8 - 12012x^6 + 6930x^4 -1260x^2 + 35 \\ P_9 = \frac{1}{128} (12155x^9 - 25740x^7 + 18018x^5 - 4620x^3 + 315x) \\ P_{10} = \frac{1}{256} ( 46189 x^{10} - 109395x^8 + 90090x^6 - 30030x^4 + 3465x^2 - 63) \\ \label{1.14.6} \tag{1.14.6} \end{array}$

The polynomials with argument $\cos \theta$ are given in Section 5.11 of Chapter 5.

In what follows in the next section, we shall also want to know the roots of the Equations $P_l = 0$ for $l > 1$ . Inspection of the forms of these polynomials will quickly show that all odd polynomials have a root of zero, and all nonzero roots occur in positive/negative pairs. Having read Sections 1.4 and 1.5, we shall have no difficulty in finding the roots of these Equations. The roots $x_{l,i}$ are in the following table, which also lists certain coefficients $c_{l,i}$ , that will be explained in Section 1.15.

Roots of $P_l = 0$

$\begin{array}{c c c} l & x_{l,i} & c_{l,i} \\ \\ 2 & \pm 0.577 \ 350 \ 269 \ 190 & 1.000 \ 000 \ 000 \ 00 \\ \\ 3 & \pm 0.774 \ 596 \ 669 \ 241 & 0.555 \ 555 \ 555 \ 56 \\ & 0.000 \ 000 \ 000 \ 000 & 0.888 \ 888 \ 888 \ 89 \\ \\ 4 & \pm 0.861 \ 136 \ 311 \ 594 & 0.347 \ 854 \ 845 \ 14 \\ & \pm 0.339 \ 981 \ 043 \ 585 & 0.652 \ 145 \ 154 \ 86 \\ \\ 5 & \pm 0.906 \ 179 \ 845 \ 939 & 0.236 \ 926 \ 885 \ 06 \\ & \pm 0.538 \ 469 \ 310 \ 106 & 0.478 \ 628 \ 670 \ 50 \\ & 0.000 \ 000 \ 000 \ 000 & 0.568 \ 888 \ 888 \ 89 \\ \\ 6 & \pm 0.932 \ 469 \ 514 \ 203 & 0.171 \ 324 \ 492 \ 38 \\ & \pm 0.661 \ 209 \ 386 \ 466 & 0.360 \ 761 \ 573 \ 05 \\ & \pm 0.238 \ 619 \ 186 \ 083 & 0.467 \ 913 \ 934 \ 57 \\ \\ 7 & \pm 0.949 \ 107 \ 912 \ 343 & 0.129 \ 484 \ 966 \ 17 \\ & \pm 0.741 \ 531 \ 185 \ 599 & 0.279 \ 705 \ 391 \ 49 \\ & \pm 0.405 \ 845 \ 151 \ 377 & 0.381 \ 830 \ 050 \ 50 \\ & 0.000 \ 000 \ 000 \ 000 & 0.417 \ 959 \ 183 \ 68 \\ \\ 8 & \pm 0.960 \ 289 \ 856 \ 498 & 0.101 \ 228 \ 536 \ 29 \\ & \pm 0.796 \ 666 \ 477 \ 414 & 0.222 \ 381 \ 034 \ 45 \\ & \pm 0.525 \ 532 \ 409 \ 916 & 0.313 \ 706 \ 645 \ 88 \\ & \pm 0.183 \ 434 \ 642 \ 496 & 0.362 \ 683 \ 783 \ 38 \\ \\ 9 & \pm 0.968 \ 160 \ 239 \ 508 & 0.081 \ 274 \ 388 \ 36 \\ & \pm 0.836 \ 031 \ 107 \ 327 & 0.180 \ 648 \ 160 \ 69 \\ & \pm 0.613 \ 371 \ 432 \ 701 & 0.260 \ 610 \ 696 \ 40 \\ & \pm 0.324 \ 253 \ 423 \ 404 & 0.312 \ 347 \ 077 \ 04 \\ & 0.000 \ 000 \ 000 \ 000 & 0.330 \ 239 \ 355 \ 00 \\ \\ 10 & \pm 0.973 \ 906 \ 528 \ 517 & 0.066 \ 671 \ 343 \ 99 \\ & \pm 0.865 \ 063 \ 366 \ 689 & 0.149 \ 451 \ 349 \ 64 \\ & \pm 0.679 \ 409 \ 568 \ 299 & 0.219 \ 086 \ 362 \ 24 \\ & \pm 0.433 \ 395 \ 394 \ 129 & 0.269 \ 266 \ 719 \ 47 \\ & \pm 0.148 \ 874 \ 338 \ 982 & 0.295 \ 524 \ 224 \ 66 \\ \\ 11 & \pm 0.978 \ 228 \ 658 \ 146 & 0.055 \ 668 \ 567 \ 12 \\ & \pm 0.887 \ 062 \ 599 \ 768 & 0.125 \ 580 \ 369 \ 46 \\ & \pm 0.730 \ 152 \ 005 \ 574 & 0.186 \ 290 \ 210 \ 93 \\ & \pm 0.519 \ 096 \ 129 \ 207 & 0.233 \ 193 \ 764 \ 59 \\ & \pm 0.269 \ 543 \ 155 \ 952 & 0.262 \ 804 \ 544 \ 51 \\ & 0.000 \ 000 \ 000 \ 000 & 0.272 \ 925 \ 086 \ 78 \\ \\ 12 & \pm 0.981 \ 560 \ 634 \ 247 & 0.047 \ 175 \ 336 \ 39 \\ & \pm 0.904 \ 117 \ 256 \ 370 & 0.106 \ 939 \ 325 \ 99 \\ & \pm 0.769 \ 902 \ 674 \ 194 & 0.160 \ 078 \ 328 \ 54 \\ & \pm 0.587 \ 317 \ 954 \ 287 & 0.203 \ 167 \ 426 \ 72 \\ & \pm 0.367 \ 831 \ 498 \ 998 & 0.233 \ 492 \ 536 \ 54 \\ & \pm 0.125 \ 233 \ 408 \ 511 & 0.249 \ 147 \ 045 \ 81 \\ \\ 13 & \pm 0.984 \ 183 \ 054 \ 719 & 0.040 \ 484 \ 004 \ 77 \\ & \pm 0.917 \ 598 \ 399 \ 223 & 0.092 \ 121 \ 499 \ 84 \\ & \pm 0.801 \ 578 \ 090 \ 733 & 0.138 \ 873 \ 510 \ 22 \\ & \pm 0.642 \ 349 \ 339 \ 440 & 0.178 \ 145 \ 980 \ 76 \\ & \pm 0.448 \ 492 \ 751 \ 036 & 0.207 \ 816 \ 047 \ 54 \\ & \pm 0.230 \ 458 \ 315 \ 955 & 0.226 \ 283 \ 180 \ 26 \\ & 0.000 \ 000 \ 000 \ 000 & 0.232 \ 551 \ 553 \ 23 \\ \\ 14 & \pm 0.986 \ 283 \ 808 \ 697 & 0.035 \ 119 \ 460 \ 33 \\ & \pm 0.928 \ 434 \ 883 \ 664 & 0.080 \ 158 \ 087 \ 16 \\ & \pm 0.827 \ 201 \ 315 \ 070 & 0.121 \ 518 \ 570 \ 69 \\ & \pm 0.687 \ 292 \ 904 \ 812 & 0.157 \ 203 \ 167 \ 16 \\ & \pm 0.515 \ 248 \ 636 \ 358 & 0.185 \ 538 \ 397 \ 48 \\ & \pm 0.319 \ 112 \ 368 \ 928 & 0.205 \ 198 \ 463 \ 72 \\ & \pm 0.108 \ 054 \ 948 \ 707 & 0.215 \ 263 \ 853 \ 46 \\ \\ 15 & \pm 0.987 \ 992 \ 518 \ 020 & 0.030 \ 753 \ 242 \ 00 \\ & \pm 0.937 \ 273 \ 392 \ 401 & 0.070 \ 366 \ 047 \ 49 \\ & \pm 0.848 \ 206 \ 583 \ 410 & 0.107 \ 159 \ 220 \ 47 \\ & \pm 0.724 \ 417 \ 731 \ 360 & 0.139 \ 570 \ 677 \ 93 \\ & \pm 0.570 \ 972 \ 172 \ 609 & 0.166 \ 269 \ 205 \ 82 \\ & \pm 0.394 \ 151 \ 347 \ 078 & 0.186 \ 161 \ 000 \ 02 \\ & \pm 0.201 \ 194 \ 093 \ 997 & 0.198 \ 431 \ 485 \ 33 \\ & 0.000 \ 000 \ 000 \ 000 & 0.202 \ 578 \ 241 \ 92 \\ \\ 16 & \pm 0.989 \ 400 \ 934 \ 992 & 0.027 \ 152 \ 459 \ 41 \\ & \pm 0.944 \ 575 \ 023 \ 073 & 0.062 \ 253 \ 523 \ 94 \\ & \pm 0.865 \ 631 \ 202 \ 388 & 0.095 \ 158 \ 511 \ 68 \\ & \pm 0.755 \ 404 \ 408 \ 355 & 0.124 \ 628 \ 971 \ 26 \\ & \pm 0.617 \ 876 \ 244 \ 403 & 0.149 \ 595 \ 988 \ 82 \\ & \pm 0.458 \ 016 \ 777 \ 657 & 0.169 \ 156 \ 519 \ 39 \\ & \pm 0.281 \ 603 \ 550 \ 779 & 0.182 \ 603 \ 415 \ 04 \\ & \pm 0.095 \ 012 \ 509 \ 838 & 0.189 \ 450 \ 610 \ 46 \\ \\ 17 & \pm 0.990 \ 575 \ 475 \ 315 & 0.024 \ 148 \ 302 \ 87 \\ & \pm 0.950 \ 675 \ 521 \ 769 & 0.055 \ 459 \ 529 \ 38 \\ & \pm 0.880 \ 239 \ 153 \ 727 & 0.085 \ 036 \ 148 \ 32 \\ & \pm 0.781 \ 514 \ 003 \ 897 & 0.111 \ 883 \ 847 \ 19 \\ & \pm 0.657 \ 671 \ 159 \ 217 & 0.135 \ 136 \ 368 \ 47 \\ & \pm 0.512 \ 690 \ 537 \ 086 & 0.154 \ 045 \ 761 \ 08 \\ & \pm 0.351 \ 231 \ 763 \ 454 & 0.168 \ 004 \ 102 \ 16 \\ & \pm 0.178 \ 484 \ 181 \ 496 & 0.176 \ 562 \ 705 \ 37 \\ & 0.000 \ 000 \ 000 \ 000 & 0.179 \ 446 \ 470 \ 35 \\ \end{array}$

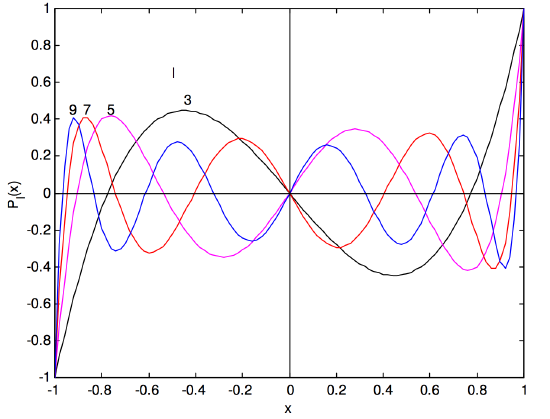
For interest, I draw graphs of the Legendre polynomials in figures $\text{I.7}$ and $\text{I.8}$ .

Figure $\text{I.7}$ . Legendre polynomials for even $\text{I}$
alt

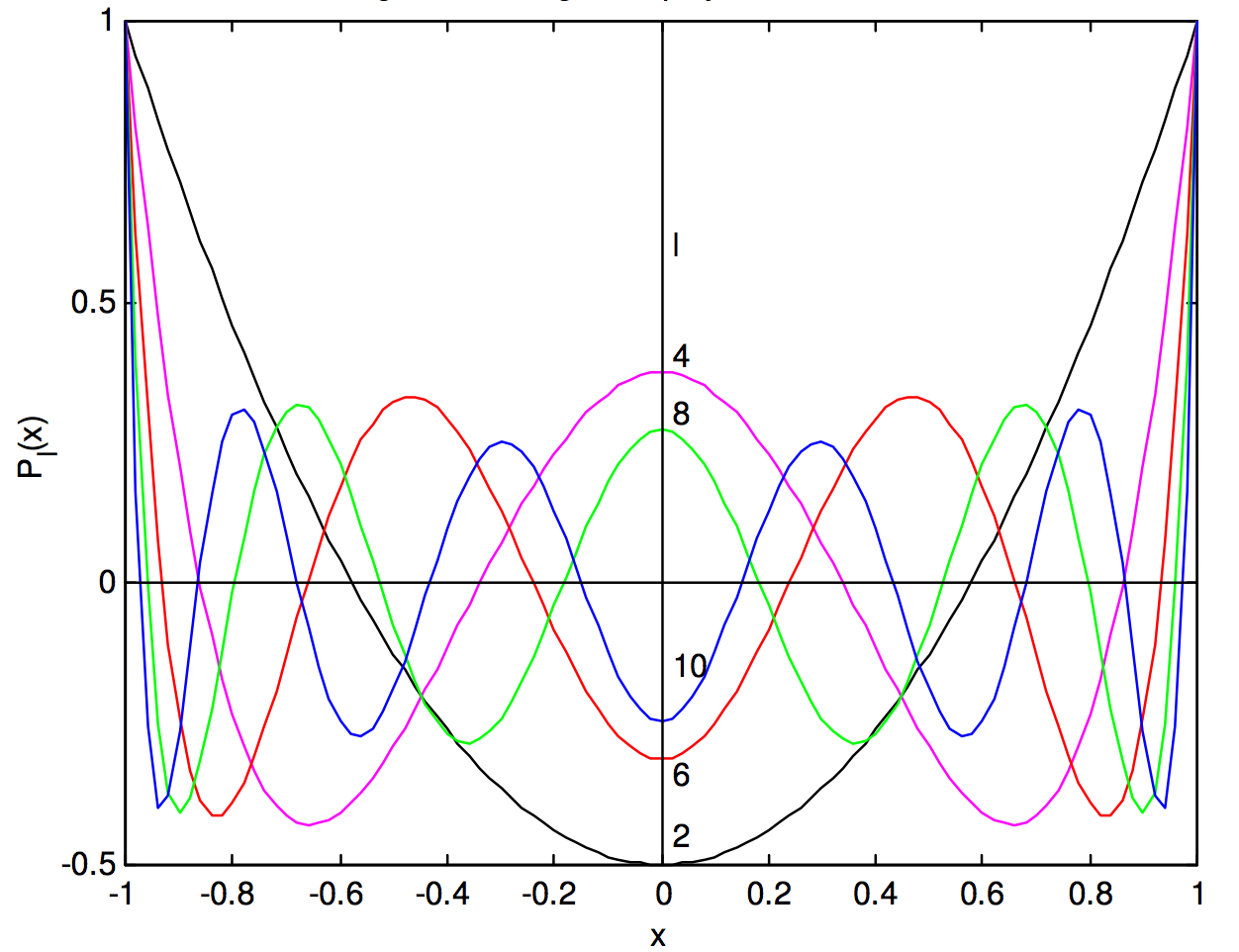
Figure $\text{I.8}$ . Legendre polynomials for odd $\text{I}$
alt

For further interest, it should be easy to verify, by substitution, that the Legendre polynomials are solutions of the differential Equation

$(1-x^2)y^{\prime \prime} - 2xy^\prime + l(l+1) y = 0. \label{1.14.7} \tag{1.14.7}$

The Legendre polynomials are solutions of this and related Equations that appear in the study of the vibrations of a solid sphere (spherical harmonics) and in the solution of the Schrödinger Equation for hydrogen-like atoms, and they play a large role in quantum mechanics.

Support Center

How can we help?