15.7: Two-Dimensional Collisions in Center-of-Mass Reference Frame
( \newcommand{\kernel}{\mathrm{null}\,}\)
Two-Dimensional Collision in Center-of-Mass Reference Frame
Consider the elastic collision between two particles in the laboratory reference frame (Figure 15.9). Particle 1 of mass m1 is initially moving with velocity →v1,i and elastically collides with a particle 2 of mass m2 that is initially at rest. After the collision, the particle 1 moves with velocity →v1,f and particle 2 moves with velocity →v2,f. In section 15.7.1 we determined how to find v1,f, v2,f, and θ2,f in terms of v1,i and θ2,f. We shall now analyze the collision in the center-of-mass reference frame, which is boosted form the laboratory frame by the velocity of center-of-mass given by →vcm=m1→v1,im1+m2
Because we assumed that there are no external forces acting on the system, the center-of-mass velocity remains constant during the interaction.
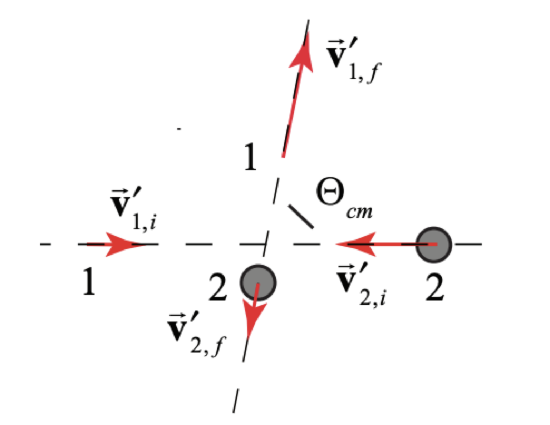
Recall the velocities of particles 1 and 2 in the center-of-mass frame are given by (Equation,(15.2.9) and (15.2.10)). In the center-of-mass reference frame the velocities of the two incoming particles are in opposite directions, as are the velocities of the two outgoing particles after the collision (Figure 15.13). The angle Θcm between the incoming and outgoing velocities is called the center-of-mass scattering angle.
Scattering in the Center-of-Mass Reference Frame
Consider a collision between particle 1 of mass m1 and velocity →v1,i and particle 2 of mass m2 at rest in the laboratory frame. Particle 1 is scattered elastically through a scattering angle Θ in the center-of-mass frame. The center-of-mass velocity is given by →vcm=m1→v1,im1+m2
In the center-of-mass frame, the momentum of the system of two particles is zero →0=m1→v′1,i+m2→v′2,i=m1→v′1,f+m2→v′2,f Therefore →v′1,i=−m2m1→v′2,i →v′1,f=−m2m1→v′2,f The energy condition in the center-of-mass frame is 12m1v′21,i+12m2v′22,i=12m1v′21,f+12m2v′22,f Substituting Equations (15.7.4) and (15.7.5) into Equation (15.7.6) yields v′1,i=v′1,f (we are only considering magnitudes). Therefore v′2,i=v′2,f Because the magnitude of the velocity of a particle in the center-of-mass reference frame is proportional to the relative velocity of the two particles, Equations (15.7.7) and (15.7.8) imply that the magnitude of the relative velocity also does not change |→v′1,2,i|=|→v′1,2,f| verifying our earlier result that for an elastic collision the relative speed remains the same, (Equation (15.2.20)). However the direction of the relative velocity is rotated by the center-of-mass scattering angle Θcm. This generalizes the energy-momentum principle to two dimensions. Recall that the relative velocity is independent of the reference frame, →v1,i−→v2,i=→v′1,i−→v′2,i In the laboratory reference frame →v2,i=→0, hence the initial relative velocity is →v′1,2,i=→v1,2,i=→v1,i, and the velocities in the center-of-mass frame of the particles are then →V′1,i=μm1→v1,i →v′2,i=−μm2→v1,i Therefore the magnitudes of the final velocities in the center-of-mass frame are v′1,f=v′1,i=μm1v′1,2,i=μm1v1,2,i=μm1v1,i v′2,f=v′2,i=μm2v′1,2,i=μm2v1,2,i=μm2v1,i
Example 15.8 Scattering in the Lab and CM Frames
Particle 1 of mass m1 and velocity →v1,i by a particle of mass m2 at rest in the laboratory frame is scattered elastically through a scattering angle Θ in the center of mass frame, (Figure 15.14). Find (i) the scattering angle of the incoming particle in the laboratory frame, (ii) the magnitude of the final velocity of the incoming particle in the laboratory reference frame, and (iii) the fractional loss of kinetic energy of the incoming particle.
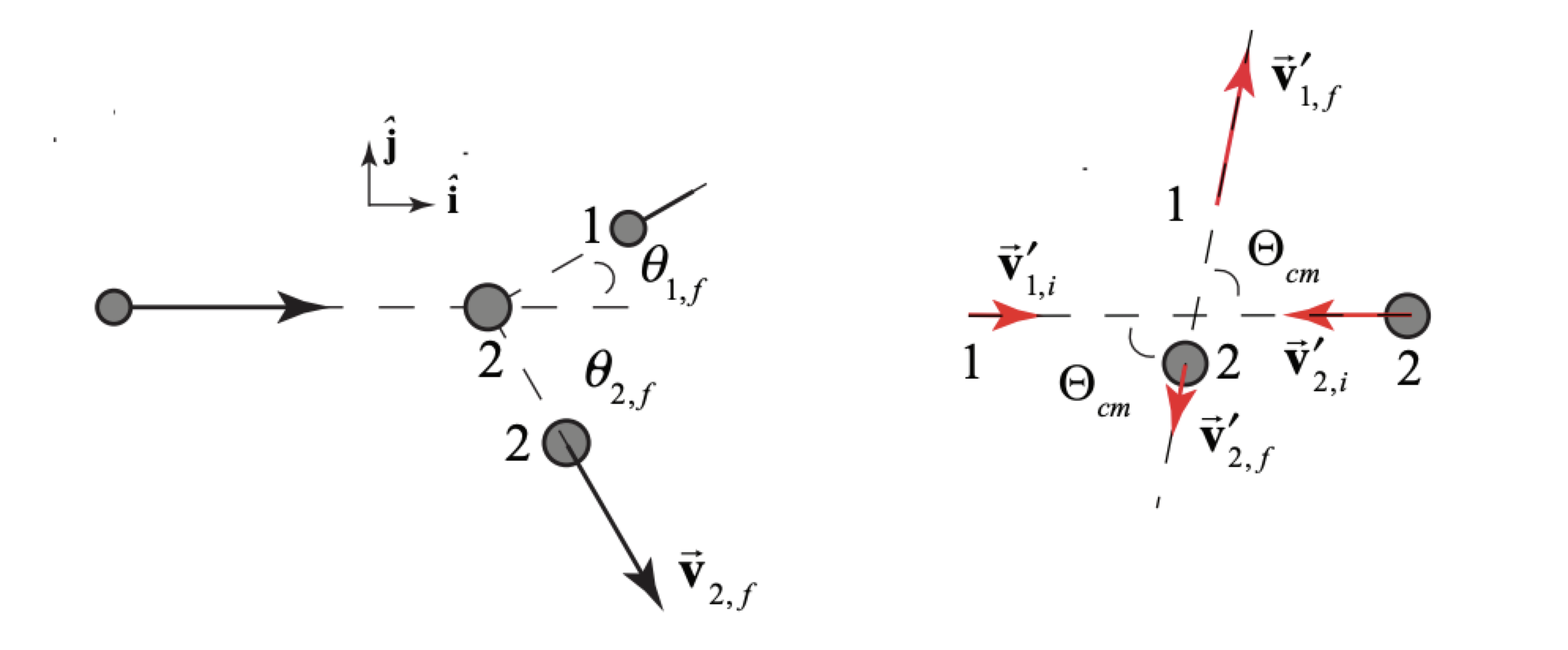
Solution
i) In order to determine the center-of-mass scattering angle we use the transformation law for velocities →v′1,f=→v1,f−→vcm In Figure 15.15 we show the collision in the center-of-mass frame along with the laboratory frame final velocities and scattering angles.
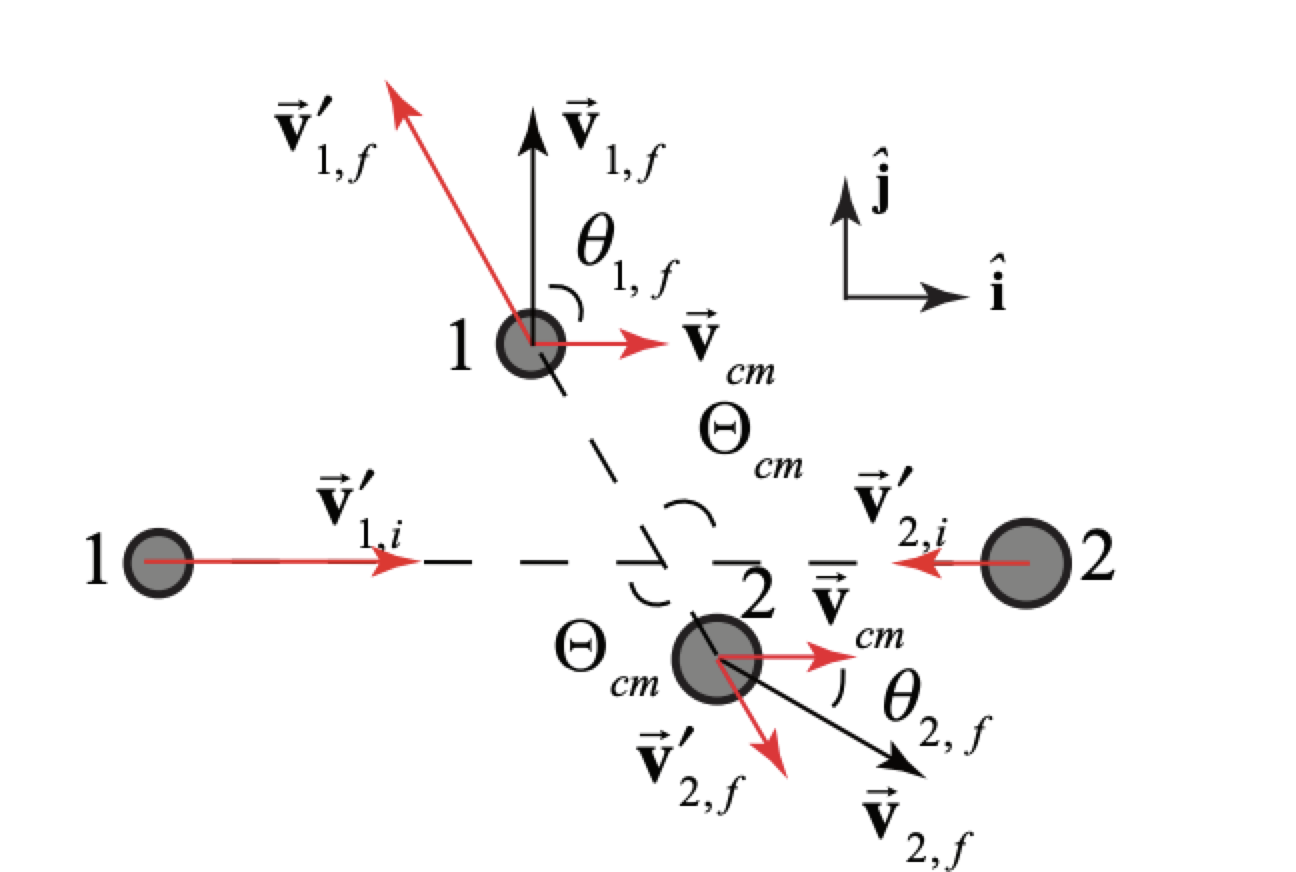
Vector decomposition of Equation (15.7.15) yields v1,fcosθ1,i=v′1,fcosΘcm−vcm v1,fsinθ1,i=v′1,fsinΘcm where we choose as our directions the horizontal and vertical Divide Equation (15.7.17) by (15.7.16) yields tanθ1,i=v1,fsinθ1,iv1,fcosθ1,i=v′1,fsinΘcmv′1,fcosΘcm−vcm Because v′1,i=v′1,f, we can rewrite Equation (15.7.18) as tanθ1,i=v′1,isinΘcmv′1,icosΘcm−vcm
We now substitute Equations (15.7.12) and vcm=m1v1,i/(m1+m2) into Equation (15.7.19) yielding tanθ1,i=m2sinΘcmcosΘcm−m1/m2 Thus in the laboratory frame particle 1 scatters by an angle θ1,i=tan−1(m2sinΘcmcosΘcm−m1/m2)
ii) We can calculate the square of the final velocity in the laboratory frame →v1,f⋅→v1,f=(→v′1,f+→vcm)⋅(→v′1,f+→vcm) which becomes v21,f=v′21,f+2→v′1,f⋅→vcm+v2cm=v′21,f+2v′1,fvcmcosΘcm+v2cm
We use the fact that v′1,f=v′1,i=(μ/m1)v1,2,i=(μ/m1)v1,i=(m2/m1+m2)v1,i to rewrite Equation (15.7.23) as v21,f=(m2m1+m2)2v21,i+2m2m1(m1+m2)2v1,icosΘcm+m21(m1+m2)2v21,i Thus v1,f=(m22+2m2m1cosΘcm+m21)1/2m1+m2v1,i
(iii) The fractional change in the kinetic energy of particle 1 in the laboratory frame is given by K1,f−K1,iK1,i=v21,f−v21,iv21,i=m22+2m2m1cosΘcm+m21(m1+m2)2−1=2m2m1(cosΘcm−1)(m1+m2)2 We can also determine the scattering angle Θcm in the center-of-mass reference frame from the scattering angle θ1,i of particle 1 in the laboratory. We now rewrite the momentum relations as v1,fcosθ1,i+vcm=v′1,fcosΘcm v1,fsinθ1,i=v′1,fsinΘcm
In a similar fashion to the above argument, we have that tanΘcm=v1,fsinθ1,fv1,fcosθ1,f+vcm Recall from our analysis of the collision in the laboratory frame that if we specify one of the four parameters v1,f,v2,f,θ1,f or v1,f then we can solve for the other three in terms of the initial parameters v1,i and v2,i. With that caveat, we can use Equation (15.7.29) to determine Θcm


