5.4: Fluctuations of the Vacuum
( \newcommand{\kernel}{\mathrm{null}\,}\)
The great problem is in understanding the meaning of virtual particles. Suppose we are studying the vacuum state in QED. We wish to describe this vacuum in terms of the states of no positrons, electrons and photons (the naive vacuum). Since these particles interact we have short-lived states where e+e− pairs, and photons, and .... appear for a short while and disappear again. This is also true for real particles: a real electron is a “bare” electron surrounded by a cloud of virtual photons, e+e− pairs, etc. A photon can be an e+e− pair part of the time, and more of such anomalies.
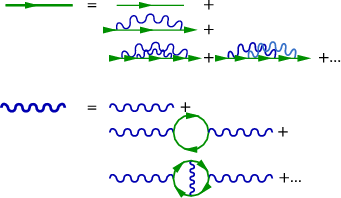
Feynman Diagrams
As I have sketched above, Feynman diagrams can be used to describe what is happening in these processes. These describe the matrix elements, and the actual transition probability is proportional to the square of this matrix elements. One can show that each electron-photon coupling vertex is proportional to e, and thus in the square each vertex gives a factor e2. Actually by drawing time in the vertical direction and space in the horizontal (schematically, of course), we see that the the two possible couplings of the photon to matter – Bremsstrahlung and pair creation are one and the same process. Still it helps to distinguish. Note that at each vertex charge is conserved as well as momentum!
This can actually be combined into a dimensionless quantity
α=e24πϵ0ℏc≈1137.
We should expand in α rather than e2 since expansion parameters, being “unphysical” can not have dimensions. In other words in order to carry through this mathematical concept the natural scale of a diagram is set by the power of α it carries. Due to the smallness of α we normally consider only the diagrams with as few vertices as possible. Let me list the two diagrams for electron-positron scattering, both proportional to α2, as given in Figure 5.4.2.
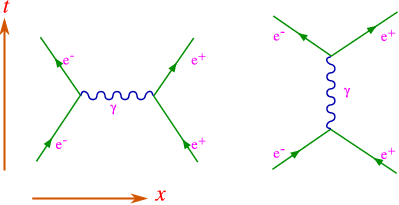
Why is there only one such diagram for e−e− scattering? Charge conservation.
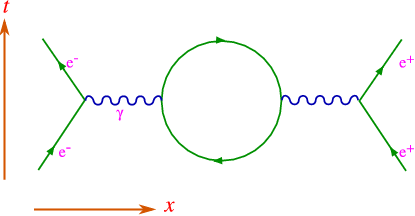
We can also construct higher order diagrams, as in Figure 5.4.3.
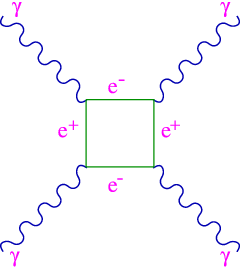
We can also calculate the scattering of light by light, which only comes in at α4, see Figure 5.4.4.
The sum of all diagrams contributing to a given process is called the perturbation series.


