13.13: Schrödinger's Cat

Radioactive Decay

Some elements are unstable, decaying via the weak interaction into other elements. Such substances are called radioactive. For example, Nitrogen-13 decays into Carbon-13 plus an electron plus an anti-neutrino.

There are two factors that determine that rate at which a sample of radioactive atoms decays:

1. How many atoms are there? Twice as many atoms will have a total decay rate that is double.
2. What is the tendency of a particular atom to decay.

The tendency of an element to decay is expressed by its half-life.

The half-life of Nitrogen-13 is almost exactly 10 minutes. What this number means is that if we have a large "pot" of Nitrogen-13 and wait 10 minutes one half of the Nitrogen-13 atoms will have decayed and one half will not have decayed. If we wait a further 10 minutes one half of the remaining sample of atoms will have decayed and one half will not. After a further 10 minutes one half of that remaining sample will have decayed.

The concept of half-live is sort of reminiscent of a famous paradox by Xeno, who argued that we can never walk out of a room. If we head towards the door, eventually we get half way towards it. If we keep walking we will have gotten half way through the remaining distance to the door. And then if we keep walking we get half way through that remaining distance. So we keep getting half way towards the door and never actually get there.

Here are some half-lives:

Atom	Half-Life
protons	> 10^32 years (i.e. consistent with being stable
Carbon-14	5,730 years
Cobalt-60	1,925 days
Nitrogen-13	10 minutes

You may access a Flash animation of 500 radioactive atoms of the fictitious element Balonuim by clicking here.

For radioactive substances, one crucial factor in discussing the half-life is that we were discussing a large collection of atoms. What if we only have two such Nitrogen-13 atoms? Then if we wait 10 minutes, one-half life, there is a 50% chance that one of the atoms will have decayed. So this is sort of similar to flipping two coins. Whether a particular coin comes up heads is about a 50% chance. For flipping two coins we can get both heads, one head and one tail, or both tails. Similarly for two radioactive atoms we could end up with both decaying, one decaying and the other not, or both not decaying.

Imagine that after 10 minutes the atom on the right decayed and the one on the left did not decay.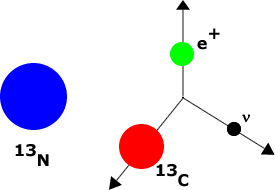

We ask a basic question: What is the difference between the two Nitrogen-13 atoms?

The answer to this is trivially easy: one atom decayed and the other did not.

A more interesting question is: What was the difference between the two Nitrogen-13 atoms before we waited 10 minutes?

The answer to this better question is sort of hard. According to Quantum Mechanics there was no difference between the two atoms: we had two completely identical atoms but one decayed and the other did not.

Einstein never accepted Quantum Mechanics, and this part of the theory is one of the reasons. He summarised his objections by saying "God does not play at dice with the universe." Bohr responded "Quit telling God what to do!"

Einstein's God may not play at dice, but there are other views of divinity. For example, in the Bhagavad Gita Krishna says:

"I am the game of dice. I am the self centered in the heart of all beings."

If, with Einstein, we reject the idea that completely identical initial states can evolve to different outcomes, then we conclude that initially there must have been some difference, some variable, that distinguishes the two Nitrogen-13 atoms. To date all attempts to discover what that variable is have failed; thus we would say that there is some hidden variable inside the atoms. In Quantum Mechanics there are no such variables.

The Cat Paradox

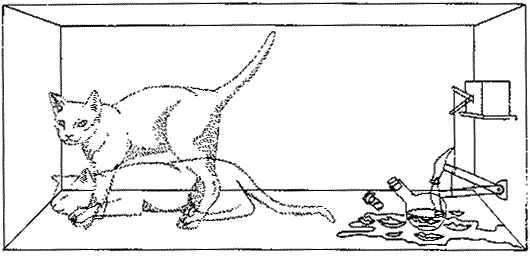
In the early 1930's Erwin Schrödinger published a way of thinking about the circumstance of radioactive decay that is still useful. We imagine an apparatus containing just one Nitrogen-13 atom and a detector that will respond when the atom decays. Connected to the detector is a relay connected to a hammer, and when the atom decays the relay releases the hammer which then falls on a glass vial containing poison gas. We take the entire apparatus and put it in a box. We also place a cat in the box, close the lid, and wait 10 minutes.

We then ask: Is the cat alive or dead? The answer according to quantum mechanics is that it is 50% dead and 50% alive.

Quantum Mechanics describes the world in terms of a wave function. DeWitt wrote about the cat that "at the end of [one half-life] the total wave function for the system will have a form in which the living cat and dead cat are mixed in equal portions." (Reference: B.S. DeWitt and N. Graham, eds., The Many-Worlds Interpretation of Quantum Mechanics (Princeton, 1973), pg. 156.)

When we open the box, we "collapse the wave function" or "collapse the state" and have either a live cat or a dead cat.

Of course, this is just a thought experiment. So far as I know nobody has actually every done this experiment.

In a sense the cat is a "red herring" [sorry!]. The paradox is just an illuminating way of thinking about the consequences of radioactive decay being totally random.

Imagine we have a friend waiting outside when we open the box. For us the wave function collapses and we have, say, a live cat. But our friend's wave function does not collapse until he comes into the room. This leads to a strong solipsism, since our friend can they say that we owe our objective existence to his kind intervention in coming into the room and collapsing our state.

As Heisenberg said, then, "The wave function represents partly a fact and partly our knowledge of a fact."

Our friend needn't have come into the room to collapse his wave function: if we have a cell phone we can call him and tell him the result of the experiment. Of course, this assumes that we don't lie to him and tell him the cat is dead when it is alive.

Unexplained but apparently true is the fact that when a state collapses, it collapses into the same state for everybody. If we see a live cat everybody sees a live cat (unless they or us are hallucinating).

As de Beauregard commented: "Finally, the need for consistency of the whole scheme leads me to think of the world we are living in as a Leibnitzian world, where cats are rather high in the hierarchy of monads." Reference: Foundations of Physics 6, 539 (1976).

Paradoxes of Quantum Mechanics

There are two major paradoxes of Quantum Mechanics, each illustrating different aspects of the quantum mystery. Schrödinger's Cat is one of them, and the other is the Double Slit. Notes on the double slit may be accessed either in html or pdf by clicking on the links to the left.

Each paradox shows different aspects of the "collapse of the state."

Double Slit

Shows that the collapse of the state is real, irreversible, and causes a qualitative change in the later time evolution of the system.

Schrödingers Cat

Shows that our consciousness and knowledge are somehow mixed up in this process.

Tags recommended by the template: article:topic

Author

David M. Harrison, Department of Physics, University of Toronto, [e-mail].