8.3: Orbital Magnetic Dipole Moment of the Electron
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain why the hydrogen atom has magnetic properties
- Explain why the energy levels of a hydrogen atom associated with orbital angular momentum are split by an external magnetic field
- Use quantum numbers to calculate the magnitude and direction of the orbital magnetic dipole moment of a hydrogen atom
In Bohr’s model of the hydrogen atom, the electron moves in a circular orbit around the proton. The electron passes by a particular point on the loop in a certain time, so we can calculate a current I=Q/t. An electron that orbits a proton in a hydrogen atom is therefore analogous to current flowing through a circular wire (Figure 8.3.1). In the study of magnetism, we saw that a current-carrying wire produces magnetic fields. It is therefore reasonable to conclude that the hydrogen atom produces a magnetic field and interacts with other magnetic fields.
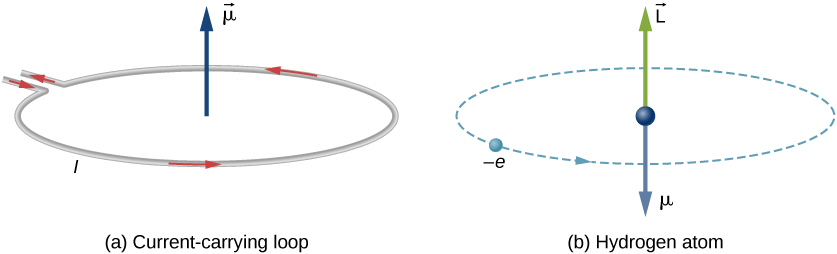
The orbital magnetic dipole moment is a measure of the strength of the magnetic field produced by the orbital angular momentum of an electron. From Force and Torque on a Current Loop, the magnitude of the orbital magnetic dipole moment for a current loop is
μ=IA,
where I is the current and A is the area of the loop. (For brevity, we refer to this as the magnetic moment.) The current I associated with an electron in orbit about a proton in a hydrogen atom is
I=eT,
where e is the magnitude of the electron charge and T is its orbital period. If we assume that the electron travels in a perfectly circular orbit, the orbital period is
T=2πrv,
where r is the radius of the orbit and v is the speed of the electron in its orbit. Given that the area of a circle is πr2, the absolute magnetic moment is
μ=IA=e(2πrv)πr2=evr2.
It is helpful to express the magnetic momentum μμ in terms of the orbital angular momentum (→L=→r×→p). Because the electron orbits in a circle, the position vector →r and the momentum vector →p form a right angle. Thus, the magnitude of the orbital angular momentum is
L=|→L|=|→r×→p|=rpsinθ=rmv.
Combining these two equations, we have
μ=(e2me)L.
In full vector form, this expression is written as
→μ=−(e2me)→L.
The negative sign appears because the electron has a negative charge. Notice that the direction of the magnetic moment of the electron is antiparallel to the orbital angular momentum, as shown in Figure 8.3.1b. In the Bohr model of the atom, the relationship between →μ and →L in Equation ??? is independent of the radius of the orbit.
The magnetic moment μ can also be expressed in terms of the orbital angular quantum number l. Combining Equation ??? and Equation ???, the magnitude of the magnetic moment is
μ=(e2me)L=(e2me)√l(l+1)ℏ=μB√l(l+1).
The z-component of the magnetic moment is
μz=−(e2me)Lz=−(e2me)mℏ=−μBm.
The quantity μB is a fundamental unit of magnetism called the Bohr magneton, which has the value 9.3×10−24Joule/Tesla (J/T) or 5.8×10−5eV/T. Quantization of the magnetic moment is the result of quantization of the orbital angular momentum.
As we will see in the next section, the total magnetic dipole moment of the hydrogen atom is due to both the orbital motion of the electron and its intrinsic spin. For now, we ignore the effect of electron spin.
What is the magnitude of the orbital dipole magnetic moment μ of an electron in the hydrogen atom in the (a) s state, (b) p state, and (c) d state? (Assume that the spin of the electron is zero.)
Strategy
The magnetic momentum of the electron is related to its orbital angular momentum L. For the hydrogen atom, this quantity is related to the orbital angular quantum number l. The states are given in spectroscopic notation, which relates a letter (s, p, d, etc.) to a quantum number.
Solution
The magnitude of the magnetic moment is given in Equation ???:
μz=−(e2me)L=(e2me)√l(l+1)ℏ=μB√l(l+1).
- For the s state, l=0 so we have μ=0 and μz=0.
- For the p state, l=1 and we have μ=μB√1(1+1)=√2μB μz=−μBm where m=(−1,0,1) so μz=μB,0,−μB.
- For the d state, l=2 and we obtain μ=μB√2(2+1)=√6μB μz=−μBm where m=(−2,−1,0,1,2) so μz=2μB,μB0,−μB−2μB.
Significance
In the s state, there is no orbital angular momentum and therefore no magnetic moment. This does not mean that the electron is at rest, just that the overall motion of the electron does not produce a magnetic field. In the p state, the electron has a magnetic moment with three possible values for the z-component of this magnetic moment; this means that magnetic moment can point in three different polar directions—each antiparallel to the orbital angular momentum vector. In the d state, the electron has a magnetic moment with five possible values for the z-component of this magnetic moment. In this case, the magnetic moment can point in five different polar directions.
A hydrogen atom has a magnetic field, so we expect the hydrogen atom to interact with an external magnetic field—such as the push and pull between two bar magnets. From Force and Torque on a Current Loop, we know that when a current loop interacts with an external magnetic field →B, it experiences a torque given by
→τ=I(→A×→B)=→μ×→B,
where I is the current, →A is the area of the loop, →μ is the magnetic moment, and →B is the external magnetic field. This torque acts to rotate the magnetic moment vector of the hydrogen atom to align with the external magnetic field. Because mechanical work is done by the external magnetic field on the hydrogen atom, we can talk about energy transformations in the atom. The potential energy of the hydrogen atom associated with this magnetic interaction is given by Equation ???:
U=−→μ⋅→B.
If the magnetic moment is antiparallel to the external magnetic field, the potential energy is large, but if the magnetic moment is parallel to the field, the potential energy is small. Work done on the hydrogen atom to rotate the atom’s magnetic moment vector in the direction of the external magnetic field is therefore associated with a drop in potential energy. The energy of the system is conserved, however, because a drop in potential energy produces radiation (the emission of a photon). These energy transitions are quantized because the magnetic moment can point in only certain directions.
If the external magnetic field points in the positive z-direction, the potential energy associated with the orbital magnetic dipole moment is
U(θ)=−μBcosθ=−μzB=−(−μBm)=mμBB,
where μB is the Bohr magneton and m is the angular momentum projection quantum number (or magnetic orbital quantum number), which has the values
m=−l,−l+1,...,0,...,l−1,l.
For example, in the l=1 electron state, the total energy of the electron is split into three distinct energy levels corresponding to U=−μBB,0,μBB.
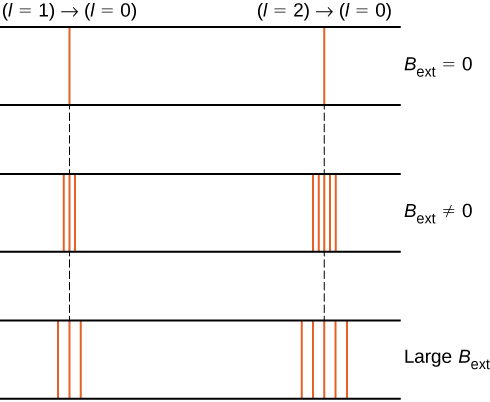
The splitting of energy levels by an external magnetic field is called the Zeeman effect. Ignoring the effects of electron spin, transitions from the l=1 state to a common lower energy state produce three closely spaced spectral lines (Figure 8.3.2, left column). Likewise, transitions from the l=2 state produce five closely spaced spectral lines (right column). The separation of these lines is proportional to the strength of the external magnetic field. This effect has many applications. For example, the splitting of lines in the hydrogen spectrum of the Sun is used to determine the strength of the Sun’s magnetic field. Many such magnetic field measurements can be used to make a map of the magnetic activity at the Sun’s surface called a magnetogram (Figure 8.3.3).



