11.1: Math Tutorial — Cross Product

Last updated
Save as PDF

Page ID: 32989

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

There are two ways to multiply two vectors together, the dot product and the cross product. We have already studied the dot product of two vectors, which results in a scalar or single number.

Figure 11.1: Illustration of the cross product of two vectors A and B. The resulting vector C is perpendicular to the plane defined by A and B.

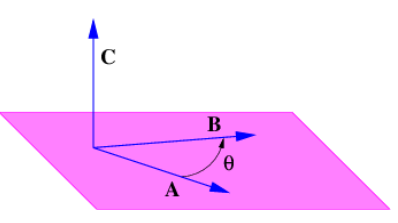
The cross product of two vectors results in a third vector, and is written symbolically as follows:

\[\mathbf{C}=\mathbf{A} \times \mathbf{B}\label{11.1}\]

As illustrated in figure 11.1, the cross product of two vectors is perpendicular to the plane defined by these vectors. However, this doesn’t tell us whether the resulting vector in figure 11.1 points upward out of the plane or downward. This ambiguity is resolved using the right-hand rule:

Point the uncurled fingers of your right hand along the direction of the first vector A.
Rotate your arm until you can curl your fingers in the direction of the second vector B.
Your stretched out thumb now points in the direction of the cross product vector C

The magnitude of the cross product is given by

\[|\mathbf{C}|=|\mathbf{A}||\mathbf{B}| \sin (\theta)\label{11.2}\]

where |A| and |B| are the magnitudes of A and B, and θ is the angle between these two vectors. Note that the magnitude of the cross product is zero when the vectors are parallel or anti-parallel, and maximum when they are perpendicular. This contrasts with the dot product, which is maximum for parallel vectors and zero for perpendicular vectors.

Notice that the cross product does not commute, i. e., the order of the vectors is important. In particular, it is easy to show using the right-hand rule that

\[\mathbf{A} \times \mathbf{B}=-\mathbf{B} \times \mathbf{A}\label{11.3}\]

An alternate way to compute the cross product is most useful when the two vectors are expressed in terms of components, i. e., \(A=\left(A_{x}, A_{y} \cdot A_{z}\right) \text { and } B=\left(B_{x}, B_{y}, B_{z}\right)\)

\[\begin{equation}
\begin{aligned}
C_{x} &=A_{y} B_{z}-A_{z} B_{y} \\
C_{y} &=A_{z} B_{x}-A_{x} B_{z} \\
C_{z} &=A_{x} B_{y}-A_{y} B_{x}
\end{aligned}
\end{equation}\label{11.4}\]

Notice that once you have the first of these equations, the other two can be obtained by cyclically permuting the indices, i. e., x → y, y → z, and z → x. This is useful as a memory aid.