11.3: Two Particles
( \newcommand{\kernel}{\mathrm{null}\,}\)
Suppose we wish to apply Newton’s second law to two particles considered together as a single system. As we showed previously, only external forces act on the total momentum, ptotal = p1 + p2, of the two particles:
Fexternal =dptotal dt
Let’s write the total non-relativistic momentum of the two particles in a special way:
ptotal =M1v1+M2v2=Mtotal (M1v1+M2v2Mtotal )≡Mtotal Vcm
where Mtotal =M1+M2. The quantity Vcm is the velocity of the center of mass and can be expressed as the time derivative of the position of the center of mass, RCm,
Vcm=dRcmdt
where
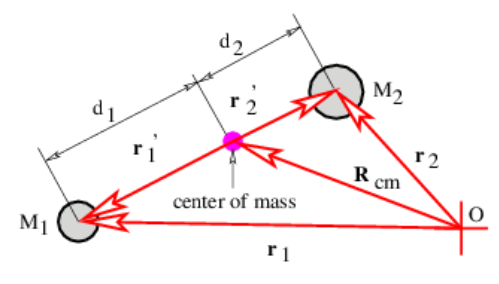
Rcm=M1r1+M2r2Mtotal
We now see how the kinetic energy and the angular momentum of the two particles may be split into two parts, one having to do with the motion of the center of mass of the two particles, the other having to do with the motion of the two particles relative their center of mass. Figure 11.3.5: shows graphically how the vectors \( are defined. These vectors r′1=r1−Rcm and r′2=r2−Rcm represent the positions of the two particles relative to the center of mass. Substitution into equation (???) shows that M1r′1+M2r′2=0. This leads to the conclusion that M1 d1=M2 d2 in Figure 11.3.5:. We also define the velocity of each mass relative to the center of mass as v′1=dr′1/dt and v′2=dr′2/dt, and we therefore have M1v′1+M2v′2=0.
The total kinetic energy is just the sum of the kinetic energies of the two particles, K=M1v21/2+M2v22/2, where v1 and v2 are the magnitudes of the corresponding velocity vectors. Substitution of v1=Vcm+v′1 etc., into the kinetic energy formula and rearranging yields
Ktotal =Ktrans +Kintern =[Mtotal V2cm/2]+[M1v′21/2+M2v′22/2].
Terms like Vcm⋅v′1 cancel out because M1v′1+M2v′2=0.
The first term on the right side of equation (???) in square brackets is the kinetic energy the two particles would have if all of the mass were concentrated at the center of mass. The second term is the kinetic energy computed relative to the motion of the center of mass. The first is called the translational kinetic energy of the system while the second is called the internal kinetic energy.
The angular momentum of the system is just the sum of the angular momenta of the two particles: Ltotal =M1r1×v1+M2r2×v2. By reasoning similar to the case of kinetic energy, we can rewrite this as
Ltotal =Lorb +Lspin =[Mtotal Rcm×Vcm]+[M1r′1×v′1+M2r′2×v′2]
The first term in square brackets on the right is called the orbital angular momentum while the second term is called the spin angular momentum. The former is the angular momentum the system would have if all the mass were concentrated at the center of mass, while the latter is the angular momentum of motion about the center of mass.
Interestingly, the idea of center of mass and the corresponding split of kinetic energy and angular momentum into orbital and spin parts has no useful relativistic generalization. This is due to the factor of γ≡(1−v2/c2)−1/2 in the relativistic definition of momentum, p=mvγ, which means that
dmrdt≠p (relativistic case).


