11.7: Rainbows
( \newcommand{\kernel}{\mathrm{null}\,}\)
Most elementary physics books either do not explain the rainbow at all, or explain it incorrectly (sometimes embarrassingly so). Obviously, it has something to do with the refraction of light by raindrops. We ought to be able to explain it just using Snell’s law and geometrical optics — ray tracing. But it is a little subtle, as you will see.
To begin with, consider the refraction of a narrow ray of light from a spherical drop of water, illustrated in Figure 11.50. The index of refraction of water, n, varies from about 1.332 for red light to about 1.343 for violet light. The ray enters somewhere on the drop, which can parameterize by the angle \theta between the direction of the incoming light and the radius from the center of the drop to the point where the light enters. The angle \theta is also the angle between the light ray and the perpendicular to the surface of the drop, so it is the appropriate to use in Snell’s law. Thus the angle \phi of the refracted ray inside the drop is given by \sin \phi=\frac{1}{n} \sin \theta
or \phi=\sin ^{-1}\left(\frac{\sin \theta}{n}\right)
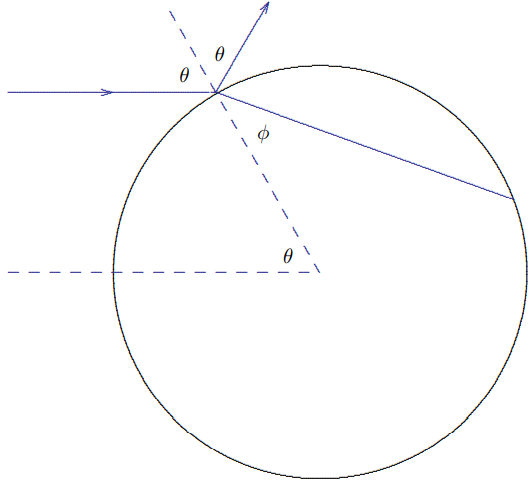
Figure 11.50:
Some of the light is also reflected from the drop. Note that the reflected light is reflected specularly. For \theta = 0, the light is reflected directly backwards. As \theta increases from 0 the reflected ray is rotated counter-clockwise with respect to the incoming ray by an angle \pi-2 \theta until at \theta=\pi / 2 it just kisses the sphere and is not rotated at all.
The important geometrical fact that makes the problem fairly simple is that the angle between the ray and the perpendicular to the surface is the same when it comes out of the drop as when it comes in. Snell’s law works in reverse, and the ray coming out of the drop makes an angle \theta with the perpendicular. As you can see from Figure 11.51, this means
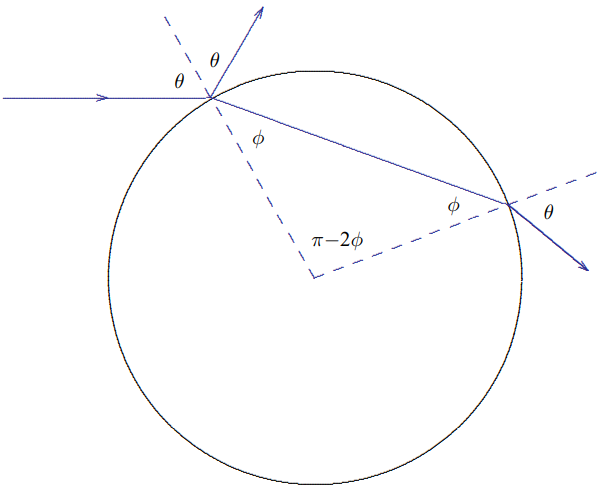
Figure 11.51:
that the refracted ray coming out of the drop This is just a version of the reflected ray in Figure 11.50 rotated by \pi-2 \phi. This means that is it rotated by \theta_{1}=(\pi-2 \phi)-(\pi-2 \theta)=2 \theta-2 \phi
from the original direction of the incoming light.
The trouble with this is that it has nothing to do with the rainbow. The problem is that the direction of the refracted ray is basically forward and it depends on \theta, so that no particular value of \theta is picked out. There are three mysterious things about the rainbow that this effect cannot explain.
- The primary rainbow occurs at a definite angle, and
- the angle is in the backwards direction — at an angle of about 41^{\circ} (about .7 radians) from the incoming light ray — that is rotated by about 2.4 radians from the original direction, and
- there is a second rainbow outside the first in which the colors go in the opposite direction!
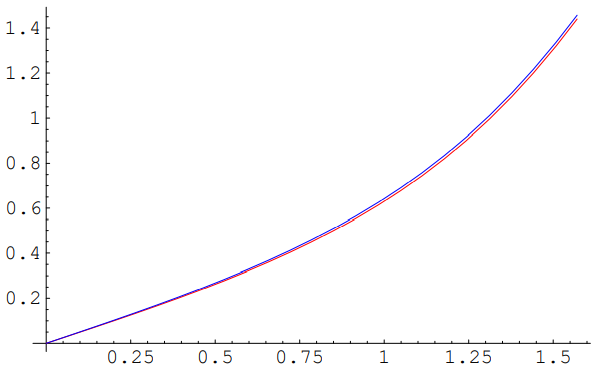
Figure 11.52: Plot of \theta_{1} versus \theta for red light and blue light.
So what does this refraction do? The answer is almost nothing! The refracted ray is spread over a large range of angles, as shown in the graph in Figure 11.52. At any particular outgoing angle, the light from this effect is very faint and hardly noticeable. Not only are the colors not separated very much, but all of them are spread more or less evenly over outgoing angle, so you don’t see any rainbow from this refraction.
So where does the rainbow come from? The answer is that in addition to being refracted from the inside surface of the drop, the ray can also be reflected, and then come out at a still larger angle. The result looks like the picture in Figure 11.53.
Comparing Figure 11.51, Figure 11.53 and equation (11.165), it is clear that for this path the light is rotated by \theta_{2}=2(\pi-2 \phi)-(\pi-2 \theta)=2 \theta+\pi-4 \phi
And now here is the critical point. If we plot this \theta_{2} versus \theta, the graph has a minimum! This is shown in Figure 11.54.
Now the outgoing angle has a minimum for \theta \approx 1.05 (which is the value of \theta illustrated in the diagrams). The outgoing angle \theta_{2} \equiv \theta_{\text {out }} corresponding to this \theta gives the angular position of the rainbow. Here, because \theta_{2} does not change much for a small change in \theta, you see the sum of the refracted light from a range of \thetas around the minimum. The angle is about what we expect, \theta_{\text {out }} \approx \pi-.7, where .7 \text { radians } \approx 41^{\circ} is the angle between a vector from the water drop to the sun and the same drop to your eye, as shown in Figure 11.55. The negative sign in \pi-.7 means that the light has not rotated by a full 180^{\circ}, so the light reaching your eye entered the refracting water drop on the side farther away from you.
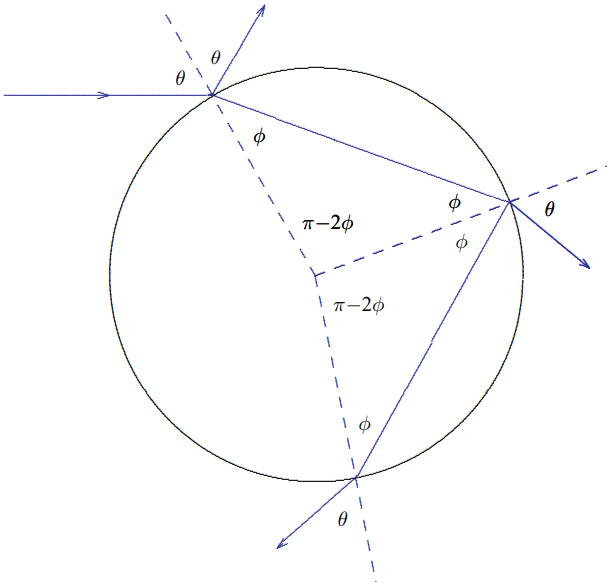
Figure 11.53:
You can also see from the graph in Figure 11.54 that the colors are spread out. The red light is on the outside (farther away from 2 \pi) and the blue light on the inside.
Mathematically, why does the light pile up at the edge? The energy from sunlight falling on a small part of the surface of the water drop between \theta and \theta+d \theta is proportional to I d \theta (there are other factors, like \cos \theta, but they vary slowly, so let’s forget them). The angle of the outgoing ray, \theta_{out} is a function of \theta, and the energy \propto I_{i} d \theta is spread over an angular region between \theta_{out} and \theta_{\text {out }}+d \theta_{\text {out }}. Thus the outgoing intensity is proportional to \begin{aligned} &\text { incoming }\\ &\text { energy between } \propto I_{i} d \theta\\ &\theta \text { and } \theta+d \theta \end{aligned}
\begin{gathered} \text { outgoing } \\ =\quad \text { energy between } \quad \propto I_{o} d \theta_{\text {out }} \\ \theta_{\text {out }} \text { and } \theta_{\text {out }}+d \theta_{\text {out }} \end{gathered}
I_{o} \propto \frac{I_{i} d \theta}{d \theta_{\text {out }}}=\frac{I_{i}}{\frac{d \theta_{\text {out }}}{d \theta}}
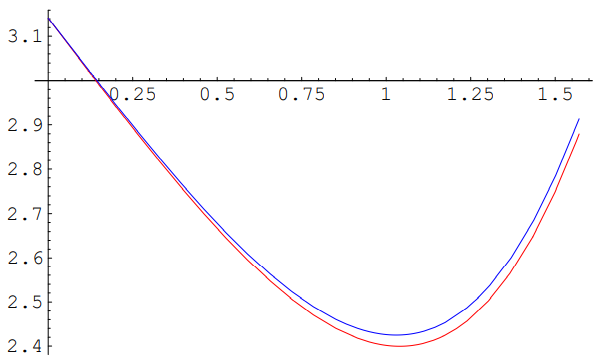
Figure 11.54: Plot of \theta_{2} versus \theta for red light and blue light.
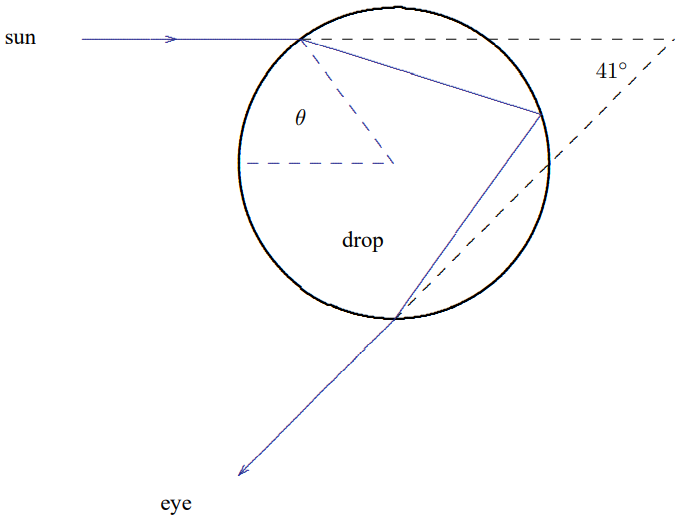
Figure 11.55:
When d \theta_{\text {out }} / d \theta=0, the intensity goes to infinity! The edge is infinitely more bright than the interior. That is why we see it!
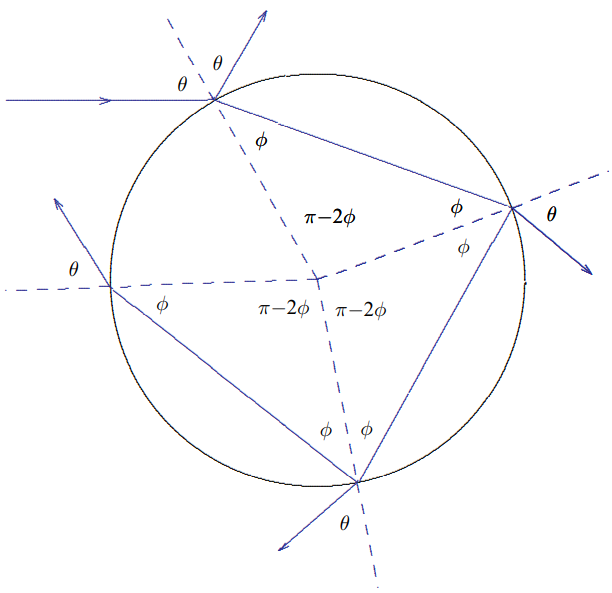
Figure 11.56:
We can now check this picture by seeing how it explains the second rainbow. As you might guess, this comes from yet another reflection, as shown in Figure 11.56.
Now the light ray is rotated by \theta_{3}=3(\pi-2 \phi)-(\pi-2 \theta)=2 \theta+2 \pi-6 \phi
This is shown, along with \theta_{2}, in the plot in Figure 11.57. The minimum of \theta_{3} is the position of the second rainbow. But now because the angle is greater than \pi, the light is reaching your eye from the side of the drop that is closer to you, and it is bending completely around.
This is why the colors are reversed. Again the blue is refracted more, but this time that means that the blue is on the outside, while the red in on the inside.
By accident, the minima for \theta_{2} and \theta_{3} are almost equally (within about .13 radians) displaced from \pi, though on opposite sides. This is why the two rainbows are fairly close together in the sky.
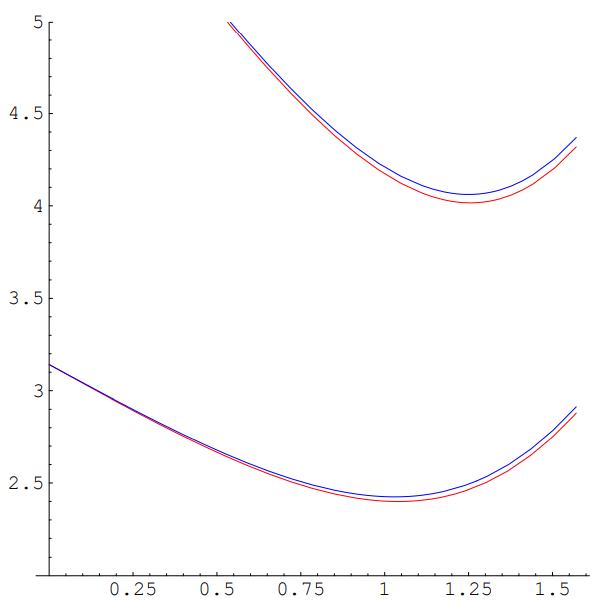
Figure 11.57: Plot of \theta_{2} and \theta_{3} versus \theta for red light and blue light.
Another prediction of this picture that can often be seen is “Alexander’s dark band” that appears between the rainbows. The light that is not concentrated at the minimum value of \theta is spread inside the first rainbow but outside the second rainbow, thus the region between the two rainbows (or outside the first if the second cannot be seen) is darker. If we plot the angular distance away from \pi as a function of the angle at the which the incoming sunlight enters the water drop, the first and second rainbows look like Figure 11.58 (as usual, I have exagerated the difference in index of refraction between red and blue. Here you clearly see that the angle of first rainbow is smaller, and the dark band between the two.

