10.1: Introduction

Introduction to Geometric Optics

In Physics 7C so far we have introduced waves and discussed their interactions. Our model of waves has been so useful because it enabled us to apply the same basic ideas to a wide variety of phenomena: namely waves on ropes, sound waves, light waves and other types of waves. In this chapter we will analyze what happens to waves when they encounter another medium. In such a case two things can happen: part of the wave can bounce back into the original medium which we refer to as reflection, and part of the wave can travel into the next medium, transmission. When a wave travels into a new medium the wave will typically bent or deform in some way, a phenomenon we call refraction.

We can combine these effects of reflecting and refracted waves to make the waves appear as if they are being created at different locations than they actually are. If the waves in question are light waves then this means that we will see images. While most of our examples will involve light waves, it is important to realize that all types of waves will reflect and refract as they pass from one medium to another. For completeness we mention that there are two other methods by which the path of light can be altered: absorption and scattering. We will not discuss these further.

We will focus of reflection and refraction of light waves, since we are interested in understanding how this phenomena leads to images that we can observe. In Physics 7C we have discussed multiple representations of wave phenomena: the wave equation, wavefronts, and rays. The value of using a given representation depends on the phenomena being studied. As we will see in the following sections, the locations and types of images that are formed because of reflection and refraction depend on the direction of light rays. Thus, the most useful wave phenomena in this chapter will be the direction of light waves, which can be described with ray representation introduced in Section 8.2. It is important to keep in mind that rays are not a physical representing of the light wave itself, such as a laser beam of light. All the light rays represent is the direction of the light wave, connecting the original source to the observer. Light rays will be a very useful geometric tool which will enable us to connect the original light source with the interpretation of that source by an observer. It is possible but much more complex to work directly with wavefronts and Huygen's principle to track the motion of waves as it meets different surfaces, but the light rays give us a very powerful and simple tool to use. The analysis of light propagation using rays is known as geometric optics.

How We See Things

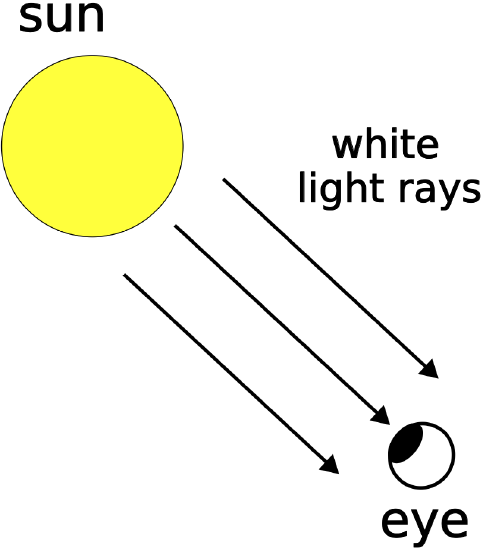
Before going too much further into geometric optics it is worth considering how we see things. First, we must establish that eyes only see light rays that fall on them. A light source emits rays going off in all different directions, and we can see the source if some of those rays enter our eyes. Our brain tells us where the light source is by assuming that the light rays travel in straight lines. An good example of a light source is the sun as shown in the figure below. We can see the sun by interpreting a very small fraction of its rays that enters our eyes.

Figure 10.1.1: Direct Light

Another object such as a tree does not give off its own visible light. We know this because we would not be able to see the tree at night time, without any lights on. On a bright day we see the tree because sunrays hit the tree and reflect from it in many directions, some of which reaching our eyes, as pictured below. The light that is reflected is not the same as the incident light, otherwise everything outside would be the same color as the sun. Instead objects reflect certain colors preferentially, and absorb others. The tree leaves, for example, reflect green strongly and absorb most of the other colors. When sunlight (which is a combination of all the colors) falls on the tree, the green is strongly reflected while colors like red are absorbed. Most of the light that reaches our eyes is green light, this is why the tree appears green. If we can “see” a particular point on the tree, it means some of the rays that reflected from that point enter our eyes. The act of seeing only the top point of the tree is shown below.

Figure 10.1.2: Reflected Light

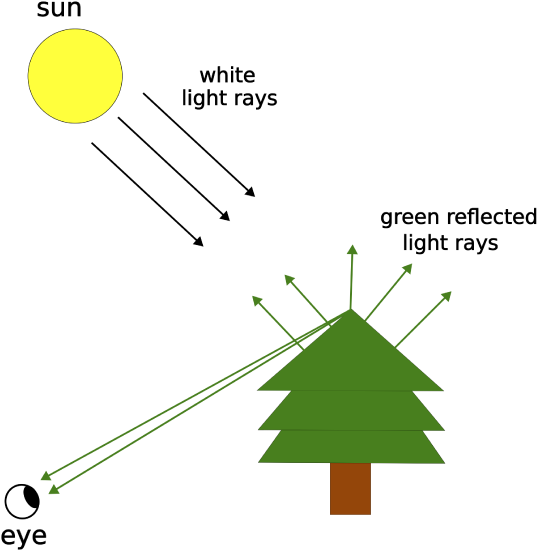
Here multiple rays have been drawn that enter the eye. Our diagram is not meant to suggest that a disproportionate amount of light enters the eye from the top of the tree. We draw a higher density of light rays in this region because we are more interested in light that reaches the eyes than what happens to light going in other directions. If we look at the whole tree, then every point that faces our eye tree that reflects light to our eyes. All points on the tree reflect light in many angles, so our eyes receive light from all points on the tree. The phenomenon of light scattering in all directions when it hits an object is called diffuse reflection.

Seeing Images

Since multiple rays enter our eyes from different locations at slightly different angles, our brain can judge how far away the top of the tree is from us. In doing this, our brain assumes that the light rays traveled to us in a straight line. This approximation is the what is necessary in geometric optics, when trying to analyze what we see from the original source.

These considerations about how we see things raise an interesting possibility. The only information we have access to for sight is the light that reaches our eyes. If the light takes a twisted path to our eyes, then we will judge objects to be at different places, or to be different sizes than they are. This is exactly what happens when we look in a mirror and see an image of ourselves. Our study of optics is essentially the study of how the light given off by objects (whether this light is created by the object or simply reflected) can be manipulated into appearing like it comes from somewhere else. We call this somewhere else an image.

This is illustrated in the figure below. Light rays from some original light source encounter some sort of optical device which consists of a medium with reflects and/or transmits light. This results in outgoing light rays with different direction from the incoming light rays. Those outgoing rays are then viewed by an observer, who interprets those rays as coming from a straight now. If you trace back these outgoing light rays, they all meet at a location which is not the location of the original light source. Thus, what the observer sees is the image of the light source and not the light source itself. 

Figure 10.1.3: Image Formation

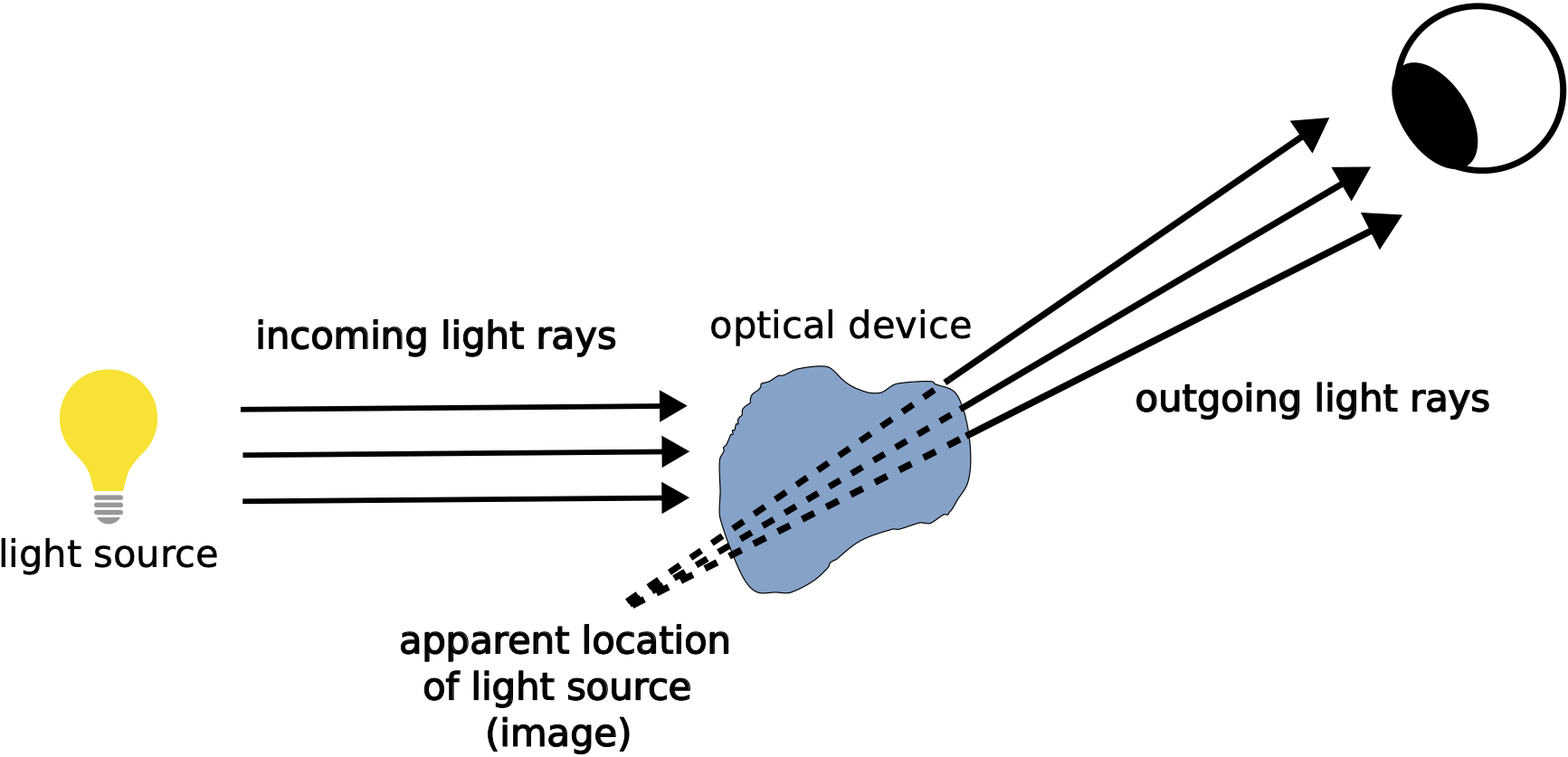
Almost every image used in this section adopts the convention of using solid rays to represent real light rays that actually exists, while using dotted rays to show light rays we interpret to exist. The dotted rays are traced back to the image location, but the solid rays are the actual light rays that we see.