8.8: Standing Waves

Standing Waves Definition

Another important result of wave interference are standing waves. Standing waves are formed when a wave encounters a boundary between two different mediums which allows the wave to reflect. Although one source generated this wave, we now have two traveling waves, one outgoing and one reflected. These two waves will interfere in the same manner as do two waves emerging from two separate sources. However, as we will describe in this section, the unique feature of the combined wave in this scenario, is that it no longer has a distinct direction in which it travels. In other words, although there is time-dependent displacement from equilibrium, the positions of the maximum and minima remain in place, thus, the name "standing wave".

The figure below shows an animation of two counter-propagating waves (blue and red on the top panel) which combine to yield a standing wave (lower wave). The two waves have the same frequency since they originate from the same source, and thus the same wavelength since they travel in the same medium. It it clear from the combined wave below why it is called a "standing wave", since we can no longer assign a direction (right or left) to the motion of the wave. Instead, there are specific locations which are fixed in time, where the combined wave exhibits constructive interference, and other locations where the interference in destructive. The amplitude of the standing waves is double the amplitude of the or the original wave. The frequency with which the standing wave oscillates is the same as the frequency of the source waves. The example depicted below is of a one-dimensional standing wave. Standing waves can also be formed in high-dimensions, but the mathematics become much more complex.

Figure 8.8.1: Standing Waves

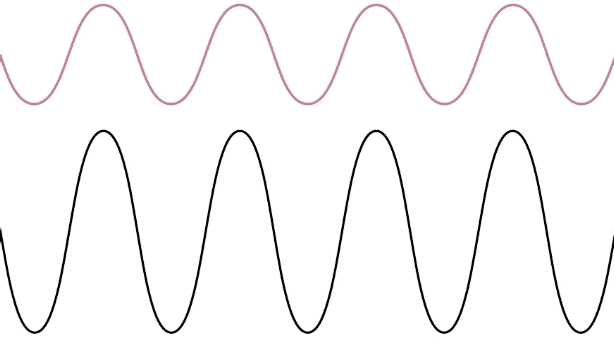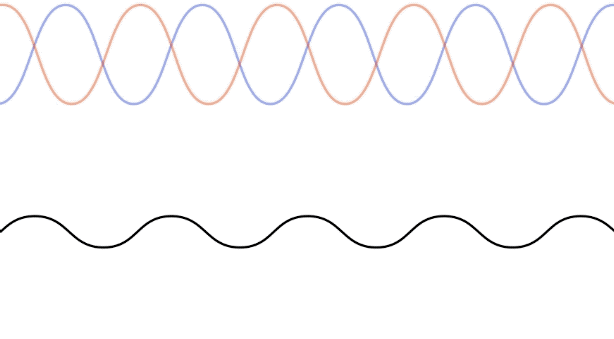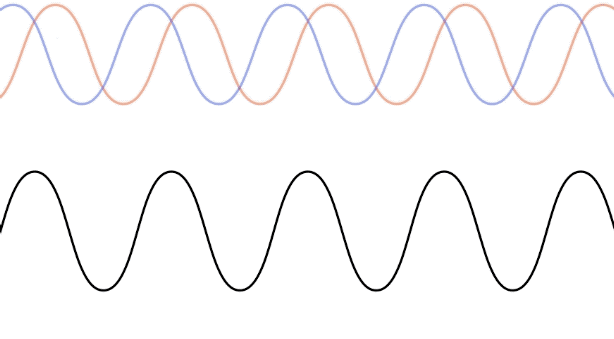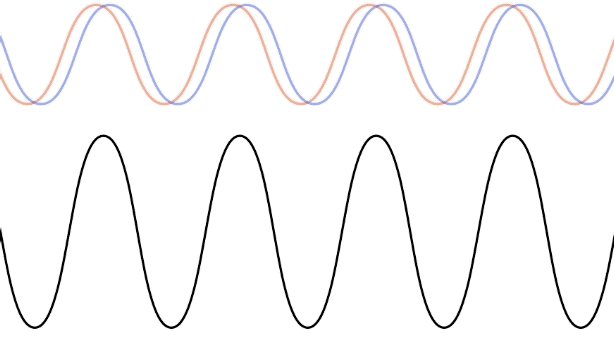
The location of the standing waves where the amplitude is always at equilibrium are called nodes. These are all the locations where the two counter-propagating waves interfere destructively. The distance between two neighboring nodes is half of a wavelength. The location where the wave oscillates away from equilibrium with double the amplitude of the original waves are known at antinodes, where the two waves interfere constructively. Antinodes are also separated by half of a wavelength, and the locations of nodes and antinodes alternate.

Digression: Standing Waves Mathematics

Standing waves result from a right-moving wave interfering with a left-moving one. Recall the wave equation for a right-moving wave is:

\[y_R(x,t)=A\sin\left(\dfrac{2\pi}{T}t-\dfrac{2\pi}{\lambda}x+\phi_1\right)\nonumber\]

And the equation for the left-moving wave is:

\[y_L(x,t)=A\sin\left(\dfrac{2\pi}{T}t+\dfrac{2\pi}{\lambda}x+\phi_2\right)\nonumber\]

One important feature of wave reflections is the change of phase upon reflection. If you watch the animation in the figure above, you can see that at the two ends the outgoing and reflected waves are out of phase. In other words, when the incoming wave hits the fixed end boundary its phase flips by \(\pi\) upon reflection. This results in destructive interference between the outgoing and reflected waves at the location of the fixed ends. This change in phase is intuitive since the fixed ends are held in place and thus are unable to oscillate, making them natural nodes. On the other hand, for free ends there is no change of phase upon reflection, and as we will see later in this section, antinodes are formed at free ends. For now, we will focus our derivation for a system where both ends are fixed.

The difference in phase between the two waves can be written as:

\[\phi_1-\phi_2=\pi\nonumber\]

If we define one fixed end as the origin \(x=0\), we can define \(t=0\) when \(\phi_2=0\) which will result in \(\phi_1=\pi\). Plugging in this result and adding the two equations, we obtain the following equation for the combined wave:

\[y_{tot}(x,t)=y_R(x,t)+y_L(x,t)=A\sin\left(\dfrac{2\pi}{T}t-\dfrac{2\pi}{\lambda}x+\pi\right)+A\sin\left(\dfrac{2\pi}{T}t+\dfrac{2\pi}{\lambda}x\right)\nonumber\]

We can now use the following two identities to help us simplify the above expression:

\[\sin(x+\pi)=-\sin(x)\nonumber\]

\[\sin\alpha-\sin\beta=2\cos\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2}\nonumber\nonumber\]

Applying the above trigonometric properties we get:

\[y_{tot}(x,t)=2A\cos\left(\dfrac{2\pi}{T}t\right)\sin\left(\dfrac{2\pi}{\lambda}x\right)\nonumber\]

You can see from the result above that there the time and the space dependent terms are now separated. The amplitude \(2A\) multiplied by the cosine function represents the time-dependent displacement from equilibrium whose maximum displacement is position-dependent, as dictated by the second sine function. A similar expression for the total wave function can also be obtained for other boundaries, such as free ends.

Activity

Log into a free online graphic calculator: https://www.desmos.com/

Enter the following equation that we obtained above for standing waves: 

\[y_{tot}(x,t)=2A\cos\left(\dfrac{2\pi}{T}t\right)\sin\left(\dfrac{2\pi}{\lambda}x\right)\nonumber\]

You will need to select a value for A, T, and \(\lambda\). 

a) Click on "add slider for t" and press play to watch the animation. Do you observe a traveling wave or a standing wave?

b) To change the locations of the nodes and antinodes which parameter do you need to change? Try it out!

c)To change the frequency with which the antinodes oscillate which parameter do you need to change? Try it out!

d) Now plot the two original wave function from which the standing wave originated:

\[y_R(x,t)=A\sin\left(\dfrac{2\pi}{T}t-\dfrac{2\pi}{\lambda}x+\pi\right)\nonumber\]

\[y_L(x,t)=A\sin\left(\dfrac{2\pi}{T}t+\dfrac{2\pi}{\lambda}x\right)\nonumber\]

Display all three functions. Instead of running the animation, drag the "t slider" and observe the overlap of the two wave at the nodes and antinodes of the standing waves. From your observations, what type of interference do you see at the nodes and at the antinodes?

Standing Waves Harmonics

When standing waves are formed due to boundaries enforced on a medium through which the waves propagate, such as a string with two ends fixed, we have learned that the two ends have to be nodes. This means that only specific wavelengths can fit on the string of a fixed length, with nodes always at the ends, and otherwise nodes and antinodes alternating on the length of the string. This is demonstrated in the figure below. The longest possible wavelength that can fit is one where there is one antinode between the nodes. The dashed waved shown represents the motion of the antinode which oscillates from the maximum (solid line) to the minimum (dashed line). The wavelength of this standing wave can be expressed in terms of the length of the string. Since half a cycle is displayed on the string, \(\lambda=2L\), where \(L\) is the length of the string when its at equilibrium.

Figure 8.8.2: Harmonics for Two Fixed Ends

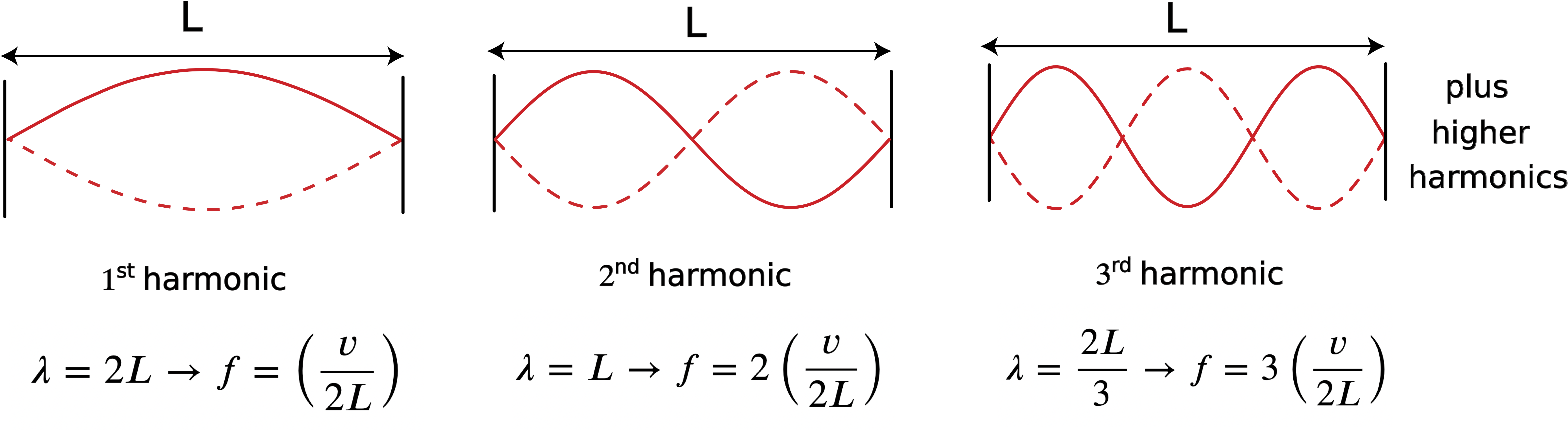
The next longest wavelength is shown in the middle panel of the figure, with two antinodes and one node between the two ends. In this case exactly one wavelength fits on the entire string such that, \(\lambda=L\). The get the next longest wavelength we add one node and one antinode, such that one and a half wavelengths fit on the string, or \(\lambda=2/3L\). Thus, every time the wavelength is shortened, and extra half of a wavelength fits between the two ends. This gives a general relationship for possible wavelengths on a string of length \(L\):

\[\lambda_n=\dfrac{2L}{n};~n=1,2,3,...\label{L-fixed}\]

where \(n\) is a positive integer. Each wavelength then corresponds to a specific frequency. These discrete allowed frequencies are known as harmonics. The first three harmonics are shown in Figure 8.8.2. The first harmonic is also often called the fundamental harmonic. We can express all the possible frequencies in terms of the frequency of the fundamental harmonic, using the wavelengths in Equation \ref{L-fixed}:

\[f_n=\dfrac{v}{\lambda}=\left(\dfrac{v}{2L}\right)n=f_1n;~n=1,2,3,...\label{f-fixed}\]

where \(f_1=v/2L\) is the fundamental frequency. Thus, we can think of frequency of \(n^{th}\) harmonic, as the \(n^{th}\) multiple of the fundamental harmonic.

Alert

For traveling waves we learned that frequency is source dependent and wavelength depends on both the frequency and the medium which determines the speed. These concepts no longer apply for standing waves. In this case, the geometry of the medium determines the allowed wavelengths, which as a result determine the allowed frequencies, which depend on both the wavelength and the medium.

We will now look at all the different types of boundaries that are possible for a wave on a string. Below are the first three harmonics for a standing wave where both ends are free. Free ends results in antinodes at the edges. This situation is not possible for a string which requires tension for waves to propagate, but would work for a rigid system. An example of such a system in shown in Video 8.8.1 below. 

Figure 8.8.3: Harmonics for Two Free Ends

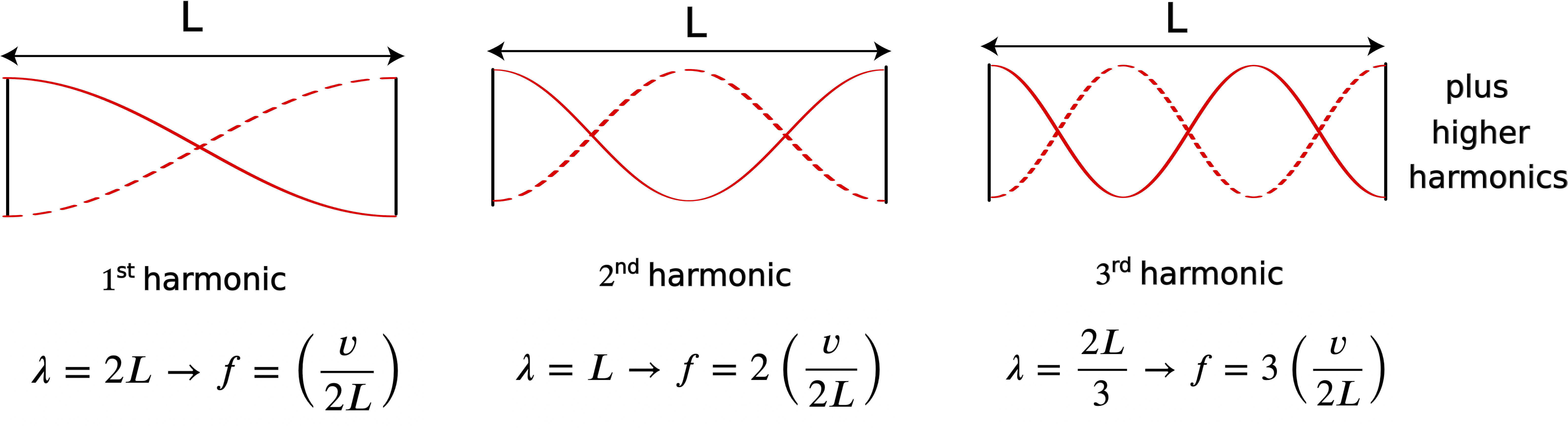
In this case, the longest wavelength has one node between that two antinodes at the ends. The next longest wavelength has one additional node and antinode between the two ends, and so on. Although, the structure of theses standing waves is different from those in Figure 8.8.2, it results in the same relationship between wavelength and the length of the system. Thus, Equation \ref{f-fixed} for the frequencies of the different harmonics applies for this scenario of two free ends.

The last scenario of one fixed and one free end is shown in the figure below. This scenario is also demonstrated in Video 8.8.1. In this case, the longest wavelength corresponds to a node at one end and an antinode at the other one, which is one quarter of a wavelength that fits along the length of the system. Shortening the wavelength with each higher harmonic results in an addition of one node and one antinode. The first three harmonics with their corresponding wavelengths and frequencies are shown below.

Figure 8.8.4: Harmonics for One Fixed One Free End

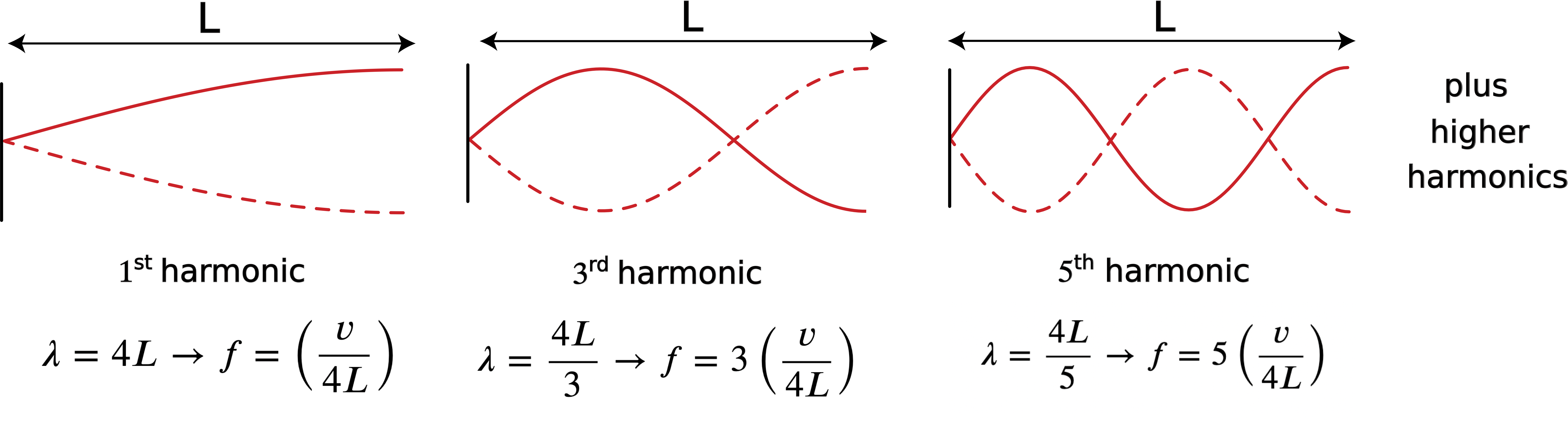
The general conditions for the possible wavelengths for a system with one fixed and one free end can be written as:

\[\lambda_n=\dfrac{4L}{n};~n=1,3,5,...\label{L-fixed-free}\]

where in this case, \(n\) is a positive odd integer. As for the two previous cases, fixed-fixed and free-free ends, frequency of each higher harmonic can be written as a multiple of the frequency of the fundamental harmonic:

\[f_n=\dfrac{v}{\lambda}=\left(\dfrac{v}{4L}\right)n=f_1n;~n=1,3,5,...\label{f-fixed-free}\]

where \(f_1=v/4L\) is the fundamental frequency for a system with one fixed and one free end. A demonstration of standing waves with various boundary conditions is shown in the video below. The medium used to generate what are called "torsion waves" are multiple rods which are attached together by a central rod allowing the wave to propagate along the system.

Video 8.8.1: System with Two Free Ends and one Free and one Fixed End                

In addition to strings, air pressure standing waves can be formed inside cavities or pipes. When air flow is forced through a cavity, reflections at the boundaries of the cavity and the atmosphere creates pressure standing waves, in a similar manner as they are created on strings. 

Alert

Recall, for sound waves we express wave displacement in terms of pressure. At an open end of a container (such as a pipe) where a sound standing wave is formed, the pressure is fixed at atmospheric pressure since that end is in contact with the atmosphere. Therefore, the open end of a pipe is a node. At a closed end, the pressure is able to vary as the pressure waves reflected from the hard surface causing periodic compression and rarefactions. As a result, the closed end of a pipe is an antinode. This is an important feature to keep in mind with sound standing waves, since it might be confused with a free end on a rope being a node, while the fixed end as an anti-node. To summarize, for standing waves on strings: fixed end is a node and a free end is an antinode; for sound standing waves inside pipes: open end is a node and a closed end is an antinode.

The sounds from musical instruments are generated due to standing waves formed on strings for string instruments and air standing waves formed inside wind instruments. If you try to vibrate string attached at both ends at a particular frequency, you may or may not be successful depending on the frequency you choose. At most frequencies, the wave you start will travel to the one end intact, but upon reaching it the shape of the wave distorts and overall the string no longer appears to carry a wave. Nowhere will the string displace very far from equilibrium. In a standard scenario, such as plucking a guitar string, all the harmonics are excited, with the first or the fundamental being the dominant one. Wind instruments create standing waves in cavities. A flute, for example, is a pipe with both ends open, while a clarinet can be modeled by a pipe with one open end and one closed end, since the mouth covers one end of the instrument.

Example \(\PageIndex{1}\)

You are conducting experiments with a torsion wave which is shown in the video above. The video demonstrate how you can have either a free or a fixed end on a torsion wave.

a) You start with both ends fixed. You move one rod at the very edge to generate a pulse, and measure that it takes the wave pulse 0.5 sec to get to the other end of the apparatus. Then you discover that oscillating the rod at a rate of four oscillations per second generates a standing wave pattern. Draw the standing wave pattern that is formed.  

b) Now you change the set up such that one end becomes free, while the other end is still fixed in space. You continue to oscillate the rod at the same frequency as before.  Explain what happens to the standing wave pattern you observed in a).

Solution

a) For 2 fixed ends the possible wavelengths are the allowed frequencies are:

\[f=\dfrac{vn}{2L}\nonumber\]

To find the speed of the wave we use the information given: it takes a wave pulse 0.5 sec to travel the length of the system L, so the speed of the wave in this medium is:

\[v=\dfrac{\text{distance}}{\text{time}}=\dfrac{L}{ 0.5 s}\nonumber\]

To find the standing wave pattern, we need to know the harmonic. The frequency with which you move the rod is 4Hz. Solving for n: 

\[n=\dfrac{2Lf}{v}=\dfrac{2L\times 4 Hz\times 0.5 s}{L}=2\times 4 Hz\times 0.5 s = 4 \nonumber\]

Standing wave in the fourth harmonic has 4 antinodes. The diagram is shown below.

b) For one fixed and one free end the possible frequencies are:

\[f=\dfrac{vn}{4L}=\dfrac{v}{4L},\dfrac{3v}{4L}, \dfrac{5v}{4L}, ...\nonumber\]

  For two fixed ends:   

\[f=\dfrac{vn}{2L}=\dfrac{vn}{2L}=\dfrac{v}{2L},\dfrac{2v}{2L},\dfrac{3v}{2L}, ...\nonumber\]

The frequencies can never be the same for for the same length and speed, since the numerators are odd for free-fixed ends and even for fixed-fixed ends (if you make all the denominators 4L).  Since 4 Hz formed a standing wave pattern when both ends were fixed, there will be no standing waves when one end is free. Or you can solve directly for n for the when one end is fixed and one is free:

\[n=\dfrac{4Lf}{v}=4\times 4 Hz\times 0.5 s=8\]

Since n is not an even integer, a standing wave is not possible since by definition the integer must be odd for one fixed and one free end.

Example \(\PageIndex{2}\)

A standing wave in a pipe with both ends open is detected when the sound produced by striking a tuning fork is greatly amplified, a. The set-up is shown below. Let's assume that the length of the pipe is 0.5m, and the speed of sound in air is 340m/s.

a) Different tuning forks of increasing frequency are used until the first resonance (standing wave) is heard in the pipe with both ends open. Then, more tuning forks are used with increasing frequencies until a tuning fork is found such that a second resonance is heard.  Plot the standing wave pattern (using displacement in pressure) produced by the final tuning fork. Calculate the frequency of this tuning fork.

b) One of the ends is closed with a piston which is initially positioned on the right side of the pipe, such that the length of the pipe is still 0.5m. Explain what happens with the resonant sound, if the same turning fork as found in a) is used?

c) The piston shown above is free to move, thus you are able to shorten the length of the pipe.  Find the longest length of pipe you can have in order to generate a standing wave pattern using the same tuning fork as in part a).  Show the length calculation and plot the resulting standing wave pattern below.

Solution

a) Second resonance implies second harmonic n=2.  At both ends of the pipe there must be nodes, since the pipe is open, thus the pressure is atmospheric. Using the equation below for wavelength, and solving for frequency when n=2:

\[f=\dfrac{vn}{2L}=\dfrac{2\times 340 m/s}{2\times 0.5 m}=680 Hz\nonumber\]

The second harmonic is drawn below.

b) A piston placed at the edge of one end changes the system to one open end and one closed end. The open end is a node with the pressure kept fixed by atmospheric pressure, while the other end is an anti-node where the pressure can vary from maximum to minimum as the sound waves collides with the piston resulting in periodic rarefactions and compressions upon reflections.The allowed frequencies a system of a node at one end and an anti-node at the other end are:

\[f=\dfrac{vn}{4L}\nonumber\]

where \(n\) is an odd integer.

Using the same frequency as in a) and solving for n we get:

\[n=\dfrac{4Lf}{v}=\dfrac{4\times 0.5m\times 680Hz}{340 m/s}=4\nonumber\]

However, n must be an odd integer. Thus, no standing wave is possible with this frequency, so no resonance will be heard.

c) Now the length can be adjusted, so we can solve for \(L\) such that the odd harmonics are satisfied for a frequency of 680 Hz. Solving the equation in part b) for L:

\[L=\dfrac{vn}{4f}=\dfrac{340 m/s}{4\times 680Hz}n=0.125m,0.375m,0.625m,...\nonumber\]

Since the length of the pipe is 0.5 m, the longest effective length that can be made by shortening the pipe the the piston is 0.375m. This length corresponds to n=3 harmonic which is shown below.